
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Види середніх величин та способи їх обрахування.
Найбільш простим видом середніх величин є середньоарифметична проста:
 ,
,
де n – кількість одиниць сукупності,
x – варіруюча ознака.
Вона застосовується в тому випадку, коли у нас варіруюча арифметична ознака має різні значення, і є незгруповані дані.
Якщо ж ми маємо згруповані дані, або варіруюча ознака зустрічається декілька раз, то застосовується середня арифметична зважена.
 ,
,
де x – варіруюча ознака,
f – абсолютна кількість повторення варіруючої ознаки.
Середня гармонічна (гармонійна).
| Фірми | Вихідні дані | Розрахункові дані | |
| Середня зарплата на 1 робітника, грн. | Фонд заробітної плати, тис. грн. | Середня кількість робітників, чол. | |
| Разом |
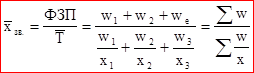
де x – середня кількість робітників, w – середня заробітна плата.
Середня гармонійна зважена застосовується тоді, коли ми маємо загальний обсяг і індивідуальні значення, але не маємо кількості індивідуальних значень.
Приклад. Використання середньої гармонічної. Автомобіль проїхав певну відстань (візьмемо її за 1) зі швидкістю 40 км/год. Назад він повертався зі швидкістю 60 км/год. Яка ж його середня швидкість?
Для розрахунку використаємо середню гармонічну просту:
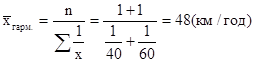
Середня гармонічна – це обернена величина до середньої арифметичної, обчислена з обернених величин осереднюваних варіруючих ознак.

Середні поділяються на 2 великі класи: структурні і степеневі (сюди належать середня гармонічна, середня геометрична, середня квадратична, середня прогресивна тощо).
Середня геометрична розраховується за формулою: 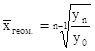
Приклад. Використання середньої арифметичної для розрахунку недискретного ряду.
| Групування робітників за розміром зарплати | Кількість робітників | Фонд заробітної плати |
| До 100 | ||
| 100 – 120 | ||
| 120 – 140 | ||
| 140 – 160 | ||
| Понад 160 | ||
| Разом |
Необхідно знайти середню заробітну плату робітників.
Перш за все ми повинні закрити верхні і нижні границі. Оскільки величина інтервалу в подальших групах дорівнює 20 од., перший інтервал записуємо "80 – 100", останній – "160-180". Потім знайдемо середину інтервалу:
| Групування робітників за розміром зарплати (x) | Кількість робітників (f) | Середини інтервалу | Фонд заробітної плати |
| До 100 | |||
| 100 – 120 | |||
| 120 – 140 | |||
| 140 – 160 | |||
| Понад 160 | |||
| Разом |
Тоді середня арифметична зважена:

Читайте також:
- Абсолютна величина числа позначається символом .
- Абсолютні і відносні величини
- Абсолютні і відносні статистичні величини
- Абсолютні, відносні та середні величини.
- Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
- Багатовимірні випадкові величини. Система двох випадкових величин
- Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
- Біологічні способи лікування ран.
- Валютний курс і способи його визначення
- Варіанти і способи вимірювань характеристик телефонних каналів
- Векторні і скалярні величини
- Векторні і скалярні величини
| <== попередня сторінка | | | наступна сторінка ==> |
| Середні величини. | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |