• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Похідна функції за напрямком. Градієнт функції

Похідною функції 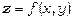в точці М(х,у) за напрямком вектора 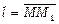називається границя

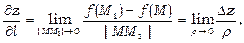де .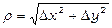

Якщо функція 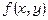диференційовна, то похідна за даним напрямком обчислюється за формулою

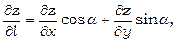
де 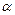- кут, утворений вектором l та віссю Ох.

У випадку функції трьох змінних 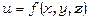похідна за даним напрямком визначається аналогічно. Відповідна формула має вигляд

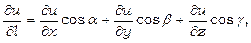
де 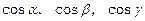- направляючі косинуси вектора l.

Градієнтом функції 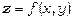в точці М(х,у) називається вектор з початком у точці М, що має своїми координатами частинні похідні функції z:

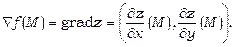
Градієнт вказує напрямок найшвидшого зростання функції в даній точці. Похідна 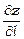в напрямку градієнта має найбільше значення:

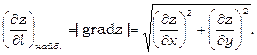
У випадку функції u=f(x, y, z) градієнт функції дорівнює

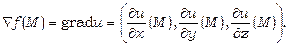
Читайте також:

1. Адвокатура в Україні: основні завдання і функції
2. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
3. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
4. Аналіз коефіцієнтів цільової функції
5. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
6. Асимптоти графіка функції
7. Базальні ядра, їх функції, симптоми ураження
8. Базові функції, логічні функції
9. Банки як провідні суб’єкти фінансового посередництва. Функції банків.
10. Банківська система та її основні функції
11. Банківська система та її структура. Функції Центрального банку.
12. Банківська система: сутність, принципи побудови та функції. особливості побудови банківської системи в Україн

Переглядів: 7737