• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Внутрішня енергія і теплоємність ідеального газу

Теплоємністю якого-небудь тіла називають величину, рівна кількості теплоти, яку потрібно надати тілу, щоб підвищити його температуру на один кельвін. Аналітично це визначення записується в такий спосіб:

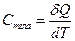, (21.3)

де 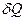- кількість теплоти, надання якої підвищує температуру тіла на 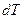. Теплоємність тіла вимірюється в Дж/К.

Теплоємність одиниці маси речовини, яку називають питомою теплоємністю, позначають малою літерою . Вимірюється вона в Дж/(кг·К).

У фізиці воліють користатися теплоємністю моля речовини, яку називають молярною теплоємністю. Вимірюється вона в Дж/(моль·К). Позначають цю теплоємність прописною буквою .

Питома і молярна теплоємності пов'язані співвідношенням

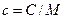(21.4)

де 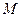– молярна маса.

Теплоємність залежить від умов, при яких відбувається нагрівання тіла. Найбільший інтерес являє собою теплоємність для випадків, коли нагрівання відбувається при сталому об’ємі чи при сталому тиску. У першому випадку ми маємо справу з теплоємністю при сталому об’ємі , у другому – з теплоємністю при сталому тиску .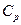

Якщо нагрівання відбувається при сталому об’ємі, то тіло не виконує роботи над зовнішніми тілами і, отже, уся теплота йде на приріст внутрішньої енергії тіла: 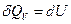(див. формулу (1.2)). Звідси випливає, що молярна теплоємність будь-якої речовини при сталому об’ємі дорівнює

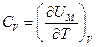(21.5)

Теплоємність при сталому тиску 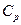більша, ніж , тому що при тіло, що нагрівається, розширюється і частина наданої теплоти витрачається на здійснення роботи над зовнішніми тілами.

Дослідним шляхом встановлено, що у газів, близьких по своїх властивостях до ідеального газу, теплоємність при сталому об’ємі в широких температурних інтервалах практично не залежить від температури: .

Відповідно до формули (21.5)

.

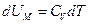Проінтегрувавши це співвідношення, отримаємо вираз для внутрішньої енергії моля ідеального газу

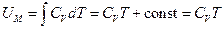(21.6)

Внутрішня енергія визначається з точністю до довільної сталої. Тому константу у виразі для можна відкинути. Внутрішня енергія – величина адитивна. Отже, внутрішня енергія маси газу буде дорівнювати

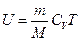(21.7)

Запишемо рівняння першого закону термодинаміки для моля газу, підставивши і припустивши, що теплота надається газу при постійному тиску:

,

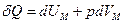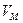( – об’єм 1 моля). Поділивши цей вираз на приріст 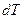, що отримує температура при наданні газу теплоти 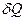, прийдемо до формули для молярної теплоємності газу при сталому тиску:

( ).

Відповідно до формули (21.5) доданок 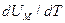дорівнює молярній теплоємності при сталому об’ємі. Отримуємо

(21.8)

Ми не робили ніяких припущень про властивості газу, тому формула (2.6) справедлива для будь-яких газів. Тепер припустимо, що газ ідеальний. Відповідно до рівняння стану ідеального газу (для одного моля ) . Продиференціюємо цей вираз по 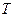в припущенні, що , отримаємо

(21.9)

Підстановка цього значення похідної приводить до співвідношення

, (21.10)

яке називається рівнянням Майєра. Таким чином, робота, виконана молем ідеального газу при підвищенні його температури на один кельвін при сталому тиску, дорівнює газовій сталій .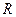

Підкреслимо, що співвідношення (21.10) справедливо лише для ідеального газу.

Відношення теплоємностей

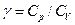(21.11)

називається показником адіабати і являє собою характерну для кожного газу величину. Молекулярно-кінетична теорія дозволяє встановити зв'язок між теплоємністю ідеального газу і кількістю ступенів вільності молекули. Внутрішню енергію моля ідеального газу можна знайти, помноживши середню енергію однієї молекули 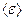на сталу Авогадро . Середня енергія молекули дорівнює 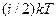. Отже,

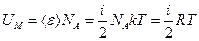(21.12)

Порівняння виразів (21.6) і (21.12) дає для молярної теплоємності ідеального газу при сталому об’ємі формулу

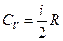. (21.13)

Відповідно до закону Майєра

(21.14)

З формул (21.10) і (21.14) випливає, що

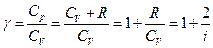(21.15)

Читайте також:

1. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
2. Важливим параметром конденсаторів є пробивна напруга конденсатора. Чим вона більша, тим надійніший конденсатор, тим більша енергія може сконцентруватись на ньому.
3. Власна енергія зарядів.
4. Внутрішня будова довгастого мозку
5. Внутрішня будова Землі
6. Внутрішня будова мосту
7. Внутрішня будова спинного мозку
8. Внутрішня будова спинного мозку
9. Внутрішня будова твердої речовини
10. Внутрішня будова.
11. Внутрішня громадськість та імідж організації.

Переглядів: 4097