
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Операції над множинами та їхні властивості
Для множин можна ввести ряд операцій (теоретико-множинних операцій), результатом виконання яких будуть також множини. За допомогою цих операцій можна конструювати із заданих множин нові множини.
Нехай A і B – деякі множини.
1.1.6.1. Означення 1.1.4. Об’єднанням множин A і B (позначають AÈB ) називають множину тих елементів, які належать хоча б одній з множин A чи B. Символічно операція об’єднання множин записується так
AÈB = {x | xÎA або xÎB} або xÎAÈB Û 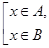 .
.
Наприклад, {a,b,c}È{a,c,d,e}={a,b,c,d,e}.
Властивості об¢єднання множин:
1) комутативність: AÈB = BÈA;
2) асоціативність: (AÈB)ÈC = AÈ(BÈC);
3) ідемпотентність AÈA = A;
4) AÈÆ = A;
5) AÈЕ = Е.
1.1.6.2. Означення 1.1.5. Перетином (перерізом) множин A і B (позначають A Ç B ) називають множину, що складається з тих і тільки тих елементів, які належать множинам A і B одночасно. Тобто
AÇB = {x | xÎA і xÎB} або xÎAÇB Û  .
.
Наприклад, {a,b,c}Ç{a,c,d,e} = {a,c},
{a,b,c}Ç{d,e} = Æ.
Кажуть, що множини A і B не перетинаються, якщо AÇB = Æ.
Операції об’єднання та перетину множин можуть бути поширені на випадок довільної сукупності множин {Ai | iÎ N }. Так об’єднання множин Ai (записується 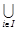 Ai ) складається з тих елементів, які належать хоча б одній з множин Ai даної сукупності. А перетин множин A (записується
Ai ) складається з тих елементів, які належать хоча б одній з множин Ai даної сукупності. А перетин множин A (записується 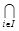 Ai) містить тільки ті елементи, які одночасно належать кожній з множин Ai.
Ai) містить тільки ті елементи, які одночасно належать кожній з множин Ai.
Властивості перерізу множин:
1) комутативність: AÇB = BÇA;
2) асоціативність: (AÇB)ÇC = AÇ(BÇC);
3) дистрибутивність операції Ç відносно операції È: AÇ(BÈC)=(AÇB)È(AÇC);
4) дистрибутивність операції È відносно операції Ç: AÈ(BÇC)=(AÈB)Ç(AÈC);
5) ідемподентність: AÇA = A;
6) AÇÆ = Æ;
7) AÇЕ = A;
8)  AÇ(AÈB) = A;
AÇ(AÈB) = A;
9) AÈ(AÇB) = A.
1.1.6.3. Означення 1.1.6. Різницею множин A і B (записується A\B ) називають множину тих елементів, які належать множині A і не належать множині B. Отже,
A \ B = { x | xÎA і xÏB} або xÎA \ B Û 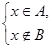 .
.
Наприклад, {a,b,c} \ {a,d,c} = {b},
Z \ Z+=Z–,
{a,b} \ {a,b,c,d} = Æ.
Властивості різниці множин:
1) А \ А=Æ;
2) А \Æ=А;
3) А \ Е=Æ;
4) А \ В ¹ В \ А – різниця не комутативна;
5) (А \ В) \ С ¹ А \ (В \ С) – різниця не асоціативна;
6) (B È C) \ А = (В \ А) È (С \ А) – правий закон дистрибутивності операції \ відносно операції È;
7) (B Ç C) \ А = (В \ А) Ç (С \ А) – правий закон дистрибутивності операції \ відносно операції Ç.
1.1.6.4. Означення 1.1.7. Симетричною різницею множин A і B (записують ADB, AÅB або A¸B ) називають множину, що складається з усіх елементів множини A, які не містяться в B, а також усіх елементів множини B, які не містяться в A. Тобто
AÅB = { x | ( xÎA і xÏB ) або ( xÎB і xÏA )} або xÎAÅB Û 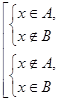 .
.
Наприклад, {a,b,c}Å{a,c,d,e} = {b,d,e},
{a,b}Å {a,b} = Æ.
Властивості симетричної різниці:
1) комутативність: AÅB = BÅA;
2) асоціативність: (AÅB)ÅC = AÅ(BÅC);
3) дистрибутивність операції Ç відносно операції Å: AÇ(BÅC)=(AÇB)Å(AÇC);
4) AÅA = Æ;
5) AÅÆ = А;
6) AÅB = (A \ В) È (В \ А).
Введені теоретико-множинні операції можна проілюструвати діаграмою (рис.1.1).
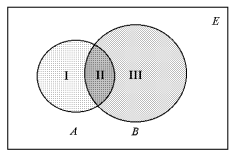
Рис. 1.1.
Тут множини A і B – це множини точок двох кругів.
Тоді AÈB – складається з точок областей І, ІІ, ІІІ,
AÇB – це область ІІ,
A \ B – область І,
B \ A – область ІІІ,
AÅB – області І і ІІІ.
1.1.6.5. Означення 1.1.8. Якщо зафіксована універсальна множина E, то доповненням множини A (яке є підмножиною універсальної множини E ) називають множину всіх елементів універсальної множини, які не належать множині A. Записують 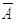 .
.
Тобто
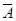 = { x | xÎE і xÏA } або xÎ
= { x | xÎE і xÏA } або xÎ 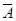 Û xÏA.
Û xÏA.
Неважко помітити, що 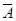 = E \ A.
= E \ A.
Наприклад, якщо за універсальну множину прийняти множину N всіх натуральних чисел, то доповненням 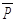 множини P всіх парних натуральних чисел буде множина всіх непарних натуральних чисел.
множини P всіх парних натуральних чисел буде множина всіх непарних натуральних чисел.
Властивості доповнення:
1)  ;
;
2) 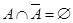 ;
;
3) 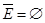 ;
;
4) 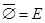 ;
;
5) інволютивність: 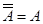 ;
;
6)  ;
;
7) якщо А=В, то 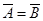 ;
;
8) якщо 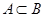 , то
, то  ;
;
9) правила (закони) де Моргана  =
= 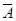 Ç
Ç 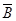 ;
; 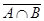 =
= 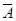 È
È 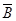 Зазначимо, що правила де Моргана припускають узагальнення для сукупності множин:
Зазначимо, що правила де Моргана припускають узагальнення для сукупності множин:
 ;
; 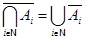 .
.
Приклад. Покажемо істинність однієї з наведених тотожностей – правила де Моргана.
 =
= 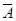 Ç
Ç 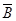 .
.
Доведемо спочатку, що  Í
Í 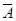 Ç
Ç 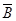 .
.
Нехай елемент xÎ  , тоді xÎE \ (A È B), тобто xÏA і xÏB, звідси xÎ
, тоді xÎE \ (A È B), тобто xÏA і xÏB, звідси xÎ 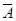 і xÎ
і xÎ 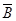 , отже, xÎ
, отже, xÎ 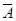 Ç
Ç 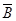 . Отже, за означенням підмножин:
. Отже, за означенням підмножин:  Í
Í 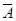 Ç
Ç 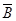 .
.
Доведемо обернене включення: 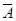 Ç
Ç 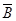 Í
Í  .
.
Припустимо xÎ 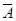 Ç
Ç 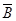 , це означає, що xÎ
, це означає, що xÎ 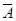 і xÎ
і xÎ 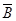 , тобто xÏA і xÏB, тому xÏAÈB, отже xÎ
, тобто xÏA і xÏB, тому xÏAÈB, отже xÎ  . Зі справедливості обох включень
. Зі справедливості обох включень  Í
Í 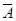 Ç
Ç 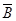 і
і 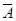 Ç
Ç 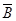 Í
Í  за законом антисиметричності для підмножин випливає істинність рівності
за законом антисиметричності для підмножин випливає істинність рівності  =
= 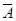 Ç
Ç 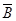 .
.
Твердження доведено. <
Аналогічно можуть бути доведені всі інші наведені теоретико-множинні тотожності. Ці тотожності дають змогу спрощувати різні складні вирази над множинами.
Приклад. (AÇBÇCÇ  )È(
)È( 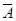 ÇC)È(
ÇC)È( 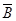 ÇC)È(CÇD) = (AÇBÇCÇ
ÇC)È(CÇD) = (AÇBÇCÇ  )È((
)È(( 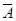 È
È 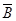 È D)ÇC) = = ((AÇBÇ
È D)ÇC) = = ((AÇBÇ  ) È (
) È ( 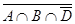 ))ÇC = EÇC = C. <
))ÇC = EÇC = C. <
Читайте також:
- OПТИЧНІ ВЛАСТИВОСТІ КОЛОЇДНИХ СИСТЕМ
- А) Товар і його властивості.
- Аеродинамічні властивості колісної машини
- Активні операції банків
- Активні операції банків з цінними паперами
- Активні операції комерційних банків
- Активні операції центральних банків.
- Алгебраїчні операції
- Алкани (насичені вуглеводні). Хімічні властивості алканів
- Алкани, їх хімічні властивості.
- Алкени. Хімічні властивості
- Алкіни. Хімічні властивості
| <== попередня сторінка | | | наступна сторінка ==> |
| Підмножини. Універсальна множина. | | | Потужність множин |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |