Системи та сукупності нерівностей з однією змінною та способи їх розв’язування. Нерівності та системи нерівностей з двома змінними, графічний спосіб їх розв’язування.

Доведення.

Доведення теореми складатиметься з двох частин. У першій частині доведемо, що кожен розв’язок нерівності (І) є розв’язком нерівності (IV). Нехай Т₁ÌХ - це множина розв’язків нерівності (І), а Т₄ÌХ - це множина розв’язків нерівності (IV). Виберемо в множині Т₁ довільне х₀ÎТ₁ і підставимо у нерівність (І). Після цього одержимо істинну числову нерівність f(х₀)>g(х₀). Підставивши х₀ у вираз j(х), ми одержимо числовий вираз j(х₀), який набуває від’ємних значень. Помножимо обидві частини істинної числової нерівності f(х₀)>g(х₀) на вираз j(х₀), що приймає лише від’ємних значень. Тоді, згідно властивостей істинних числових нерівностей, нерівність f(х₀)·j(х₀)<g(х₀)·j(х₀) буде істинною числовою нерівністю. Ми можемо одержати її з нерівності (IV), замінивши в ній х на х₀. Це означає, що х₀ є розв’язком нерівності (IV), тобто х₀ÎТ₄. Оскільки значення х₀ÎТ₁ ми вибирали довільно, то наші міркування можна повторити відносно будь-якого елемента цієї множини. А це означає, що кожен елемент множини Т₁, тобто кожен розв’язок нерівності (І), є елементом множини Т₄, тобто є розв’язком нерівності (ІУ). Отже, на основі означення підмножини маємо: Т₁ÌТ₄. Першу частину теореми доведено.

У другій частині доведемо, що кожен розв’язок нерівності (IV) є розв’язком нерівності (І). Виберемо довільне y₀єТ₄ÌХ і підставимо його у нерівність (IV). Тоді одержимо істинну числову нерівність f(y₀)·j(y₀)<g(y₀)·j(y₀). Оскільки j(y₀) - це числовий вираз, що приймає від’ємних значень для всіх у₀ÎХ. Поділивши на нього обидві частини нерівності f(y₀)·j(y₀)<g(y₀)·j(y₀), ми одержимо істинну числову нерівність f(y₀)>g(y₀) (Чому?). Цю нерівність f(y₀)>g(y₀) можна одержати з нерівності (І), замінивши х на y₀. Отже, y₀ є розв’язком нерівності (І). Оскільки y₀єТ₄ ми вибирали довільно, то наші міркування можна повторити відносно будь-якого елементу y₀єТ₄. Це означає, що кожен елемент множини Т₄ є елементом множини Т₁, тобто Т₄ÌТ₁.

Таким чином, у першій частині ми довели, що Т₁ÌТ₄., а в другій – що Т₄ÌТ₁. На основі означення рівності множин це означає, що Т₁=Т₄. Отже, ми показали, що множини розв’язків нерівностей (І) і (ІV) співпадають. Оскільки вони задані на одній множині Х, то ці нерівності рівносильні. Теорему доведено повністю.

3. Розглядаючи рівняння та нерівності з однією та двома змінними, системи та сукупності рівнянь з двома змінними, ми давали відповідні означення. Аналогічно можна визначити поняття системи та сукупностей нерівностей, та інші поняття які пов’язані з ними.

Означення: системою двох нерівностей з однією змінною, заданих на одній і тій самій множині, називається кон’юнкція цих нерівностей.

Означення: сукупністю двох нерівностей з однією змінною, заданих на одній і тій самій множині, називається диз’юнкція цих нерівностей.

Символічно систему двох нерівностей з однією змінною в загальному вигляді позначають так: f₁(х)<g₁(х)Ùf₂(х)<g₂(х) або

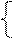f₁(х)<g₁(х)

f₂(х)<g₂(х). Відповідно сукупність двох нерівностей з однією змінною в загальному вигляді позначають так: f₁(х)<g₁(х)Úf₂(х)<g₂(х) або

f₁(х)<g₁(х)

f₂(х)<g₂(х).

Означення: розв’язати систему нерівностей - це означає знайти такі значення змінної із множини хєХ, які перетворюють кожну нерівність системи в істинну числову нерівність.

Означення: розв’язати сукупність нерівностей - це означає знайти такі значення змінних хєХ, які задовольняють хоча б одну нерівність сукупності.

Вище ми визначили поняття системи і сукупності нерівностей з однією і двома змінними, з’ясували, що означає розв’язати систему або сукупність нерівностей, а тепер перейдемо до розгляду способів їх розв’язання. Найбільш поширеними серед цих способів є наступні: а) графічний спосіб; б) аналітичний спосіб. Суть першого полягає в тому, що в одній й тій самій системі координат зображають множину розв’язків кожної нерівності системи чи сукупності. Потім для системи нерівностей шукають перетин множин розв’язків, тобто спільні розв’язки всіх нерівностей системи. Для знаходження множини розв’язків сукупності нерівностей шукають об’єднання множин розв’язків кожної нерівності сукупності, тобто ті розв’язки, які задовольняють хоча б одну нерівність сукупності. В математиці під графіком нерівності розуміють множину її розв’язків, зображених на координатній площині. У математиці доведені наступні твердження, які допомагають при графічному розв’язуванні систем і сукупностей нерівностей.

Твердження 1: множиною розв’язків нерівності х>а (х³а) є права півплощина, на які пряма х=а поділяє координатну площину (у випадку х³а разом з прямою х=а) (див. малюнок № 6.5.).

Малюнок № 6.5. Множина розв’язків нерівностей х>а і х³а .

Твердження 2: множиною розв’язків нерівності х<а (х≤а) називається ліва півплощина, на які пряма х=а розбиває координатну площину (у випадку х≤а разом з прямою у=а).

Твердження 3: множиною розв’язків нерівності у>а (у≥а) є верхня із півплощин, на які пряма у=а розбиває координатну площину (у випадку у³а разом з прямою у=а).

Твердження 4: множиною розв’язків нерівності у<а (у≤а) є нижня півплощина, на які пряма у=а розбиває координатну площину (у випадку у≤а разом з прямою у=а).

Твердження 5: множиною розв’язків нерівності y<kx+b є нижня із півплощин, на які ця пряма розбиває координатну площину, без прямої y=kx+b.

Твердження 6: множиною розв’язків нерівності y>kx+b є верхня із півплощин, на які ця пряма розбиває координатну площину, без прямої y=kx+b (див. малюнок № 6.6.).

Малюнок № 6.6. Множина розв’язків нерівностей y<kx+b і y>kx+b.

Твердження 7: множиною розв’язків нерівності y≤kx+b є нижня із півплощин, на які пряма у=kx+b розбиває координатну площину, разом з прямою у=kx+b.

Твердження 8: множиною розв’язків нерівності y³kx+b є верхня із півплощин, на які пряма у=kx+b розбиває координатну площину, разом з прямою у=kx+b.

Твердження 9: множиною розв’язків нерівності (х-а)²+(у-b)²<R² є та частина координатної площини, яка знаходиться всередині кола з центром в точці (а,b) і радіусом R без точок кола (х-а)²+(у-b)²=R².

Твердження 10: множиною розв’язків нерівності (х-а)²+(у-b)²>R² є та частина координатної площини, яка знаходиться поза колом з центром в точці (а,b) і радіусом R без точок кола (х-а)²+(у-b)²=R².

Твердження 11: множиною розв’язків нерівності (х-а)²+(у-b)²≤R² є та частина координатної площини, яка знаходиться всередині кола з центром в точці (а,b) і радіусом R з точками кола (х-а)²+(у-b)²=R².

Твердження 12: множиною розв’язків нерівності (х-а)²+(у-b)²≥R² є та частина координатної площини, яка знаходиться поза колом з центром в точці (а,b) і радіусом R з точками кола (х-а)²+(у-b)²=R² .

Із розв’язанням систем і сукупностей нерівностей, досить часто доводиться зустрічатися при розв’язанні дробово-раціональних нерівностей та нерівностей, одна частина яких є добутком, а інша дорівнює 0. Покажемо це на конкретному прикладі.

Вправа: розв’язати нерівність: 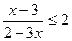, обґрунтовуючи виконувані дії теоремами про рівносильність нерівностей.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Доведення.	\|	Розв’язання.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.