Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Якщо маємо систему функцій

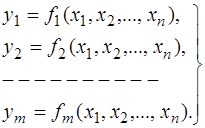. (7.98)

Вага системи функцій (7.98) для незалежних аргументів визначиться за формулою

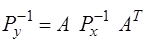, (7.99)

де ;

де 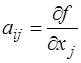; K_х – кореляційна матриця аргументів х_і; – дисперсія одиниці ваги; 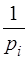– обернені ваги аргументів.

Після перемноження матриць у формулі (7.99) отримаємо

, (7.100)

де 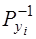– обернені ваги функцій у_і ;

K_ij – кореляційні моменти, які характеризують зв’язок між вагами функції.

Коефіцієнти кореляції між функціями визначаться за формулою

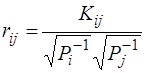. (7.101)

Приклад. Для системи нівелірних ходів з двома вузловими точками відома кореляційна матриця вектора відміток h = f(H)(рис.7.2).

Рис.7.2

Визначити кореляційну матрицю обернених ваг перевищень.

Розв’язання. Матриця обернених ваг висот вузлових точок при мм буде

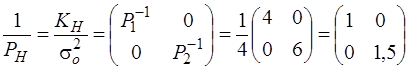Складемо функції перевищень і визначимо матрицю А.

h₁ = H₁ - H_B ,

h₂ = H₂ – H₁,

h₃ = H_C – H₂, ; .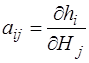

h₄ = H_B – H₁,

h₅ = H₂ – H_B.

Визначаємо матрицю обернених ваг за формулою 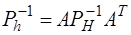, або

= ,

або

Тобто ; ; ; ; .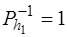

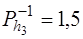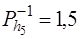За формулою (7.101) визначаємо нормовану кореляційну матрицю, або матрицю коефіцієнтів кореляції між перевищеннями мережі нівелірних ходів

Аналіз кореляційної матриці показує, що зв’язок існує між суміжними перевищеннями. Причому r_ij має знак плюс (+), коли ходи направлені в одну сторону і мінус (-), коли вони протилежних напрямків.

§ 5. Розрахунок точності вимірів

На стадії проектування висувають вимоги до точності виконання геодезичних вимірювань.

Практично результат вимірювання величини у є функцією від виміряних аргументів х₁, х₂, ..., х_п, тобто

у = f (х₁, х₂, ..., х_п ). (7.102)

При розрахунку точності вимірів аргументів х_і(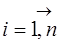)висувають вимогу, щоб похибка визначення функції не перевищувала деякого граничного значення W_гр.

Залежно від заданої ймовірності розраховують середню квадратичну похибку функції за формулою

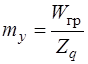, (7.103)

де Z_q – вибирається із таблиць розподілу Лапласа (дод. 6), залежно від рівня значимості q = 1 – p.

На стадії проектних розрахунків приймають, що аргументи функції у незалежні між собою. З врахуванням формули (7.82) для функцій (7.102) будемо мати

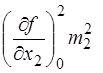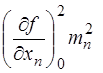+ + ... + . (7.104)

Залежно від умов проектування та виконання геодезичних робіт застосовують моделі розрахунку, описані нижче

1. Принцип рівного впливу

Він полягає в тому, що умовно приймають рівним вплив кожної із похибок аргументів (складових функції (7.104)), тобто

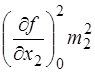= = ... = . (7.105)

Формула (7.104) зведеться до виду

. (7.105а)

Тоді 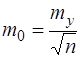. (7.106)

Середні квадратичні похибки вимірювання окремих аргументів визначаться за формулою

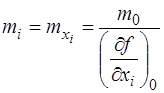, (7.107)

або 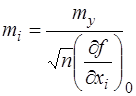, (7.108)

де п – кількість аргументів функції.

Приклад. Перевищення між точками через водну перешкоду на відстані S = 200м визначається способом тригонометричного нівелювання за формулою . Кут нахилу лінії складає n = +3^о. Визначити точність вимірювання лінії та кута, якщо допустима похибка нівелювання не повинна перевищити мм при заданій імовірності р = 0,99.

Розв’язання. Визначаємо середню квадратичну похибку функції за формулою (7.103). Із таблиць розподілу Лапласса (дод. 6) при q = 1 – p = = 1–0,99 = 0,01 визначаємо Z_q = 2,58.

Відповідно

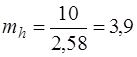мм.

Визначаємо за правилами § 4, розд.7 дисперсію перевищення

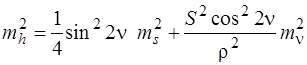За формулою (7.105) приймаємо

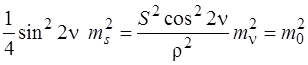тоді , відповідно мм.

Середня квадратична похибка вимірювання лінії буде дорівнювати

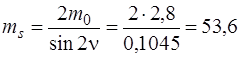мм =0,05 м.

Середня квадратична похибка вимірювання кута нахилу буде дорівнювати

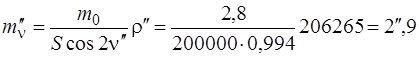Можна обчислити граничні похибки при р = 0,99.

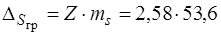= 138,3 мм

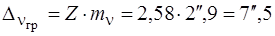Відповідно відносна гранична похибка лінійних вимірювань буде дорівнювати

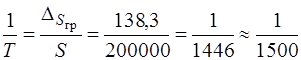Аналіз показує, що при визначенні перевищення через водну перешкоду необхідно буде використати світловіддалемір та точний теодоліт або електронний тахеометр.

2. Принцип введення коефіцієнтів співвідношення точності

На стадії проектування, шляхом аналізу існуючих технологій виконання робіт, наявності геодезичних приладів або визначення зовнішніх умов і т.д. може бути встановлено, що деякі аргументи функції (7.102) повинні (можуть) бути виміряні з більшою або меншою точністю. Тоді в формулі (7.104) можна встановити коефіцієнти K_і співвідношення точності впливу її окремих складових правої частини формули. В формулі (7.105) отримаємо

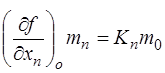; , ... , . (7.109)

Формула (7.104) зведеться до виду

. (7.110)

Тоді 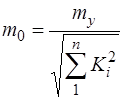. (7.111)

Середні квадратичні похибки вимірювання окремих аргументів визначаться за формулою

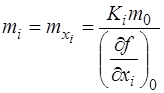. (7.112)

Практично, аналізуючи результати розрахунків з врахуванням можливих технологій виконання робіт, можна визначити найбільш економічно обґрунтовані коефіцієнти співвідношення точності геодезичних вимірювань – K_і.

Приклад. Аналіз похибок вимірювання відстаней і кутів в попередньому прикладі при визначені перевищення через недосяжну відстань тригонометричним нівелюванням показав:

1) відстані слід вимірювати віддалеміром з досить невисокою відносною похибкою ;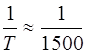

2) кут нахилу необхідно вимірювати з високою точністю, коли гранична похибка повинна не перевищувати .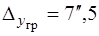

Розв’язання. Аналіз показує, що при застосуванні сучасних світловіддалемірів для вимірювання відстаней, їх точність буде значно вищою. В той же час вимірювання кута нахилу з високою точністю досить складно.

Тому доцільно підвищити точність вимірювання відстані, при цьому знизиться точність вимірювання кута нахилу.

Для початку встановимо таке співвідношення точності: K₁ = 1, K₂ =5.

За формулою (7.111) маємо при m_y = 3,9 мм

мм.

За формулою (7.108) обчислюємо середні квадратичні похибки вимірювання ліній та кута нахилу

мм;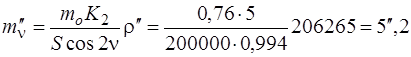

При р = 0,99 і Z_q = 2,58 обчислимо граничні похибки

мм

Відносна похибка лінійних вимірювань буде

Розрахунки показують, що при цьому можна використати топографічний світловіддалемір СТ-5 та теодоліт Т5, що є більш оптимальним.

§ 6. Сумісний вплив систематичних та випадкових похибок

При проведенні геодезичних вимірів постійно змінюється “комплекс умов”. Це призводить до виникнення похибок вимірів. За походженням похибки можуть бути випадковими і систематичними (§ 1, розд.6).

Тому істинну похибку визначають за формулою

D_і = х_і – Х, (7.113)

де х_і – виміряна величина;

Х – істинне значення виміряної величини.

Оскільки істинні похибки включають в себе як випадкові d_і,так і систематичні l_і похибки, то при п повторних вимірах отримаємо

D_і = d_і + l_і ; 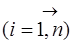. (7.114)

Зведемо їх до квадрата, складемо і поділимо на п

. (7.115)

В формулі (7.115) маємо ; ; .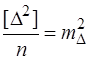

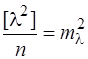Керуючись четвертою властивістю компенсації випадкових похибок отримаємо

.

Тоді формула (7.115) зведеться до виду

. (7.116)

Розглянемо функцію у = f( x₁, x₂, …, x_n).

Тоді D_у = d_у + l_у.

При цьому в разі лінійної функції будемо мати похибки d_у та l_у як функції

d_у = d₁ + d₂ + ... + d_п , (7.117)

l_у = l₁+ l₂+ ...+ l_п. (7.118)

За правилами визначимо дисперсію функції (7.117)

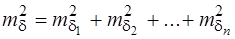. (7.119)

Беручи до уваги, що систематичні похибки односторонні і не мають властивості компенсації, то за формулою (7.118) отримаємо

. (7.120)

Припустимо, що , 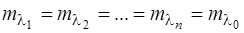. Тоді формула (7.116) з врахуванням формул (7.119), (7.120) набуде виразу

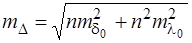, (7.121)

або . (7.122)

Аналіз формули (7.122) показує, що систематичні похибки в п - разів більше впливають на результат виміру, ніж випадкові похибки. Тому постає питання про розробку технології виконання геодезичних вимірів, яка до мінімуму зменшує вплив дії систематичних похибок.

Цього досягають шляхом:

а) дослідження законів виникнення систематичних похибок, визначенням їх величини і введенням поправок в результати вимірів, наприклад,при лінійних вимірюваннях на компараторах визначаються поправки компарування на одиницю виміру D_kі безпосередньо вводять їх в результати вимірів;

б) розробки методики вимірювальних робіт, яка ліквідує дію систематичної похибки, або зводить її до мінімуму, наприклад, вимірювання кутів при крузі “право” (КП) та крузі “ліво” (КЛ) зводить вплив колімаційної похибки практично до нуля. При нівелюванні І-ІІІ класів перевищення вимірюють в прямому та зворотному напрямках, декількома рейками по декількох костилях залежно від точності нівелювання;

в) в результаті математичної обробки вимірів визначають закон і величину дії систематичних похибок і вносять в результати зрівнених величин, наприклад, в результаті кореляційного аналізу визначають закон дії похибок і силу зв’язку між виміряними величинами. При зрівнюванні враховують отримані дані, що підвищує кінцеву точність зрівнених величин.

Запитання для самоперевірки

1. Як визначити, що виміри рівноточні?

2. Приведіть формулу середнього арифметичного.

3. Як обчислити систематичну похибку?

4. Як обчислити істинні та ймовірні похибки?

5. Приведіть формулу Гаусса і Бесселя.

6. За яких умов застосовують формулу Гауса, а за яких формулу Бесселя?

7. Які контролі виконуються при обробці рівноточних вимірів?

8. Як визначити середню квадратичну похибку середнього арифметичного?

9. Назвіть середні квадратичні похибки середніх квадратичних похибок.

10. Приведіть порядок обробки рівноточних вимірів.

11. Дайте визначення нерівноточних вимірів.

12. Як обчислити ваги вимірів і що вони визначають?

13. Приведіть формули обчислення середньої квадратичної похибки одиниці ваги.

14. Приведіть формулу загальної арифметичної середини.

15. Як виконати інтервальну оцінку?

16. Приведіть порядок обробки нерівноточних вимірів.

17. Наведіть приклади подвійних рівноточних і нерівноточних вимірів.

18. Як виконати оцінку точності подвійних рівноточних вимірів?

19. Як виконати оцінку точності подвійних нерівноточних вимірів?

20. Приведіть формулу дисперсії функції виміряних величин для залежних аргументів.

21. Приведіть формулу дисперсії функції виміряних величин для незалежних аргументів.

22. Приведіть формулу дисперсії системи функцій.

23. Напишіть формулу для обчислення ваги функції.

24. Сформулюйте правила обчислення дисперсії та ваги функції.

25. Як виконувати розрахунок точності аргументів функції?

26. Що таке принцип рівного впливу?

27. Що таке принцип коефіцієнтів співвідношення точності?

28. Як діють систематичні і випадкові похибки?

29. Як зменшують дію систематичних похибок?

Читайте також:
Автономну, незалежну від будь1якої іншої, систему фінансування.
Аденогіпофіз, його гормони, механізм впливу, прояви гіпер- та гіпофункцій.
Аутентифікація з використанням односторонніх функцій
Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
В десяткову систему числення
В случае отсутствия внешних сил (рассматриваем замкнутую систему)
Вага системи функцій
Важкість праці: Динамічні, статичні навантаження. Напруженість праці. Увага, напруженість аналізаторних функцій, емоційна та інтелектуальна напруженість, монотонність праці.
Введення даних у систему
Види договорів і контрактів. Розподіл функцій учасників проекту
Види функцій державного управління
Види функцій державного управління

Переглядів: 1088

<== попередня сторінка | наступна сторінка ==>

|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.014 сек.