Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Середня квадратична похибка окремого виміру

Теоретично мірою точності вимірів є дисперсія s². За результатами статистичної обробки рядів вимірів визначають емпіричну (або статистичну) дисперсію m²(§4, розд.4).

За ММП Фішера доведено, що коли статистичний ряд х₁, х₂, ..., х_п підкоряється нормальному закону розподілу, ефективною оцінкою точності є дисперсія

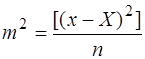. (6.23)

Оскільки розмірність дисперсії (“в квадраті”), то за міру точності приймають емпіричний стандарт або середню квадратичну похибку

, (6.24)

де D_і= х_і – Х– істинні похибки.

Її називають формулою Гаусса.

Якщо невідоме істинне значення вимірюваної величини, то за формулою (6.6) використаємо різниці

, (6.25)

де l–систематична похибка.

Коли число вимірів дорівнює n, із формули (6.25) отримаємо

D_і= V_i + l, . (6.26)

Зведемо вираз (6.26) до квадрату і підсумуємо

[D²] = [V²] + nl²+ 2l[V].(6.27)

Якщо в формулі (6.4) взяти суму ймовірних похибок V, то отримаємо

. (6.28)

Оскільки середнє арифметичне за формулою (6.21) дорівнює , то в формулі (6.28) отримаємо

або [V] = 0.

Формула (6.28) використовується і для контролю обчислення ймовірних похибок V.

Тоді формула (6.27) зведеться до вигляду

[D²] = [V²] + nl². (6.29)

Якщо вираз (6.29) поділити на n, то з врахуванням формули (6.23) отримаємо

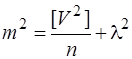. (6.30)

Істинна похибка lпростої арифметичної середини за формулами (6.6) і (6.20) буде

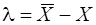або . (6.31)

Тоді в формулі (6.30) l² з врахуванням формули (6.31) буде

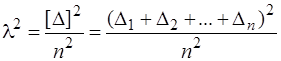або 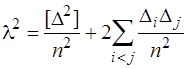. (6.32)

Згідно з четвертою властивістю випадкових похибок

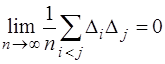а формула (6.32) зведеться до вигляду

. (6.33)

З врахуванням формули (6.30) та (6.33) отримаємо

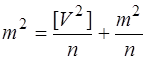Остаточно отримаємо формулу Бесселядля визначення середньої квадратичної похибки виміру за ймовірними похибками

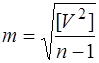. (6.34)

3. Середня квадратична похибка арифметичної середини

Скористаємося формулою (6.21) і запишемо

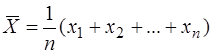. (6.35)

Оскільки виміри рівноточні, тобто , а часткові похідні , то за формулою (3.59) отримаємо дисперсію середнього арифметичного

. (6.36)

Тоді середня квадратична похибка арифметичного середнього буде

. (6.37)

Додатково обчислюють:

4. Середню квадратичну похибку середньої квадратичної похибки

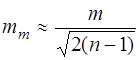. (6.38)

5. Середню квадратичну похибку середньої квадратичної похибки арифметичного середнього

. (6.39)

Для оцінки точності похибок вимірів використовують інші критерії.

6. Середню похибку q, як середнє арифметичне із суми абсолютних значень випадкових похибок, тобто

, (6.40)

де [|D|] = |D₁| + |D₂| + … + |D_n|.

7. Серединну похибку r.Її визначають в середині зростаючого ряду

|D_min|, |D₁|, |D₂|, …, |D_max|,

складеного із абсолютних значень похибок вимірів. Тоді ймовірність серединної похибки буде

p(|D| £r) = . (6.41)

Середня квадратична похибка виміру m має зв’язок з середньою qта серединною rпохибками

m »1,25 q;(6.42)

m »1,48 r. (6.43)

8. Абсолютні похибки. До них належать: середня квадратична (m),середня квадратична арифметичного середнього (М),середня (q), серединна (r), істинна ( D_і),ймовірна (V_i)і гранична (D_гр.).

9. Відносні похибки. Відношення абсолютної похибки до значення виміряної величини називають відносною похибкою.

Назва відносної похибки відповідає назві абсолютної похибки, наприклад:

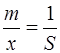– середня квадратична відносна похибка;

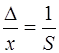–істинна відносна похибка;

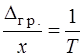- гранична відносна похибка тощо.

Оцінка точності вимірів за допомогою середніх квадратичних похибок mпорівняно з середньою та серединною похибками має такі переваги:

1. Обґрунтованості: ймовірність 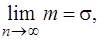тобто при умовах коли число вимірів прямує до нескінченності, середня квадратична похибка прямує до абсолютного значення стандарту.

2. Ефективності:m²= min, тобто значення дисперсії буде мінімальним.

3. На величину середньої квадратичної похибки mвплив більшихза абсолютним значенням похибок|D_max| найбільший.

4. Середня квадратична похибка mзв’язана з граничною похибкою відношенням

|D_гр| £t ×m,

де t–вибирається із таблиць розподілу Лапласа або Стьюдента залежно від надійної ймовірності рта кількості вимірів n.

5. Середня квадратична похибка визначається достатньо надійно при обмеженій кількості вимірів.

§ 4. Числові характеристики нерівноточних вимірів

В практиці геодезичних вимірювань може відчутно порушуватися “комплекс умов”: виміри виконують приладами різної точності або різними методами, значно змінюються зовнішні умови (температура, вологість тощо) чи інші чинники. Тоді дисперсії таких вимірів значно відрізняються між собою 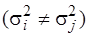і їх називають нерівноточними.

Нерівноточні виміри можна виразити статистичним рядом

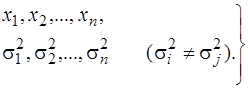. (6.44)

Задача виникає, коли за результатами нерівноточних вимірів однієї і тієї величини необхідно визначити найбільш надійне значення виміряної величини і виконати оцінку точності вимірів за допомогою числових характеристик.

В теорії похибок вимірів до числових характеристик нерівноточних вимірів відноситься:

1. Вага вимірів.Розглянемо статистичний ряд нерівноточних вимірів (6.44), який будемо характеризувати емпіричними дисперсіями

. (6.45)

Введемо величини 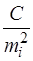, обернено пропорційні квадратам середніх квадратичних похибок (емпіричних дисперсій ) і позначимо

, (6.46)

де С– постійний умовно прийнятий коефіцієнт такої величини, щоб значення ваги р_ібуло ближче до одиниці.

Величину р_іназивають вагами нерівноточних вимірів. Тоді нерівноточні виміри можна характеризувати статистичним рядом

(6.47)

Якщо дисперсія є мірою абсолютної точності результату, то вага є мірою відносної точності.

Вага вказує наскільки точність одного виміру більш або менш точна відносно іншого в ряду вимірів.

Наприклад. Маємо статистичний ряд

Хх₁, х₂, х₃, х₄

Р1,8; 1,0; 0,5; 2,0.

За значеннями ваг р_і можна зробити висновок, що перший результат наближено в 1,8 рази точніше другого, в 3,6 рази ( 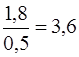) точніше третього, але в 1,11 ( 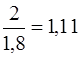) менш точно від четвертого; результат другого виміру в два рази точніше третього, але в 2 рази менш точно від четвертого виміру і т.д.

Практично в більшості випадків невідома дисперсія або середня квадратична похибка вимірів m_i.Ваги вимірів обчислюють за наближеними формулами

; (6.48)

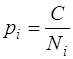; (6.49)

, (6.50)

де L_i– довжина лінії, ходу або полігона;

N_i– кількість виміряних величин (кутів, перевищень, станцій і т.д.);

n_i– кількість вимірів однієї і тієї величини (число прийомів).

Аналогічно коефіцієнт Свибирають так, щоб ваги р_і за величиною були близькі до одиниці для зручності обчислень.

В практичних розрахунках часто використовують приведені ваги

, (6.51)

де [p] = p₁ + p₂ +…+p_n,тоді [p´] = 1.

Ряд нерівноточних вимірів можна звести до рівноточного, якщо кожен вимір помножити на величину 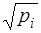. Статистичний ряд

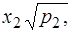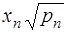..., (6.52)

буде рівноточним.

2. Загальне середнє арифметичне

Припустимо, що в результаті вимірів однієї величини отримано статистичний ряд нерівноточних результатів

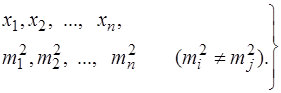. (6.53)

Найкращі оцінки отримують тоді, коли виміри х_іабо їх похибки D_і, підкоряються нормальному закону розподілу.

Перейдемо до нормованих похибок

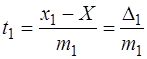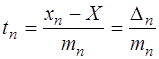; , ..., , (6.54)

де Х– істинне значення вимірюваної величини.

Функція щільності нормованого нормального закону розподілу визначається за формулою

.

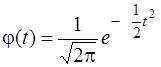Числові характеристики визначаються за результатами всіх вимірів. Тоді функція щільності сумісного розподілу ряду випадкових величин t₁,t₂, …, t_kбуде

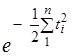. (6.55)

Найбільш надійне значення шуканого параметра t для нерівноточних вимірів буде відповідати максимальному значенню функції j(t₁, t₂, …, t_n).Із формули (6.55) видно, що це відбудеться за умови, коли показник степеня буде мінімальним, тобто

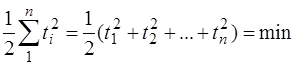. (6.56)

З врахуванням формули (6.54) отримаємо

. (6.57)

Для визначення екстремуму функції (6.57) візьмемо першу похідну за перемінними х_і_,прирівняємо до нуля і отримаємо

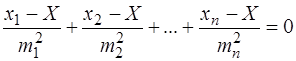, (6.58)

Умовно помножимо їх на довільне число С, отримаємо

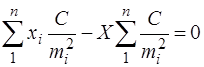. (6.59)

Оскільки 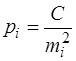, то отримаємо

[xp] –X[p] = 0. (6.60)

Ймовірно .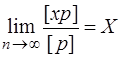

Це означає, що частка при необмеженій кількості вимірів прямує до істинного значення. Його називають загальним середнім арифметичним

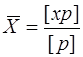, (6.61)

або . (6.62)

В разі рівноточних вимірів р₁= р₂ = ... = р_п = 1,а[p] = n.

Тоді формула (6.61) зводиться до простої арифметичної середини

,

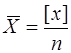тому формулу (6.61) і називають загальною середньою арифметичною.

3. Середня квадратична похибка одиниці ваги

Нерівноточні виміри характеризують дисперсіями або мірою відносної точності р_і. Умовно із ряду нерівноточних вимірів виберемо результат такого виміру х_k, вага якого буде дорівнювати одиниці, тобто р_k= 1. Дисперсію цього результату позначимо через m². Тоді

, (6.63)

абосередня квадратична похибка одиниці ваги буде дорівнювати: m= m_k. Оскільки , то m= m_k, або

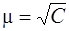; (6.64)

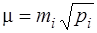. (6.65)

Тоді середня квадратична похибка будь-якого виміру визначиться за формулою

. (6.66)

При р= 1 m_i= m –тобто середня квадратична похибка одиниці ваги є мірою точності того результату виміру, вага якого дорівнює одиниці.

Визначимо середню квадратичну похибку одиниці ваги:

а) при заданому істинному значенні виміряної величини

В результаті нерівноточних вимірювань однієї і тієї ж величини Хотримано статистичний ряд

, (6.67)

де –істинні похибки нерівноточних вимірів,

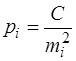–вага вимірів.

Згідно з формулою (6.52) зведемо ряд нерівноточних похибок вимірів до рівноточного ряду

, . (6.68)

Оскільки ряд (6.68) є рівноточним і підкоряється нормальному закону розподілу, то за формулою Гаусса (6.24) можна визначити середню квадратичну похибку m вимірів. Для виміру вага якого дорівнює одиниці р = 1. Це буде середня квадратична похибка одиниці вагиm, або

,

або 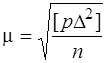. (6.69)

б) при обчисленому загальному середньому арифметичному

Як і в рівноточних вимірюваннях використаємо формулу (6.25), тобто

р_і,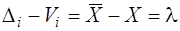; . (6.70)

де –загальне середнє арифметичне;

Х–істинне значення вимірюваної величини.

Зробимо перетворення

.

Тобто, при нерівноточних вимірах і наявності істинних похибок систематична похибка lвизначиться за формулою

. (6.71)

Для спрощення доказів складемо ряд ймовірних похибок

р_і , . (6.72)

Оскільки , то

[pV] = 0 .(6.73)

З формули (6.72) ряд імовірних похибок теж є нерівноточним. Як і в попередньому випадку зведемо їх до рівноточного вигляду

, . (6.74)

Оскільки ряд (6.74) є рівноточним і за умовами підкоряється нормальному закону розподілу, то за формулою Бесселя (6.34) визначимо середню квадратичну похибку m.Для виміру, вага якого буде дорівнювати одиниці (р = 1),згідно з формулою (6.65) вона буде дорівнювати середній квадратичній похибці одиниці ваги, тобто m

,

або 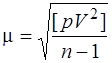. (6.75)

4. Середня квадратична похибка загального середнього арифметичного

Формулу загального середньоарифметичного (6.62) отримаємо у вигляді

. (6.76)

За формулою (3.59) дисперсія функції F(x) при 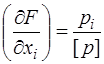отримаємо

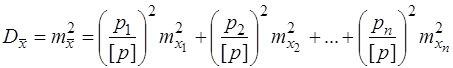(6.77)

Оскільки за формулою (6.66) 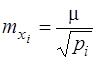то формула (6.77) зведеться до вигляду

,

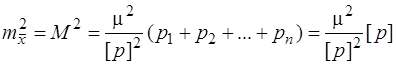або 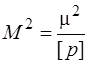. (6.78)

Згідно з формулою (6.78) середня квадратична похибка загального середнього арифметичного при нерівноточних вимірах визначиться за формулою

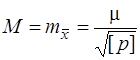. (6.79)

Додатково обчислюють:

5. Середню квадратичну похибку середньої квадратичної похибки одиниці ваги

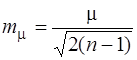. (6.80)

6. Середню квадратичну похибку середньої квадратичної похибки загального середнього арифметичного

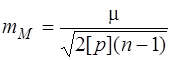. (6.81)

7. При необхідності визначають середні квадратичні похибки окремих вимірів

. (6.82)

Відносні похибкиобчислюють так само як і при рівноточних вимірах (§ 3; розд.6).

Запитання для самоперевірки

1. Які задачі вирішує теорія похибок вимірів?

2. Які складові комплексу умов?

3. Назвіть види вимірювань.

4. Яка роль надлишкових вимірів?

5. Назвіть види похибок вимірів.

6. Яка природа виникнення випадкових похибок?

7. Які виміри є рівноточними?

8. Які виміри є нерівноточними?

9. Що характеризує проста арифметична середина?

10. Що характеризує середня квадратична похибка m?

11. Що характеризує середня квадратична похибка М?

12. Які числові характеристики рівноточних вимірів Ви знаєте?

13. Що таке вага виміру і як її визначити?

14. Що характеризує загальне середнє арифметичне?

15. Що характеризує середня квадратична похибка одиниці ваги?

16. Як визначити середню квадратичну похибку нерівноточного виміру?

17. Що визначає середня квадратична похибка Мпри нерівноточних вимірах?

18. Як визначити відносні похибки?

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Тоді із різниці формул (6.3) та (6.4) отримаємо	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.015 сек.