• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рівняння молекулярно-кінетичної теорії ідеального газу для тиску

У молекулярно-кінетичній теорії користуються моделлю ідеального газу, що задовольняє такі умови:

1) власний об'єм молекул газу нехтовно малий порівняно з об'ємом посудини;

2) між молекулами газу відсутні силпи взаємодії;

3) зіткнення молекул газу між собою і зі стінками посудини абсолютно пружні.

Модель ідеального газу можна ви­користати, вивчаючи реальні гази, оскільки вони при умовах, близьких до нормальних, а також при низьких тисках і високих температурах близькі за своїми властивостями до ідеального газу.

Основне рівняння молекулярно-кінетичної теорії пов'язує параметри газу з характеристиками руху його молекул, тобто встановлює залежність між тиском і об'ємом газу та кінетичною енергією поступального руху його молекул.

Тиск газу в посудині є результатом, зіткнення молекул газу із стінками посудини. Тиск газу є макроскопічним проявом руху молекул.

Розглянемо однорідний газ, який поміщений в посудину кубічної форми. Напрямимо осі системи відліку вздовж ребер куба (рис. 38). Нехай певна молекула М рухається в посудині зі швидкістю v. Швидкість v можна розкласти на три складові координатних осей:

v =v_x + v_y + v_z.

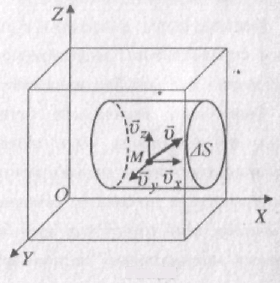Виділимо на стінці посудини елемен­тарну площину DS, яка перпендикулярна до осі X. При кожному зіткненні молекула передає площині імпульс 2m₀v_x , де m₀ – маса молекули. За час Dt площини досягнуть ті молекули, які знаходяться в об’ємі циліндра з основою DS і висотою v_xDt. Кількість цих молекул дорівнює nDSv_xDt, де n - кількість молекул в одиниці об’єму газу. З них тільки половина потрапляє на площину DS. Решта через повну безладність молекулярних рухів рухаеться не до стінки, а від неї. За час Dt об площину DS ударяються N_x = 1/2nDSDtv_x молекул газу.

Загальний імпульс, який переданий молекулами площини DP_x = =2m₀v_1xN_2x + 2m₀v_2xN_2x + … +2m₀v_lxN_lx = m₀DSDt(n₁v²_1x + n₂v²_2x + … +n_l2_lx), n₁,n₂…n_n – кількість молекул, що мають швидкості v₁,v₂…v_n, відповідно. Тиск газу на площину DS

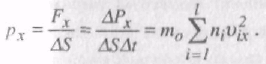Зважаючи на цілковиту хаотичність рухів молекул, тиск газу в будь-якому нанрямку повинен бути однаковий, тобто

p_x = p_y = p_z = p.

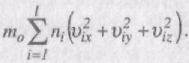Додамо почленно рівняння для p_x, p_y i p_z:

p_x + p_y+ p_z = 3p =

Через те, що v²_ix + v²_iy + v²_iz = v²_i , то

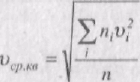Величина - це сума квадратів швидкостей усіх молекул в одиниці об'єму газу. При великій кількості молекул немає потреби знати значення квадрита швидкості кожної молекули. Тому знайдемо середнє значення цієї величини. За визначенням

Величина

називається середньою квадратичною швидкістю.

В результаті тиск газу дорівнюватиме:

Це рівняння називається основним рівнянням молекулярно-кінетичної теорії ідеального газу для тиску.

Знайдену формулу перепишемо у вигляді:

де <e_к> - середня кінетична енергія поступального руху однієї молекули газу.

Густина газу

Тоді

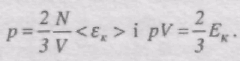Оскільки кінетична енергія поступаль­ного руху молекул газу Е_k = =N<e_к>, то

Це рівняння перепишемо так чином:

де m = Nm₀ - маса газу.

Для одного моля газу m = m і V = V_m.

Тоді pV_m = 1/3mv²_ср.кв.

З іншого боку, за рівнянням Менделєєва-Клапейрона

pV_m = RT

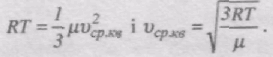Отже,

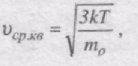
Оскільки m =m_oN_A, R = kN_A , де k - стала Больцмана, то

З рівняння Менделєєва-Клапейрона

101. Середня кінетична енергія

молекул. Молекулярно-кінетичне

трактування абсолютної температури

Знайдемо вираз для середньої кіне­тичної енергії поступального руху молеку­ли ідеального газу:

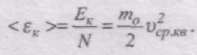
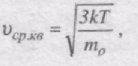Оскільки

То

Отже, середня кінетична енергія посту­пального руху молекул ідеального газу зале­жить тільки від його абсолютної тем­ператури, <e_к> прямо пропорційна до Т.

На рис. 39 зоб­ражено залежність <e_к> від Т. Якщо T = 0, <e_к> = 0, тоб­то припиняється поступальний рух молекул газу, а отже, дорівнює нулю і його тиск.

Отже, абсолютна температура є мі­ра середньої кінетичної енергії поступаль­ного руху молекул.

Однак в області температур, близь­ких до абсолютного нуля, поведінка молекул описується не класичними законами, а за­конами квантової механіки.

102. Розподіл Максвелла молекул

ідеального газу за швидкостями

теплового руху

Внаслідок безперервного хаотичного руху молекул, а також взаємного зіткнення молекул піл час цього руху кожна молекула зокрема може змінювати свою швидкість як за величиною, так і за напрямком. Тому в газі будуть як швидкі, так і повільні молекули. Але, хоча швидкості окремих молекул зміню­ються, властивості газу у стані термодинаміч­ної рівноваги загалом при цьому не змінюють­ся: залишаються постійними параметри систе­ми. Зумовлено це тим, що швидкості газових молекул підлягають певному законові, тобто, незважаючи на повну хаотичність молекуляр­них рухів, розподіл молекул за швидкостями виявляється не випадковим, а цілком визна­ченим. До того ж він є однозначним і єдино можливим.

Дж. Максвелл теоретично розв'язав задачу про розподіл молекул ідеального газу за швидкостями поступального руху. Він встановив закон, шо дає змогу визначити, яка кількість молекул dn із загальної кількості n молекул ідеального газу в одиниці об'єму мають при даній температурі швидкості, які лежать в інтервалі від v до v + dv. Дж. Максвелл вважав, що газ складається з великої кількості n однакових молекул, тем­пература в усіх частинах посудини з газом теж однакова і відсутні зовнішні дії на газ.

Якщо розбити діапазон швидкостей молекул на малі інтервали, які дорівнюють dv, то на кожний інтервал швидкості при­падатиме деяка кількість молекул dn(v), що мають швидкість в інтервалі dv.

Закон Максвелла описусться деякою функцією f(v), шо називається

функцією розподілу молекул за швидкостями руху.

Ця функція визначає відносну кількість молекул швидкості яких лежать в інтервалі від v до v + dv, тобто

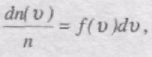
звідси

Застосовуючи методи теорії імовір­ності, Максвелл знайшов функцію f(v) у такому вигляді:

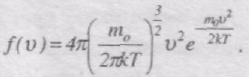
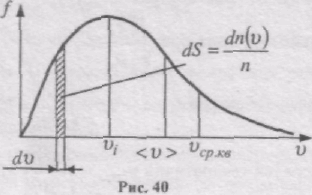Конкретний вигляд функції зале­жить від роду газу (m₀) і від параметра стану (Т). Графік функції f(v) наведений на рис. 40. Функція f(v) починається від нуля, досягає максимуму, а потім асимптотично пряму до нуля. Крива несиметрична відносно максимального значення f(v). Відносна кількість молекул dn(v)/n, швидкості яких лежать в інтервалі від v до v + dv, числово дорівнює площі заштрихованої ді­лянки на рис. 40.

Вся площа, обмежена кривою роз­поділу і віссю абсцис, числово дорівнює кількості молекул, швидкості яких мають різні значення від 0 до µ. Оскільки цю умову задовольняють всі n молекул, то площа, що розглядається, дорівнює одиниці:

Швидкість, при якій f(v) максимальна, називається найімовірнішою швидкістю v_i.

Використовуючи умову максимуму виразу f(v), можна знайти вираз для най­імовірнішої швидкості:

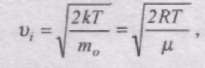
оскільки

Середня арифметична швидкість мо­лекул <v> визначається за формулою

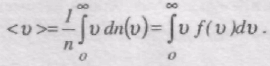
Підставляючи сюди f(v) й інтегру­ючи, отримаємо

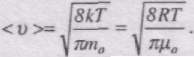
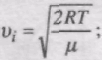Отже, є три швидкості, які характе­ризують стан газу (рис. 40):

найімовірніша

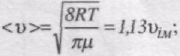
середня арифметична

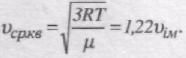
середня квадратична

При збільшенні температури (або зменшенні маси молекул) максимум кривої f(v) зміщується у бік більших швидкостей, а його абсолютна величина зменшується, причому площа, яка охоплена кривою f(v) і віссю v, залишається незмінною.

Закон Максвелла зручно формулювати, ввівши відносну швидкість

де v - дана швидкість, а v_i - найімовірніша швидкість для

молекул даного газу при даній температурі.

Розподіл, який визначає кількість мо­лекул, відносні швидкості яких лежать у межах від u_в до u_в + du_в , має такий вигляд:

Знайдемо середню відносну швид­кість молекул ідеального газу:

де <v> - середня арифметична швидкість.

103. Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі

Якщо на молекули не діють зовнішні сили, то вони рівномірно розподіляються по об'єму посудини. Однак молекули будь-якого газу завжди перебувають в полі сил тяжіння Землі. Якби не було тяжіння, то атмосферне повітря розсіялося б по всьому Всесвіту. Якби не було теплового руху молекул атмосфер­ного повітря, то всі вони впали б на Землю.

Тяжіння і тепловий рух приводять до стаціонарного стану газу, при якому його тиск і концентрація зменшується з висотою.

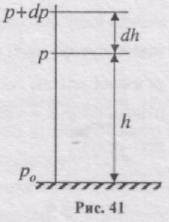Розглянемо ідеальний газ, маса всіх мекул якого однакова, температура постійна і який знаходиться в однорідному полі тяжіння. Якщо тиск газу на висоті h дорівнює p (рис.41), то на висоті h + dh він дорівнює p + dp, причому при dh > 0 dp <0, оскільки тиск з висотою зменшується.

Різниця тиску р і р+dp числово дорівнює вазі газу, що знаходиться в об'ємі циліндра заввишки dh, а площа основи, що дорівнює одиниці: p - (p + dp) = rgdh, де r - густина газу на висоті h.

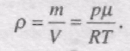Використаємо рівняння Менделєєва-Клапейрона

Звідси густина газу

Тоді

Вважаючи Т = соnst й ітегруючи по тиску від р₀ до р, а по висоті від 0 до h, отримуємо

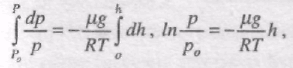
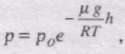звідси

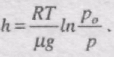
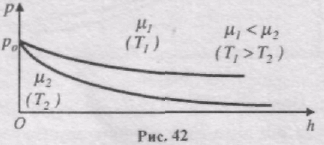Ці формули називаються барометричними формулами. Із них можна зро­бити висновок, що тиск газу зменшується із висотою експоненціально і тим швидше, чим важчий газ (чим більше m) і чим нижча температура (рис. 42).

Барометрична формула дає змогу знай­ти співвідношення між концентраціями газу на різній висоті. Використаємо рівняння стану ідеального газу у вигляді р = = nkt, де n - концeнтрація молекул газу. При Т = соnst отримуємо

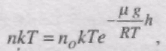
де n₀ - концепція молекул на висоті h = 0.

Оскільки m = m₀N_A, a R = kN_A, то

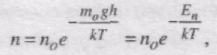
де Е_n - потенціальна енергія молекул в полі тяжіння. Отриманий вираз називається роз­поділом Больцмана у зовнішньому по­тенціальному полі.

Із збільшенням висоти концентрація молекул газу зменшується за експоненціальним законом (рис. 43). При високих темпе­ратурах кількість молекул n незначно зменшу­ється з висотою і при Т µ n n_{0 ,} тобто підвищення температури викликає вирівню­вання концентрації газу за висотою.

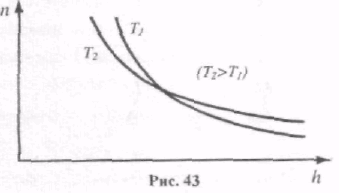
При Т 0К n 0, тобто всі мо­лекули під дією сили тяжіння опускаються на дно посудини.

104. Закон рівномірного розподілу енергії за ступенями вільності молекул

Числом ступенів вільності називають найменше число координат, які необхідно задати для того, щоб повністю визначи­ти положення тіла у просторі, або кіль­кість незалежних рухів, які може викону­вати тіло.

Матеріальна точка, шо довільно ру­хається у просторі, має три ступені вільнос­ті (x,у,z). Якщо ця точка рухається по деякій поверхні або вздовж певної кривої, то вона відповідно має два або один ступені вільності.

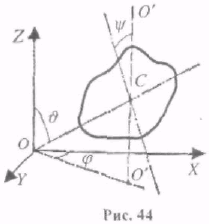Абсолютно тверде тіло має 6 ступенів вільності. Щоб визначити його положення в просторі, треба задати три координати (х,y,z) (3 ступені вільності поступального руху) центра мас тіла (рис. 44); два кути J і j визначають положення в просторі певної осі (О'О'), яка проходить через центр мас і якунебудь іншу фіксовану точку тіла і необхідно задати кут y, який визначає напрямок другої, зв'язаної з тілом осі, яка перпендикулярна до першої (J,j,y - 3 ступені вільності обертального руху).

Якшо тіло не абсолютно тверде і його частини можуть змінюватись одна відносно одної, то необхідно внести ще додаткові ступені вільності коливального руху.

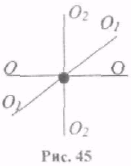Молекули одноатомного газу можна розглядати як матеріальні точки на тій під­ставі, що маса такої частинки зосереджена в ядрі, розміри якого дуже малі. Молекула одноатомного газу має три ступені вільності посту­пального руху (рис. 45).

Внаслідок хаотичності теплового руху молекул ідеальною газу в середньому на кожний ступінь вільності поступального руху одно­атомної молекули припадає однакова кінетична енергія <e_к1>, що дорівнює одній третині середньої кінетичної енергії молекули

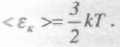
Отже,

Молекули, що складаються з двох, трьох і більшої кількості атомів, не можуть бути уподібнені до матеріальних точок.

Молекула двоатомного газу в першому наближенні - це два жорстко зв'язані атоми, що перебувають на деякій відстані один від одного. Положення такої системи можна ви­значити, якщо задати три координати центра мас системи і два куги J і j, які визначають напрямок у просторі осі системи.

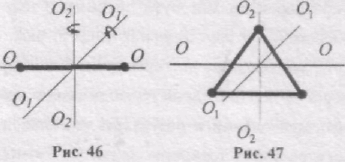Отже три ступені вільності будуть поступальними, а дві - обертальними нав­коло осей О₁-О₁, і О₂-О₂ (рис. 46). Обертання навколо третьої осі О-О розглядати не треба, бо момент інерції атомів відносно цієї осі дуже малий.

Триатомна і багатоатомні нелінійні мо­лекули (рис. 47) мають 6 ступенів вільності - 3 поступальні і 3 обертальні. Жорсткого зв'яз­ку між атомами не існує. Тому для реальних молекул необхідно враховувати також ступені вільності коливного руху.

У класичній статистичній фізиці виво­диться закон Больцмана про рівномірний розподіл енергій за ступенями вільності молекул: для статичної системи, що перебуває у стані термодинамічної рівноваги, на кожний поступальний і обертальний ступінь вільності припадає б середньому кінетична енергія, що дорівнює kT/2, а на кожний коливний ступінь вільності - в середньому енергія kT.

Коливний ступінь мас вдвоє більшу енергію тому, що на нього припадає не ли­ше кінетична енергія (як у разі поступаль­ного і обертального руху), але і потенціаль­на енергія, причому середні значення кі­нетичної і потенціальної енергій однакові:

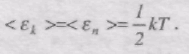
Таким чином, середня енергія молекули

де і = і_пост + і_об +2і_кол.

Важливою характеристикою термоди­намічної системи є її внутрішня енергія U - енергія хаотичного (теплового) руху мікрочастинок системи (молекул, атомів, електро­нів, ядер і тощо) і енергія взаємодії цих частинок. До внутрішньої енергії не належать кінетична енергія системи як цілого і потен­ціальна енергія системи у зовнішніх полях.

Внутрішня енергія - однозначна функ­ція термодинамічного стану системи, тобто в кожному стані система має цілком визначене значення внутрішньої енергії. Стан системи, в якому U = 0, цілком довільний, оскільки в термодинаміці інтерес становить не сама внутрішня енергія U системи, а її зміна DU при зміні стану системи.

В ідеальному газі немає сил вза­ємодії між молекулами, а отже, дорівнює нулю взаємна потенціальна енергія моле­кул. Тому для моля ідеального газу внут­рішня енергія дорівнює сумі кінетичних енергій N_A молекул:

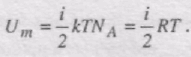
Якщо є n = m/m молів газу, то його внутрішня енергія

Внутрішня енергія ідеального газу залежить від кількості ступенів вільності молекул і абсолютної температури газу.

Лекція №40

105. Перший закон термодинаміки. Робота газу при зміні його об'єму

Розглянемо термодинамічну систему, для якої механічна енергія не змінюється, а змінюється лише її внутрішня енергія. Мож­ливі дві форми передавання енергії від одного тіла до іншого, а отже, і зміни внутрішньої енергії системи.

Перша з них зводиться до того, що енергія впорядкованого руху одного тіла переходить в енергію впорядкованого руху іншого тіла або його частин. Це може відбуватись під час взаємодії макроскопічних тіл, розміри яких у багато разів більші за розміри окремих атомів або молекул. Таку форму передавання енергії називають роботою. Наприклад, газ, що розширю­ється в циліндрі двигуна внутрішнього зго-ряння, переміщуе при цьому поршень і передає йому енергію у формі роботи.

Друга форма передавання енергії здій­снюється при безпосередньому обміні енер­гією між частинками взаємодіючих тіл, що рухаються хаотично. За рахунок переданої тілу енергії підсилюється невпорядкований рух його частинок, тобто збільшується внут­рішня енергія тіла. Таку форму передавання енергії в термодинаміці називають тепло­тою. Так, наприклад, при дотику холодного тіла і гарячого молекули другого тіла, які швидко рухаються, стикаються з молекулами першого тіла, що рухається повільніше, і передають їм частину своєї кінетичної енергії. Внаслідок цього внутрішня енергія першо­го тіла збільшується, другого - зменшується, а їх температури вирівнюються.

Отже, можна говорити про дві форми передачі енергії від одних тіл до інших: у формі роботи і у формі теплоти. Енергія механічного руху може перетворюватись в енергію теплового руху і навпаки. При цих перетвореннях має бути дотримано закону збереження і перетворення енергії, чим, по суті, застосовним до термодинамічних про­цесів і є перший закон термодинаміки, який сформульований в результаті узагальнення багатовікових дослідних даних.

Допустимо, що деяка система (газ, що знаходиться в циліндрі під поршнем), маючи внутрішню енергію U₁, отримала деяку кількість теплоти Q₁ і, перейшовши в новий стан, що характеризує внутрішню енергію U₂, виконала роботу А проти зовнішніх сил. Кількість теплоти вважа­ється додатною, коли вона підводиться до системи, а робота - позитивною, коли система виконує її проти зовнішніх сил.

Дослід показує, шо відповідно до зако­ну збереження енергії при довільному способі переходу системи з першого стану у другий зміна внутрішньої енергії DU = U₂ - U₁ до­рівнюватиме різниці між кількістю теплоти Q, отриманою системою, і роботою А, яка виконана системою проти зовнішніх сил:

DU = Q - A, або Q = DU + A.

Це рівняння є математичним вира­зом першого закону термодинаміки:

теплота, надана системі, витрачається на збільшення її внутрішньої енер­гії і на виконання системою роботи проти зовнішніх сил.

Вираз для першого закону термоди­наміки для малої зміни стану системи матиме вигляд: dQ = dU + dA або в коректнішій формі dQ = dU+ +dA, де dU - нескінченно мала зміна внутрішньої енергії системи, dА -нескінченно мала робота, dQ - нескінченно мала кількість теплоти. У цьому виразі dU є головним диференціалом, а dА і dQ такими не є.

Дуже важливим є випадок, коли сис­тема - це періодично діюча машина, в якій газ, пара або інше "робоче тіло" внаслідок деякого процесу повертається до початкового стану. У цьому разі DU = 0 і А = Q.

Робота, шо виконується машиною за один цикл, дорівнює підведеній ззовні теп­лоті Q. Цей висновок дає змогу сформулю­вати перший закон термодинаміки так: неможливо побудувати періодично діючий двигун, який виконував би роботу без підведення енергії ззовні або виконував би роботу більшу, ніж кількість переданої йому ззовні енергії (вічний овигун першого роду неможливий).

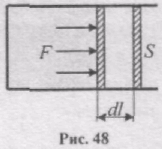
Знайдемо роботу, яка виконується газом при зміні його об'єму. Нехай газ знаходиться в цилінд­ричній посудині з пор­шнем (рис. 48).

Якщо газ, розширюючись, переміщує поршень на нескінченно малу відстань dl, то він виконує над ним роботу

dA = Fdl = pSdl = pdV,

де S - площа поршня, Sdl = dV - зміна об'єму газу.

Повну роботу А, яка виконана га­зом при зміні його об'єму від V₁ до V₂, знайдемо інтегруванням:

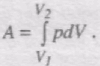
Результат інтегрування визначаєть­ся характером залежності між тиском і об'ємом газу.

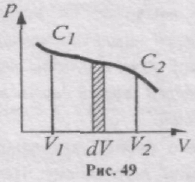Зобразимо графічно залежність тис­ку від об'єму (рис. 49). При збільшенні об'єму на dV виконана газом робота дорів­нює pdV, тобто вона числово дорівнює площі, яка заштрихована на рис. 49. Повна робота, що виконується газом при розши­ренні від об'єму V₁ до V₂, визначається пло­щею, яка обмежена віссю абсцис, кривою p = f(V) і прямими V₁ i V₂.

Величина роботи A залежить не тільки від початкового і кінцевого станів ті­ла, а й від того, яким є термодинамічний процес, тобто по якій кривій відбувається зміна стану.

106. Теплоємність. Класична молекулярно-кінетична теорія теплоємностей ідеального газу та її обмеженість.

Для характеристики теплових власти­востей газу, як і будь-якого іншого тіла, ко­ристуються особливою величиною - тепло­ємністю.

Теплоємністю тіла називається фізич­на величина, яка числово дорівнює кількості теплоти, яку потрібно надати тілу, щоб підвищити його температуру на один кельвін:

Значення С_Т залежить віл маси тіла, його хімічного складу, термодинамічного стану і виду процесу зміни стану тіла, в якому надходить теплота dQ.

Питомою теплоємністю c назива­ється фізичпа величина, що числово дорів­нює кількості теплоти, яку слід надати одиниці маси цієї речовини для підвищення її температури на 1К :

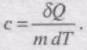
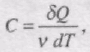Молярною теплоємністю С назива­ється фізична величина, яка числово дорів­нює кількості теплоти, яку треба надати одному молю речовини для підвищення його температури на 1К :

де

v = m/m - кількість молей газу.

Між молярною теплоємністю С і питомою теплоємністю с існує співвідно­шення: С = mс.

Оскільки величина теплоємності газу залежить від умов, при яких йому надається кількість теплоти, то розрізняють теплоєм­ність при сталому об'ємі С_V і теплоємність при сталому тиску C_P. В першому випадку нагрівання газу відбувається при сталому об'ємі, а в другому - при сталому тиску.

Якщо нагрівають газ, то згідно з пер­шим законом термодинаміки dQ = dU + dA,

а для одного моля газу

CdT = dU_m + pdV_m.

Якщо газ нагрівається при сталому об'ємі, то надана газу теплота йде лише на збільшення його внутрішньої енергії:

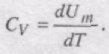
Якщо газ нагрівається при постій­ному тиску, то

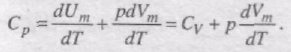
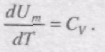Тут враховано, що не залежить від виду процесу, оскільки внутрішня енергія ідеального газу не залежить ні від p, ні від V, а визначається лише температурою. Тому завжди

Згідно з рівнянням Менделєєва - Клапейрона

В результаті

С_p = С_V + R.

Отриманий вираз називається рівнянням Маєра. Воно вказує на те, що С_р завжди більше від С_V на величину універ­сальної газової сталої. Це пояснюється тим, що під час нагрівання газу при сталому тиску потрібна додаткова кількість теплоти на виконання роботи розширення газу.

Оскільки dU_m = i/2 RdT, то

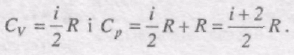
Отримані вирази для С_V i С_р добре збігаються з експериментом для одноатом­них і багатьох двоатомних газів при кімнат­ній температурі (Н₂, N₂, O₂). Однак у Сl₂ C_V = 6/2 R, що неможливо пояснити. У три­атомних газів спостерігаються систематич­ні відхилення від теорії.

Експеримент показав, що теплоєм­ність залежить від температури. Водночас згідно з формулами для С_V i С_р вона стала для даного газу.

Причина розбіжності теорії і експе­рименту для температурної залежності С_V полягає в тому, що закон про рівномірний розподіл енергій між всіма ступенями віль­ності молекул не є правильним, а лише на­ближено застосовується для найпростіших газів, що перебувають при не дуже низьких температурах.

Лише квантова теорія дає змогу поясни­ти температурну залежність теплоємності.

107. Застосування першого закону термодинаміки до ізопроцесів

Ізопроцесами в газах називаються про­цеси, при яких один із основних параметрів стану (V, р, Т) зберігається постійним.

Ізохорний процес (V = соnst, m=соnst).

Діаграма цього процесу в координатах р, V зображається прямою, яка паралельна до осі ординат, де 1-2 - ізохорнне нагрівання, а 1-3 - ізохорне охолодження (рис. 50).

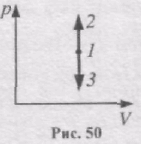При iзохорному процесі газ не виконує роботи над зовнішніми тілами: dА = рdV = 0.

Отже, з першого закону термодинаміки dQ = dU+ +dA для ізохорного процесу випли­ває, що dQ = dU. Оскільки dU_m = C_VdT, то для довільної маси газу

Ізобарний процес (р = соnst, m = const).

Діаграма цього процесу в координа­тах р,V зображається прямою, яка паралель­на до осі V (рис. 51), де 1-2 - ізобарний процес розширення. 1-3 - ізобар­ний стиск.

Робота, яку вико­нує газ при ізобарному розширенні від об'єму V₁ до V₂, дорівнює

де використано рівняння Менделєєва - Клапeйрона.

При ізобарному процесі при надан­ні газу масою m кількості теплоти

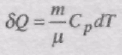
його внутрішня енергія зростає на величину

Газ виконує роботу

Ізотермічний процес (Т = соnst, m = соnst).

Діаграма цього процесу в координатах р, V є гіперболою. 1-3 -ізотермічний стиск, 1-2 - ізотермічне розширення (рис. 52).

Робота газу при ізотермічному розширенні:

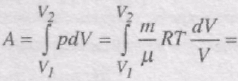
При Т = соnst внутрішня енергія ідеального газу не змінюється, тобто

тобто вся кількість теплоти, надана газу, витрачається на виконання ним роботи про­ти зовнішніх сил:

Робота розширення газу (V₂ > V₁) додатна. У випадку стиску газу (процес 1-3) робота А, що виконується газом, від'ємна, водночас зовнішні сили виконують додатну роботу А' = -А. При цьому Q < 0, тобто теплота від газу відводиться.

108. Адіабатний процес. Застосування першого закону термодинаміки до адіабатного процесу ідеального газу

Адіабатний - це такий процес, який відбувається без обміну теплотою (dQ = 0) між термодинамічною системою і середовищем.

Розглянемо, при яких умовах можна реально здійснити адіабатний процес. Мож­ливо в трьох випадках здійснити процес, який буде адіабатним.

В першому випадку необхідна аді­абатна оболонка, теплопровідність якої дорів­нює нулю. Такою оболонкою може служити посудина Дьюара. В такій посудині з подвій­ними посрібленими стінками, з простору між якими відкачано повітря, передачі теплоти через стінки практично не буде.

Другий випадок адіабатичних про­цесів - це процеси, що відбуваються дуже швидко. При швидкому стиску газу затра­чається робота dА, внаслідок чого збіль­шується внутрішня енергія dU, що викли­кає підвищення температури. При підви­щенні температури деяка кількість теплоти dQ повинна бути передана навколишньому середовищі, що знаходиться при нижчій температурі, але процес теплопередачі ви­магає деякого часу, тому при швидкому стиску теплота не встигає поширитись з даного об'єму.

Третій випадок - це процеси, що відбуваються в дуже великих об'ємах газу, наприклад, в атмосфері. Якщо в атмосфері відбудеться зменшення тиску - розріджен­ня, яке виникає внаслідок атмосферної діяльності, то кількість теплоти, яка повин­на бути передана із навколишнього простору для того, щоб вирівняти температуру, яка понизилась внаслідок адіабатичного розширення, просто не встигне поширитися упродовж значного проміжку часу.

Перший закон термодиниміки у випадку адіабатичного процесу має такий вигляд:

Продиференціювавши рівняння Менделє­єва - Клапейрона, знайдемо вираз для dТ:

де R = С_р - С_V.

Підставивши значення dT у вираз першого закону термодинаміки, отримаємо

де - показник адіабати, або коефіцієнт Пуассона.

Проінтегруємо отриманий вираз:

рV^g = соnst або p₁V^g₁ = p₂V^g₂.

Цей иираз називається рівнянням Пуассона.

Побудуємо графіки рівнянь:

1) рV^g = соnst (адіабата);

2) рV = соnst (ізотерма) (рис. 53).

Диференціюючи рівняння рV=соnst, отримуємо pdV + Vdp = 0, звідси для ізотерми маємо

Диференціюючи рівняння рV^g = соnst,

маємо рgV^g-1dV + V^gdp = 0.

Звідси

Отже, тангенс кута нахилу адіабати в g разів більший, ніж в ізотерми. Це пояснюсгься тим, що при адіабатному стис­ку 1-3 тиск газу збільшується не лише внаслідок зменшення його об'єму, як при ізотермічному стиску, але і підвищенням температури. При адіабатному розширенні газу 1-2 його температура знижується і тому тиск зменшується швидше ніж при iзотермічному розширенні.

Розрахуємо роботу, яку виконує газ при адіабатному процесі 1-2. Вона вимірюється числово площею, заштрихованою на рис. 53. Якщо газ адіабатно розширю­ється від об'єму V₁ до V₂, то його темпе­ратура зменшується від Т₁ до Т₂ і робота розширення iдеального газу

Оскільки.

тому

Якшо використати рівняння адіабат­ного процесу у змінних T, V i T, p, отримуємо

Тоді роботу газу при адіабатному про­цесі можна записати в такому вигляді:

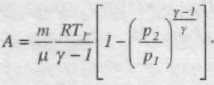
Робота, яка виконується газом при адіабатному розширенні 1-2, менша, ніж при ізотермічному. Це пояснюється тим, що при адіабатичному розширенні відбува­ється охолодження газу, тоді як при ізо­термічному - температура підтримується постійною за рахунок припливу ззовні еквівалентної кількості теплоти.

109. Коловий процес. Теплові двигуни і холодильні машини. Оборотні і необоротні процеси

Коловим процесом (циклом) називається процес, при якому система, про­йшовши через ряд станів, повертається у вихідний стан. На діаграмі процесів цикл зображається замкненою кривою.

Тіло, яке здійснює коловий процес і обмінюється енергією з іншими тілами, називається робочим тілом. Звичайно таким тілом є газ.

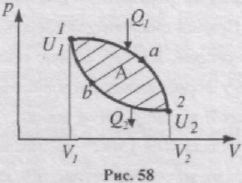
Цикл, який виконує ідеальний газ, можна розбити на процеси розширення (1-2) і стискання (2-1) газу (рис. 58). Робота роз­ширення. яка визначається площею фігури 1а2V₂V₁1, додатнa (dV > 0), робота стиску­вання, що визначається площею фігури 2b1V₁V₂2, від'ємна (dV<0). Робота, яка виконується газом за цикл

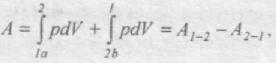
визначається заштрихованою площею, що охоплюється кривою 1a2b1.

Якщо за цикл виконується додатна робота А>0 (цикл виконується за годинни­ковою стрілкою), то він називається прямим. При прямому циклі робочому тілу, надається кількість теплоти Q₁ і тіло виконує роботу розширення А_1-2 . Внутрішня енергія змінюється на величину DU=U₂ - U₁ , де U1 i U2 - внутрішня енергія тіла в стані 1 і 2, відповідно. Потім тіло стискається, над ним виконується робота А^'_2-1 = -A_{2-1 ,} яка менша, ніж А_1-2 , і від нього забирається кількість теплоти Q₂ , яка менша Q₁. Внутрішня енер­гія змінюється на величину - DU. Робота стискування виконується за рахунок викорис­тання частини роботи виконаної при розши­ренні робочого тіла, наприклад, за рахунок кінетичної енергії маховика, що почав оберта­тись при розширенні робочого тіла. За першим законом термодинаміки для про­цесу розширення Q₁ = DU + A_1-2, для процесу стискання:-Q₂ = -DU - A_2-1.

Якщо ці рівняння додати, то отрима­ємо Q₁ - Q₂ = A_1-2 - A_2-1 = A.

Після закінчення циклу тіло повер­тається в свій початковий стан, внутрішня енергія тіла не змінюється. Тому робота циклу може виконуватись лише за рахунок зовніш­ніх джерел, що підводять до тіла теплоту.

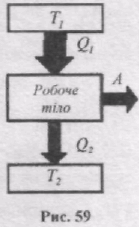Прямий цикл використовується в теп­ловому двигуні, в якому робоче тіло отримує енергію у формі теплоти від зовнішніх джерел і частину її віддає у формі роботи. Тепловий двигун складається з трьох частин: нагрівник, робоче тіло, холодильник (рис. 59). Від термо­стата з вищою темпера­турою Т₁, який назива­ється нагрівником, за цикл відбирається кіль­кість теплоти Q₁, а термостату з нижчою температурою Т₂, який називається холодильником, за цикл передається кількість теплоти Q₂ і виконується робота А = Q₁ - Q₂.

Тепловий двигун характеризується коефіцієнтом корисної дії h, який дорівнює відношенню роботи А, яка виконана тілом за цикл роботи, до кількості теплоти Q₁, що отримало тіло від нагрівника:

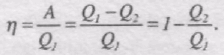
Температура газу при його стискуван­ні повинна бути нижча, ніж при розширенні. Тоді тиск газу у всіх проміжних станах при стиску буде менший, ніж при розширенні, і буде виконано умову А_1-2>А_2-1, необхідну при виконанні двигуном корисної роботи.

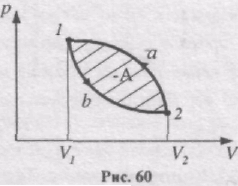
Якщо здійснити цикл проти годинни­кової стрілки, то робота буде та сама за абсо­лютною величиною, але від'ємна (рис. 60):

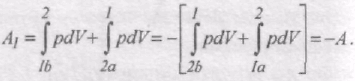
Такий процес називається зворотним. Зворотний цикл використовується в холодильних машинах - періодично діючих установках, в яких за рахунок роботи зовніш­ніх сил теплота переноситься до тіла з вищою температурою (рис. 61). Така машина забирає за цикл від тіла з температурою Т₂, кіль­кість теплоти Q₂ і від­дає тілу при темпера­турі Т₁, кількість теп­лоти Q₁. Над машиною за цикл повинна бути виконана робота A. Кількість відданої теплоти Q₁ дорівнює сумі отриманої кількості теплоти Q₂ і роботи, яку виконали зовнішні сили:

Q₁ = Q₂ +A.

Отже, чистий результат циклу полягає в тому, що тіло з меншою температурою, від якого забирається певна кількість теплоти, охолоджується, а тіло з вищою температурою, якому віддається теплота, нагрівається.

Ефективність холодильної машини характеризуеться її холодильним коефіцієнтом, який дорівнює відношенню віднятої кількості теплоти Q₂ до роботи, яка затра­чається на приведення машини в роботу:

Робочим тілом в холодильній машині слугують пари рідин, які легко киплять: аміак, фреон і ін. Енергія підводиться до машини від електричної мережі. За рахунок цієї енергії відбувається перехід теплоти від холодильної камери до більш нагрітого тіла - до навколишнього середовища.

Оборотним термодинамічним процесом називається така зміна стану сис­теми, яка, будучи проведена у зворотному напрямку, повертає її в початковий стан так, щоб система пройшла через ті самі проміжні стани, що і у прямому процесі, але у зворотній послідовності, а стан тіл поза системою залишився незмінним.

Необоротним називається процес, коли зворотний перехід через ті самі проміжні стани неможливий.

Будь-який рівноважний процес є оборотним.

Оборотні процеси - це до деякої мі­ри ідеалізація реальних процесів. Всі реаль­ні процеси є необоротними.

110. Цикл Карно і його коефіцієнт корисної дії для ідеального газу

Цикл Карно – це цикл ідеальної теплової машини. В ній відсутні втрати на теплопровідність, теплове випромінювання, тертя і т.п.

Цикл Карно встановлює основні співвідношення процесу переходу теплоти від одного тіла до іншого з перетворенням цієї теплоти.

Розглянемо коловий процес, в ре­зультаті якого тепло, відняте від якогось тіла, можна перетворити в роботу і прито­му якнайкраще.

Карно довів теорему: із всіх періо­дично діючих теплових машин, що мають однакові температури нагрівачів і холо­дильників, найбільший ККД мають обо­ротні машини: при цьому ККД оборотних машин, що працюють при однакових тем­пературах нагрівачів і холодильників, до­рівнюють один одному і не залежать від конструкції машини.

Цикл Карно складається з двох ізо­терм і двох адіабат .

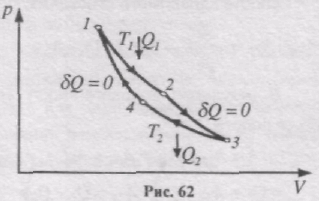Ізотермічне розширення і стиск задані, відповідно, кривими 1-2 і 3-4, адіабатне роз­ширення і стиск-, відповідно, кривими 2-3 і 4-1. Для виконання циклу Карно необхідні термостат з температурою Т₁ (нагрівник) і термостат з температурою Т₂ (холодиль­ник), причому Т₁>Т₂. При проходженні адіабатних ділянок циклу система повинна бути термоізольованою від навколишнього середовища.

Визначимо ККД циклу Карно. При ізотермічному процесі DU=0 і робота роз­ширення газу А₁₂ дорівнює кількості теп­лоти Q₁, що отримав газ від нагрівника:

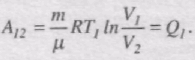
При адіабатному розширенні робо­та виконується за рахунок зміни внутріш­ньої енергії:

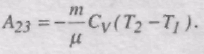
При ізотермічному стисканні газу виконується робота А₃₄ і газ віддає холо­дильнику кількість теплоти Q₂:

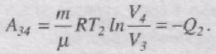
Робота адіабатного стискання:

В результаті колового циклу виконується робота

А = А₁₂ + А₂₃ + А₃₄ + А₄₁ = Q₁ + A₂₃ - Q₂ - A₂₃ = Q₁ - Q₂.

Термічний ККД циклу Карно

Використаємо рівняння адіабат 2-3 і 4-1:

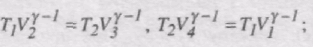
Звідси

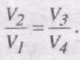
Тоді,

і

Для циклу Карно ККД визнача­ється лише температурами нагрівника і холодильника.

Лекція №41

111. Другий закон термодинаміки

Другий закон термодинаміки вста­новлює напрямок перебігу і характер про­цесів, що відбуваються в природі.

Згідно із Клаузіусом, який дав одне з перших формулювань другого закона, теплота ніколи не може переходити сама собою від тіл з нижчою температурою до тіл з вищою температурою.

Це означає, що для такого переходу: теплоти потрібна затрата роботи зовніш­нього джерела, що здійснюється в холо­дильній машині.

Фізичний зміст другого закону най­більш зрозуміло розкриваєгься у формулюванні Планка: неможливо побудувати таку періодично діючу теплову машину, яка, отримавши ззовні деяку кількість теплоти при довільній температурі, цілком перетворювала би її в механічну роботу і при цьому поверталась би точно у вихідний стан.

Отже, в довільній тепловій машині перетворюється в роботу лише частина отриманої від нагрівника кількість теплоти, тобто A = Q₁ - Q₂. Теплота Q₂ не використовується в машині і розсіюється в навколишньому середовищі. Величина Q₂ завжди досить велика, тому коефіцієнт корисної дії теплової машини h =Q₁ - Q₂/Q₁ завжди значно менший від одиниці.

Із формули ККД теплової машини, яка працює за циклом Карно,

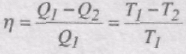
випливає, що Q₂ дорівнювала би нулеві ли­ше в тому випадку, якби температуру робо­чого тіла можна було би довести до тем­ператури абсолютного нуля, яку повинен мати холодильник. ККД реальних теплових машин завжди менший від одиниці.

Вираз для ККД теплової машини, яка працює за циклом Карно, теж є одним з формулювань другого закону:

коефіцієнт корисної дії ідеальної теп­лової машини визначається лише температу­рами нагрівника і холодильника.

Кельвін сформулював другий закон термодинаміки в такому вигляді:

неможливо побудувати теплову ма­шину, яка перетворювала би в роботу тепло­ту найбільш холодного з тіл, що є в системі.

Другий закон термодинаміки вказуе на необоротність процесу перетворення однієї форми передачі енергії - роботи - у другу форму передачі енергії - теплоту. Він стверд­жує, що процес переходу впорядкованого руху тіла як цілого в невпорядкований рух його частинок є необоротним. Упорядкований рух може переходити в неупорядкований без будь-яких додаткових процесів, як це відбува­ється, наприклад, при внутрішньому терті. Перехід же невпорядкованого руху частинок у впорядкований рух тіл можливий лише при умові, що він супроводжується будь-яким компенсуючим процесом.

У тепловій машині, що працює за пря­мим циклом, виконується робота за рахунок підведеної від нагрівника теплоти. Але при цьому частина отриманої теплоти передається холодильнику. Отже, робота за цикл не еквіва­лентна до підведеної теплоти.

У холодильній машині теплота пе­редається віл холодного тіла до гарячого. Проте для здійснення такого процесу не­обхідний компенсуючий процес виконання роботи зовнішніми силами.

112. Ентропія. Ентропія ідеального газу

Формулу коефіцієнта корисної дії ідеальної теплової машини, що працює за циклом Карно

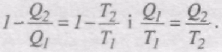приведемо до вигляду

Відношення кількості переданої теп­лоти до температури тепловіддавача або теплоприймача Q/T називається зведеною кількістю теплоти.

Під час виконання циклу Карно при­ведені теплоти при процесах ізотермічного розширення і стиску однакові.

У випадку необоротної теплової машини

і

Тоді, об'єднавши формули для оборот­ної і необоротної теплових машин, маємо:

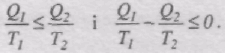
Умовимося кількість теплоти, яка віддана тілу нагрівником, вважати додат­ною, а кількість теплоти, віддану тілом хо­лодильнику, - від'ємною. Тоді

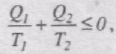
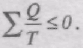причому "=" відповідає оборотним переходам, а "<" - необоротним.

В загальному вигляді

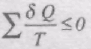При неперервній зміні стану тіла мож­на вважати, що воно входить у теплообмін з неперервним рядом нагрівників і холодиль­ників. Кожен з цих нагрівників і холодильни­ків віддає робочому тілу або отримує від нього нескінченно малі кількості теплоти dQ. Тоді сума

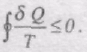перетворюється в інтеграл

Це співвідношення називається рівніс­тю (нерівністю) Клаузіуса.

Розглянемо оборотний цикл 1аnb1 . Запишемо рівність Клаузіуса у виг­ляді суми двох інтегралів:

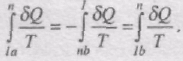
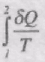Звідси,

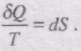Незалежність інтегралу від шляху оборотного переходу між станами 1 і 2 означає, що цей інтеграл виражає зміну деякої функції стану тіла. Підінтегральний вираз dQ/T є повним диференціалом деякої функції, яка визначається лише станом системи і не зале­жить від шляху, яким система прийшла в цей стан. Отже,

Функція стану, диференціал якої є dQ/T , називається ентропією S.

Згідно з визначенням зміна енторопії при оборотному процесі

де підінтегральний вираз і границі інтегрування треба виразити через величини, що характеризують досліджуваний процес. Ця формула визначає ентропію лише з точніс­тю до адитивної сталої, тобто початок відліку ентропії довільний.

Кожний стан тіла характеризується певним значенням ентропії S, яка є повним диференціалом.

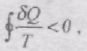Розглянемо цикл 1anb1, частина яко­го 1an необоротна, вона здійснюється нерівноважним процесом, а частина nb1 обо­ротна, виконується рівноважним процесом.

Тоді на основі

тобто інтеграл від по необоротному шляху завжди менший від інтеграла по обо­ротному шляху між тими ж станами.

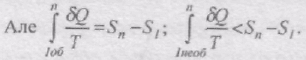
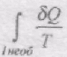
При необоротному процесі менший від зміни ентропії в даному процесі.

Тоді

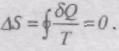Для оборотного рівноважного циклу зміна ентропії

Якщо система виконує необоротний цикл, то ентропія системи зростає: DS > 0.

Ентропія замкненої системи може або зростати, або залишатися постійною.

Оскільки реальні процеси необоротні, то всі процеси в замкненій системі ведуть до збільшення її ентропії - у цьому полягає принцип зростання ентропії. Цей принцип лежить в основі формулювання другого зако­ну термодинаміки: можливі лише такі про­цеси, що відбуваються в макроскопічній сис­темі, які ведуть до збільшення її ентропії.

Знайдемо зміну ентропії у процесах ідеального газу. Оскільки

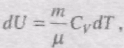
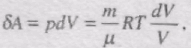
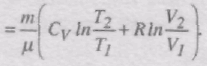
то

Зміна ентропії DS_1à2 ідеального газу при переході його із стану 1 у стан 2 не за­лежить від виду процесу переходу 1à2.

При адіабатному процесі dQ = 0 і DS ³ 0.

Для оборотного адіабатного процесу зміна ентропії дорівнює 0, для необоротного S₂ >S₁ - ентропія тіла зростає.

Оборотний адіабатний процес - ізоентропічний процес.

При ізотермічному процесі T₁ = T₂ і DS = m/mRlnV₂/V₁, при ізохоричному процесі V₁ = V₂ і DS = m/mC_VlnT₂/T₁.

113. Теорема Нернста та її наслідки

У 1906р. термодинаміка збагатилась новим фундаментальним законом, відкритим Нернстом емпіричним шляхом. Цей закон одержав назву теплової теореми Нернста (третій початок термодинаміки)

Зміст теореми Нернста зводиться до двох тверджень:

І. При наближенні до абсолютного нуля ентропія термодинамічної системи прямує до певної конечної межі.

ІІ. Теорема Нернста стверджує, що усі процеси при абсолютному нулі температури, які переводять систему з одного рівноважного стану в інший рівноважний стан, відбуваються без зміни ентропії.

Таким чином теорема Нернста заперечує можливість досягнути температури абсолютного нуля, оскільки всі процеси, які протікають з теплопередачею, супроводжуються зміною ентропії. Це означає, що при S=const процес теплопередачі неможливий,тобто при Т=0 система більше не віддає теплоту, тобто не охолоджується.

Можна сформулювати таке положення:

Не можна досягнути абсолютного нуля температури, відбираючи у тіла теплоту за допомогою кінцевих реальних процесів.

Або, не можна створити машину, яка здатна забрати усю теплоту від тіла, охолодивши його до абсолютного нуля.

Змістовний модуль 9

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. VІI. Утворіть вищий та найвищий ступені порівняння від прислівників із вправи VI.
3. А .Маршалл - основоположник неокласичної теорії.
4. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
5. Альтернативні теорії вартості
6. Альтернативні теорії вартості
7. Альтернативні теорії вартості
8. Альтернативні теорії вартості
9. Альтернативні теорії вартості
10. Альтернативні теорії капіталу
11. Альтернативні теорії макроекономічного регулювання
12. Альтернативні теорії максимізації

Переглядів: 4151