
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Циліндр.
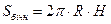 - площа бічної поверхні циліндра.
- площа бічної поверхні циліндра.
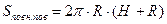 - площа повної поверхні циліндра.
- площа повної поверхні циліндра.
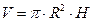 - об’єм циліндра.
- об’єм циліндра.
Розв’язання задач, підготовка до письмової роботи по темі «Площі поверхонь та об’єм циліндра».
№ 1. Дано циліндр. Його осьовий переріз АВСД. Твірна = 3 см, а радіус основи = 2 см. Знайти: 1) ВД – діагональ осьового перерізу; 2) S осьового перерізу; 3) S основи; 4) S бічної поверхні; 5) S повної поверхні.
Дано: циліндр, l = АВ = 3 cм, R = ОА = 2 cм,
Знайти: 1) d = ВД - ? 2)  - ? 3)
- ? 3)  -? 4)
-? 4)  -? 5)
-? 5)  -? 6)
-? 6) 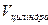 -?
-?
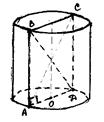
Розв’язання: побудуємо зображення циліндра, його осьового перерізу та діагональ цього перерізу.
1) d = ВД - ?
З D ВАД (Ð А = 90°) за теоремою Піфагора обчислимо ВД.
 АД = 2R = 2ОА = 2×2 = 4 (см), АД = 4 см.
АД = 2R = 2ОА = 2×2 = 4 (см), АД = 4 см.
 ВД = 5 см.
ВД = 5 см.
2)  - ?
- ?
АВСД – осьовий переріз – прямокутник, його площа обчислюється за формулою: 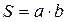 .
.  . Обчислимо
. Обчислимо 

 = 12 см2.
= 12 см2.
3)  -?
-?
Основою циліндра є круг, його площа знаходиться за формулою: 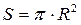 .
.
Обчислимо 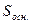
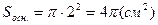 .
.  = 4p см2.
= 4p см2.
4)  -?
-?
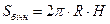 ; Н = АВ = 3 см.
; Н = АВ = 3 см.
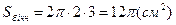 ;
;  = 12p см2.
= 12p см2.
5)  -?
-?
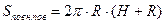 ;
;
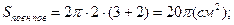
 = 20p см2.
= 20p см2.
6) 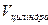 -?
-?
Для знаходження об’єму циліндра скористаємося формулою:  .
.
Обчислимо його,  (см3),
(см3), 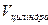 = 12p см3.
= 12p см3.
Відповідь:
- ВД = 5 см.
-
 = 12 см2.
= 12 см2. -
 = 4p см2.
= 4p см2. -
 = 12p см2.
= 12p см2. -
 = 20p см2.
= 20p см2. -
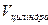 = 12p см3.
= 12p см3.
№ 2.
Дано циліндр. Його осьовий переріз АВСД. Діагональ ВД = 10 см, а довжина кола основи = 6p см. Знайти: 1) S осьового перерізу; 2) S бічної поверхні; 3) S повної поверхні; 4) V циліндра.
Дано: циліндр, АВСД – осьовий переріз, d = ВД = 10 см, с = 6p см.
Знайти: 1)  - ? 2)
- ? 2)  -? 3)
-? 3)  -? 4)
-? 4) 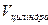 -?
-?
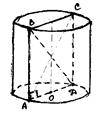 Розв’язання: побудуємо зображення циліндра, його осьового перерізу та діагональ цього перерізу.
Розв’язання: побудуємо зображення циліндра, його осьового перерізу та діагональ цього перерізу.
1)  - ?
- ?
АВСД – осьовий переріз – прямокутник, його площа обчислюється за формулою: 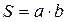 .
. 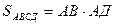 , АВ - ? АД - ?
, АВ - ? АД - ?
а) АД - ?
АД = 2 АО = 2 R, R - ?
За умовою: с = 6p см, за формулою:  .
.
с = с, 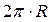 = 6p , R = 3 см, тоді АД = 2×3 = 6(см), АД = 6 см.
= 6p , R = 3 см, тоді АД = 2×3 = 6(см), АД = 6 см.
б) АВ - ?
З D ВАД (Ð А = 90°) за теоремою Піфагора обчислимо АВ.
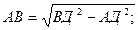
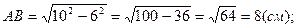 АВ = 8 см.
АВ = 8 см.
Обчислимо  ,
, 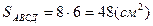 ,
,  = 48 см2.
= 48 см2.
2)  -?
-?
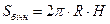 ; Н = АВ = 8 см.
; Н = АВ = 8 см.
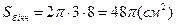 ;
;  = 48p см2.
= 48p см2.
3)  -?
-?
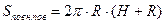 ;
;
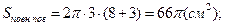
 = 66p см2.
= 66p см2.
4) 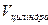 -?
-?
Для знаходження об’єму циліндра скористаємося формулою:  .
.
Обчислимо його, 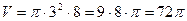 (см3),
(см3), 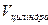 = 72p см3.
= 72p см3.
Відповідь:
-
 = 48 см2.
= 48 см2. -
 = 48p см2.
= 48p см2. -
 = 66p см2.
= 66p см2. -
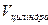 = 72p см3.
= 72p см3.
№ 3.
Висота циліндра = 4 см, а діагональ осьового перерізу утворює з площиною основи циліндра кут 30°. Знайти: 1) діагональ осьового перерізу циліндра; 2) площу основи циліндра; 3) об’єм циліндра.
Дано: циліндр, АВСД – осьовий переріз, Н = СД = 4 см, ÐСАД = 30°.
Знайти: 1) d = АС - ? 2)  -? 3)
-? 3) 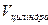 -?
-?
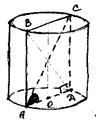 Розв’язання: побудуємо циліндр, його осьовий переріз та діагональ цього перерізу.
Розв’язання: побудуємо циліндр, його осьовий переріз та діагональ цього перерізу.
1) d = АС - ?
З D АДС (Ð Д = 90°) за співвідношенням кутів та сторін в прямокутному трикутнику обчислимо АС і АД.
sin ÐА =  Þ
Þ 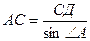 ;
; 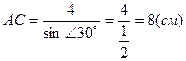 , d = АС = 8 см.
, d = АС = 8 см.
cosÐА =  Þ
Þ 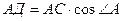 ;
; 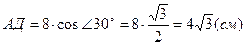 .
.
АД = 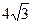 см.
см.
Довжину АД можна знайти іншим способом: через tg ÐA, або ctgÐA, або за теоремою Піфагора.
2)  -?
-?
Основою циліндра є круг, його площа знаходиться за формулою: 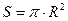 .
.
R = 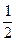 ×АД =
×АД = 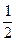 ×
× 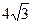 =
= 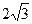 (см)
(см)
Обчислимо 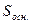
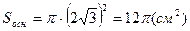 .
.  = 12p см2.
= 12p см2.
3) 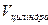 -?
-?
Для знаходження об’єму циліндра скористаємося формулою:  .
.
Обчислимо його, 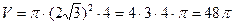 (см3),
(см3), 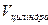 = 48p см3.
= 48p см3.
Відповідь:
- d = АС = 8 см.
-
 = 12p см2.
= 12p см2. -
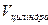 = 48p см3.
= 48p см3.
№ 4.
Діагональ осьового перерізу циліндра = 10 см, і утворює з твірною кут 30°. Знайти: 1) висоту циліндра ; 2) площу основи циліндра; 3) об’єм циліндра.
Дано: циліндр, АВСД – осьовий переріз, d = АС = 10 см , ÐАСД = 30°.
Знайти: 1) Н = СД - ? 2)  -? 3)
-? 3) 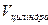 -?
-?
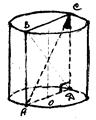 Розв’язання: побудуємо циліндр, його осьовий переріз та діагональ цього перерізу.
Розв’язання: побудуємо циліндр, його осьовий переріз та діагональ цього перерізу.
1) Н = СД - ?
З D АДС (Ð Д = 90°) за співвідношенням кутів та сторін в прямокутному трикутнику обчислимо СД і АД.
cosÐС =  Þ
Þ 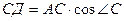 ;
; 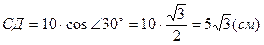 , Н = СД =
, Н = СД =  см.
см.
sin ÐС =  Þ
Þ  ;
; 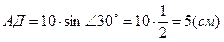 ,
,
АД = 5 см.
Довжину АД можна знайти іншим способом: через tg ÐС, або ctgÐС, або за теоремою Піфагора.
2)  -?
-?
Основою циліндра є круг, його площа знаходиться за формулою: 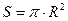 .
.
R = 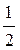 ×АД =
×АД = 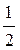 ×5= 2,5(см)
×5= 2,5(см)
Обчислимо 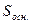
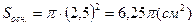 .
.  = 6,25p см2.
= 6,25p см2.
3) 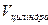 -?
-?
Для знаходження об’єму циліндра скористаємося формулою:  .
.
Обчислимо його, 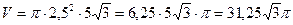 (см3),
(см3),
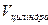 =
= 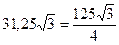 p см3.
p см3.
Відповідь:
- Н = СД =
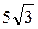 см.
см. -
 = 6,25p см2.
= 6,25p см2. -
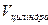 =
= 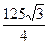 p см3.
p см3.
№ 5.
Радіус циліндра дорівнює 3 см, а кут нахилу діагоналі осьового перерізу до основи дорівнює 60º. Знайдіть об’єм циліндра.
 Дано: циліндр, АВСД – осьовий переріз, R = ОА = 3 см, ÐСАД = 60°.
Дано: циліндр, АВСД – осьовий переріз, R = ОА = 3 см, ÐСАД = 60°.
Знайти: Vциліндра - ?
Розв’язання:
Побудуємо циліндр, його осьовий переріз АВСД та діагональ АС цього перерізу.
Для знаходження об’єму циліндра скористаємося формулою:  , Н = СД - ?
, Н = СД - ?
З D АДС (Ð Д = 90°) за співвідношенням кутів та сторін в прямокутному трикутнику обчислимо СД.
АД = 2ОА = 2×3 = 6 (см).
tg Ð А =  Þ
Þ 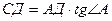 ,
,
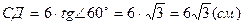 ,
,
Н = 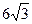 см.
см.
Обчислимо об’єм.
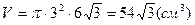 , V =
, V =  см3.
см3.
Відповідь:  см3.
см3.
Письмова робота до теми«Площі поверхонь та об’єм циліндра».
І варіант.
1. Дано циліндр. Його осьовий переріз АВСД. Твірна = 3 см, а довжина кола основи циліндра дорівнює 4p см.
Знайти: 1) S осьового перерізу; 2) S бічної поверхні; 3) S повної поверхні; 4) V циліндра.
2. Діагональ осьового перерізу циліндра = 8 см і утворює з площиною основи циліндра кут 30°.
Знайти: 1) висоту циліндра; 2) площу основи циліндра; 3) об’єм циліндра.
3. Площа основи циліндра дорівнює 36 π см2. Діагональ осьового перерізу утворює з площиною основи циліндра кут 60º. Знайдіть об’єм циліндра.
ІІ варіант.
1. Дано циліндр. Його осьовий переріз АВСД. Діагональ ВД осьового перерізу = 5 см, а площа основи циліндра дорівнює 4 π см2.
Знайти: 1) S осьового перерізу; 2) S бічної поверхні; 3) S повної поверхні; 4) V циліндра.
2. Висота циліндра = 6 см, а діагональ осьового перерізу утворює з твірною кут 60°.
Знайти: 1) діагональ осьового перерізу; 2) площу основи циліндра; 3) об’єм циліндра.
3. Довжина кола основи циліндра дорівнює 12 π см. Діагональ осьового перерізу утворює з площиною основи циліндра кут 30º. Знайдіть об’єм циліндра.
Читайте також:
| <== попередня сторінка | | | наступна сторінка ==> |
| Циліндр. Осьовий переріз циліндра. Переріз циліндра площиною. | | | Конус. Осьовий переріз конуса. Перерізи конуса площинами. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |