
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Закон Гука
Мета
Мета
Мета
Навчальна: ознайомитися з основними характеристиками поступального та обертового рухів тіла, а також кінематичним параметрами найпростіших рухів точки та тіла.
Виховна: виховувати сумлінне відношення до конспектування лекційного матеріалу.
План лекції
1 Поступальний рух твердого тіла та його властивості.
2 Обертовий рух твердого тіла навколо нерухомої осі та його характеристики.
3 Зв’язок між лінійними та кутовими параметрами тіла при обертовому русі.
1 Поступальний рух твердого тіла та його властивості
До найпростіших рухів твердого тіла відносяться поступальний та обертовий рух.
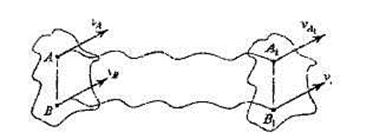
Поступальний рух твердого тіла– це такий рух, при якому пряма, проведена в тілі між будь-якими двома точками, переміщується паралельно самій собі.
|
При поступальному русі всі точки тіла мають однакові швидкості, однакові прискорення й проходять однакові відрізки шляху за однакові проміжки часу. Тому для розрахунків кінематичних параметрів поступального руху тіла використовують формули кінематики точки.
Рівноприскорений рух тіла
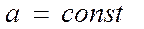
| де а – прискорення, м/с; S – шлях, м; S0 – початковий шлях, м; t – час, с. |
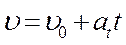
| |

| |

| |
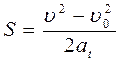
| |

|
Рівномірний рух тіла
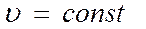
| де u - швидкість, м/с; u0 – початкова швидкість, м/с; |

| |
| Вільне падіння тіла | |

| де u - швидкість, м/с; Н – висота, з якої падає тіло, м; t – час, с; g – прискорення вільного падіння, м/с2; g = 9,81 м/с2 . |

| |

| |
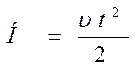
|
2 Рух тіла по колу
Робота більшості машин і механізмів основана на обертальному русі.
Обертовим рухом твердого тіла навколо нерухомої осі називається такий рух, при якому всі точки тіла рухаються по колу, що лежить в площинах, перпендикулярних до осі обертання, із центрами на цій осі.
Обертовий рух характеризується наступними параметрами:
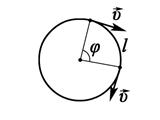
Кутове переміщення – це кут повороту тіла по колу.
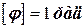

Кутова швидкість – характеризує бистроту зміни кутового переміщення.
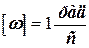
Миттєва кутова швидкість визначається першою похідною від кутового переміщення:
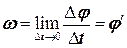
Визначення кутової швидкості через кількість обертів за хвилину:
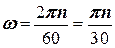 ,
,
де 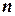 - кількість обертів за хвилину.
- кількість обертів за хвилину.
Якщо кутова швидкість тіла постійна, то рух називається рівномірним рухом по колу.
При цьому: 
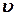 - називається лінійною швидкістю і
- називається лінійною швидкістю і 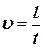 , де
, де  - довжина дуги.
- довжина дуги.
Зв'язок лінійної і кутової швидкостей:  , де
, де  - радіус кола.
- радіус кола.
Визначення лінійної швидкості через кількість обертів за хвилину:
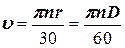
Для тіла, яке рівномірно обертається по колу  , але завжди присутнє
, але завжди присутнє  - нормальне прискорення, яке спрямоване до центра кола і називається доцентровим:
- нормальне прискорення, яке спрямоване до центра кола і називається доцентровим:

Кутове прискорення визначається першою похідною від кутової швидкості:

Рівняння руху: 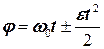
Рівняння швидкості: 
3 Залежність між кутовими та лінійними параметрами тіла, що обертається

| де S – шлях, м; w - кутова швидкість, м/с; at – дотичне прискорення, м/с2; an – нормальне прискорення, м/с2; a - повне прискорення, м/с2. |

| |

| |
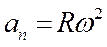
| |
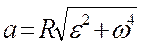
|
Залежність між кутовою швидкістю та частотою обертання
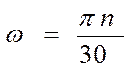
|
Залежність між частотою обертання та кутовою швидкістю
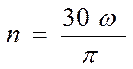
|
Домашнє завдання: Вивчити[І] § 83 – 86.
Контрольні запитання
1 Дайте поняття про кутову швидкість, одиниці її виміру
2 Дайте поняття про кутове прискорення, одиниці його виміру
3 Яке прискорення характерне для точок тіла, що обертається?
4 Чи буде мати прискорення точка, яка рівномірно обертається навколо нерухомої осі?
5 Вкажіть залежність між лінійними та кутовими параметрами точок тіла, що обертається.
6 Вкажіть залежність між кутовою швидкістю та частотою обертання.
7 Вкажіть залежність між частотою обертання та частотою обертання
ЛЕКЦІЯ №9 - РОБОТА ТА ПОТУЖНІСТЬ( 2 години )
Мета
Навчальна: ознайомитися з такими поняттями як робота, потужність, механічний
коефіцієнт корисної дії та формулами для розв’язання задач.
Виховна: виховувати сумлінне відношення до конспектування лекційного матеріалу.
План лекції
1 Робота постійної сили при прямолінійному русі
2 Робота сили тяжіння
3 Потужність
4 Робота та потужність при обертальному русі тіла
Робота постійної сили при прямолінійному русі
Якщо при дії постійної сили F на точку|точку| її переміщення S, то скалярна міра дії сили називається роботою і визначається за формулою:
W = FS cos α
де α — кут|ріг,куток| між напрямком|направленням| дії сили і напрямом|направленням| переміщення.
У СІ робота виражається|виказується,висловлюється| в джоулях: 1 Дж=1Н·1м=1кг·м2/с2.
З|із| формули видно|показно|, що робота — величина скалярна.
При зміні кута|рогу,кутка| α в межах 0° < α < 90° значення cos α > 0. Тому якщо кут|ріг,куток| α — гострий, то робота сили F — позитивна.
При зміні кута|рогу,кутка| α в межах 90° < α < 180° значення cos α < 0. Тому якщо кут|ріг,куток| α — тупий, то робота сили F — негативна|заперечна|.
У випадку, коли напрямок|направлення| дії сили співпадає|збігається| з|із| напрямом|направленням| переміщення (α = 0°), cos α = cos 0° = 1, робота максимально позитивна і рівна
W = FS
У випадку, коли напрямок|направлення| дії сили протилежний напряму|направленню| переміщення (α = 180°), cos α = cos 180° = -1, робота максимально негативна|заперечна| і рівна
W = - FS
При α = 90° значення cos α = cos 90° = 0 і W = 0, тобто робота сили, направленої|спрямованої| перпендикулярно переміщенню точки|точки|, дорівнює нулю.
Якщо на точку діє одночасно декілька сил, то алгебраїчна сума їх робіт, дорівнює роботі рівнодійної сили.
Алгебраїчна сума робіт врівноваженої системи сил, прикладених до точки|точки|, дорівнює нулю.
Сили, що здійснюють|виробляють,справляють| позитивну роботу, називаються рушійними, а що здійснюють |виробляють,справляють| негативну|заперечну| роботу — силами опору.
2 Робота сили тяжіння
Розглянуті|розгледіти| вище три окремі випадки значень роботи сили при α =0°, α =180°, α =90° аналогічні значенням роботи сили тяжіння.
Як відомо з|із| фізики, робота сили тяжіння не залежить від траєкторії руху точки|точки| і завжди рівна добутку|добутку| сили тяжіння на різницю висот в початковому|вихідному| і кінцевому|скінченному| положеннях|становищах|.
Якщо точка М переміщається з|із| положення|становища| М1 в положення|становище| М2, то при будь-якій траєкторії точки|точки| робота сили тяжіння
W = Gh = G( h1 - h2 )= mgh
де h1 — початкова висота точки|точки| над заданим рівнем на Землі;|грунті|
h2 — кінцева|скінченна| висота над тим же рівнем.
При русі точки|точки| вниз робота сили тяжіння позитивна. В цьому випадку сила тяжіння діє як рушійна сила.
При русі точки|точки| вгору|угору| робота сили тяжіння негативна|заперечна|. В цьому випадку сила тяжіння діє як сила опору.
При русі точки|точки| з|із| початкового і кінцевого|скінченного| положень|становищ|, що знаходяться|перебувають| на одному рівні, робота сили тяжіння рівна нулю. Цей випадок аналогічний переміщенню точки|точки| по перпендикулярному напряму|направленню|дододод до лінії дії сили.
Потужність
Скалярна величина що характеризує бистроту|прудкість| виконання роботи, називається середньою потужністю сили.
N = W/ t
У СІ потужність виражається|виказується,висловлюється| у ватах: 1 Вт= 1 Дж/с|із|
Якщо підставити в формулу потужності значення роботи, отримаємо

4 Робота і потужність при обертовому русі тіла
Робота при обертанні тіла рівна добутку|добутку| обертаючого моменту на кут|ріг,куток| повороту:

Потужність при обертанні тіла дорівнює добуткові|добутку| обертального моменту на кутову швидкість:
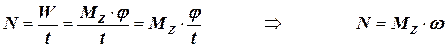
З|із| останньої формули витікає важливе|поважне| слідство|наслідок|:
 — при постійній потужності обертаючий момент обернено пропорційний кутовій швидкості.
— при постійній потужності обертаючий момент обернено пропорційний кутовій швидкості.
5 Механічний коефіцієнт корисної дії
У техніці робота сил звичайно пов'язана з подоланням|здоланням| різних опорів.
Для виконання цієї роботи створюється безліч різноманітних|всіляких| машин і механізмів. Сили опору Fоп, які долає|переборює| будь-яка машина (механізм), можна розділити на дві групи: опори, для подолання|здолання| яких машина або механізм і призначені, і які умовно назвемо|накликатимемо| корисними опорами Fк. оп, і так звані шкідливі опори Fш.оп, які машині (механізму) доводиться вимушено долати|переборювати| попутно з|із| корисними. Роботу по подоланню|здоланню| корисних опорів назвемо|накликатимемо| корисною і позначимо Wк. Роботу по подоланню|здоланню| шкідливих опорів позначимо Wш.
Тоді вся робота, що здійснюється|скоюється,чиниться| машиною або механізмом, W = Wк + Wш звідси Wк = W - Wш
Відношення|ставлення| корисної роботи до всієї роботи називається механічним коефіцієнтом корисної дії (ККД| ) і позначається|значиться| з:
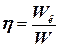
Підставивши в першу з|із| цих формул замість корисної роботи її значення, одержимо
|отримаємо|

Якщо у формулі чисельник і знаменник розділити на t — час, протягом якого працює машина (механізм), то одержимо|отримаємо| формулу ККД| виражену|виказану,висловлену| через відношення|ставлення| потужностей:
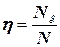
У техніці поширені випадки роботи машин або механізмів при їх послідовному з'єднанні|сполученні,сполуці| один з|із| одним.
При послідовному з'єднанні|сполученні,сполуці| механізмів (машин) їх загальний|спільний| ККД| рівний добутку|добутку| окремих ККД|
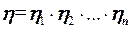
З|із| формули| виходить: чим довший «ланцюг» спільно працюючих механізмів, тим менший її загальний|спільний| ККД|, причому загальний|спільний| ККД| завжди менше самого низького ККД|.
Домашнє завдання:
1Вивчити[І] § 90 -95.
2 Підготуватися до семінарського заняття №2 за темою «Головні поняття з кінематики та динаміки; розв’язання задач з тем 1.6 та 1.7», відповісти на контрольні запитання до семінару у письмовому вигляді.
Контрольні запитання
1 Дайте поняття про роботу та одиниці її виміру.
2 У якому випадку робота позитивна?
3 У якому випадку робота від’ємна?
4 У якому випадку робота дорівнює нулю?
5 Як визначається робота тіла, що обертається?
6 Дайте поняття про потужність та одиниці її виміру.
7 Як визначається потужність тіла, що обертається?
8Дайте поняття про механічний коефіцієнт корисної дії.
9 Як визначається механічний коефіцієнт корисної дії для ланцюга ланок
Зміст
| ЛЕКЦІЯ №10 - ОСНОВИ|становища| ОПОРУ МАТЕРІАЛІВ | |
| ЛЕКЦІЯ № 11 - РОЗТЯГ І СТИСК | |
| ЛЕКЦІЯ № 12 – РОЗРАХУНКИ НА МІЦНІСТЬ ПРИ ДЕФОРМАЦІЇ РОЗТЯГУ ( СТИСКУ) | |
| ЛЕКЦІЯ №13 - КРУЧЕННЯ | |
| ЛЕКЦІЯ № 14 –ЗГИН |
ЛЕКЦІЯ №10 – ОСНОВИ ОПОРУ МАТЕРІАЛІВ(2 години)
Навчальна: дати поняття про види деформованого стану тіл; суть методу перерізів;
внутрішні силові фактори та напруження; геометричні характеристики плоских перерізів.
Виховна: виховувати відповідальність, здібність до аналізу явищ та подій.
План лекції:
1 Початкові|вихідні| поняття;
2 Кваліфікація навантажень;
3 Види деформацій;
4 Основні допущення;
5 Метод перерізів;
6 Напруження|напруження|.
1 Початкові|вихідні| поняття
Опір матеріалів як наука виник в епоху Відродження, коли розвиток техніки, торгівлі, мореплавання|мореплавства|, військової|воєнної| справи|речі| зажадав наукових обґрунтувань, необхідних для споруди крупних морських суден, мостів, гідротехнічних споруд|споруджень| і інших складних конструкцій. Основоположником цієї науки вважають|лічать| італійського ученого Галілея (1564—1642).
Практика показує, що всі частини|частки| конструкцій під дією навантажень деформуються, тобто змінюють|зраджують| свою форму і розміри, а в деяких випадках відбувається|походить| руйнування конструкції.
Опір матеріалів це наука про міцність і деформацію матеріалів і елементів машин і споруд|споруджень|.
У опорі матеріалів розглядаються|розглядуються| методи розрахунку елементів конструкцій на міцність, жорсткість і стійкість.
Міцність- здатність|здібність| матеріалу конструкцій і їх елементів чинити опір дії зовнішніх сил, не руйнуючись.
Розрахунки на міцність дають можливість|спроможність| визначити розміри і форму деталей, що витримують задане навантаження, при найменшій витраті|затраті| матеріалу.
Жорсткість- здатність|здібність| тіла або конструкції чинити опір утворенню деформації.
Розрахунки на жорсткість гарантують, що зміни форми і розмірів конструкцій і їх елементів не перевершать допустимих норм.
Стійкість - здатність|здібність| конструкції чинити опір зусиллям, що прагнуть вивести її з|із| початкового|вихідного| стану рівноваги.
Розрахунки на стійкість запобігають можливості|спроможності| раптової втрати стійкості і викривлення довгих або тонких деталей.
На практиці в більшості випадків доводиться мати справу|річ| з|із| конструкціями складної форми, але|та| їх можна уявити собі такими, що складаються з окремих простих елементів, наприклад, брусів, оболонок (наприклад, резервуари, труби, обшивка кораблів і літаків) і масивів (наприклад, фундаменти, станини верстатів).
Основним розрахунковим елементом в опорі матеріалів є|з'являється,являється| брус. Брус - тіло, поперечні розміри якого малі в порівнянні з довжиною.
Бруси бувають прямолінійні і криволінійні, постійного і змінного перетину. Залежно від їх призначення в конструкції бруси називають колонами, балками, стрижнями|стержнями|.
При деформації тіла під дією зовнішніх сил усередині нього виникають сили пружності, які перешкоджають деформації і прагнуть повернути частинки|частки,часточки| тіла в первинне положення|становище|. Сили пружності виникають в результаті|унаслідок,внаслідок| існування в тілі внутрішніх сил міжмолекулярної взаємодії.
У опорі матеріалів вивчаються деформації тіл і виникаючі при цих деформаціях внутрішні сили.
Після|потім| припинення дії зовнішніх сил викликана|спричинена| ними деформація може повністю або частково зникнути.
Пружність- здатність|здібність| матеріалу усувати деформацію після|потім| припинення дії зовнішніх сил.
Деформація, що зникає після|потім| припинення дії зовнішніх сил, називається пружною; деформація, не зникаюча після|потім| припинення дії зовнішніх сил, називається залишковою або пластичною.
Пластичність- здатність|здібність| матеріалу мати значні залишкові деформації, не руйнуючись при цьому.
Самі матеріали називаються пластичними. До таких матеріалів належать низковуглецева сталь, алюміній, мідь, латунь і ін.
Підкреслимо, що виникнення значних залишкових деформацій в більшості випадків приводить|призводить,наводить| до порушення нормальної роботи конструкції і тому вважається|лічиться| порушенням міцності (як і руйнування).
Матеріали, що мають дуже|дуже| малу пластичність, називаються крихкими. На відміну від пластичних крихкі матеріали руйнуються без помітних залишкових деформацій. До крихких матеріалів відносяться чавун, тверді сплави, скло, цеглина і ін.
2 Кваліфікація навантажень
Навантаження- сукупність зовнішніх сил (активні сили і реакції в'язей), що викликають|спричиняють| деформацію і зміну внутрішніх сил.
Навантаження класифікують за двома ознаками — способу їх прикладення до елементу конструкції і характеру|вдачі| дії на нього.
За способом їх прикладення до тіла навантаження діляться на поверхневі|поверхові,зверхні| і об'ємні. Поверхневі|поверхові,зверхні| сили прикладені до ділянок поверхні і характеризують безпосередню контактну взаємодію даного елементу конструкції з|із| навколишніми|довколишніми| тілами.
У свою чергу|своєю чергою|, поверхневі|поверхові,зверхні| сили діляться на розподілені і зосереджені. В буквальному розумінні зосереджених сил немає, це схематизація. Вважаючи|лічивши| силу зосередженою, умовно нехтують розмірами площі|майдану| взаємодії дотичних тіл.
Сили, розподілені за об'ємом тіла, такі, як сили тяжіння, магнітні сили і сили інерції, відносяться до об'ємних сил.
По характеру|вдачі| дії на тіло навантаження діляться на статичні, повторно-змінні і динамічні (ударні).
Статичні -навантаження, які поступово|повільно| зростають від нуля і, досягнувши деякого кінцевого|скінченного| значення, далі залишаються незмінними.
Прикладом|зразком| статичного об'ємного навантаження може служити система відцентрових сил інерції, що діє на ротор електродвигуна з періоду його розгону і при подальшому|дальшому| рівномірному обертанні.
Повторно-змінним (циклічні) - навантаження, що багато разів змінюються в часі по якому-небудь періодичному закону.
До таких навантажень, зокрема, відносяться сили, що діють на зуби зубчастого|зубчастого| колеса.
Динамічні (ударні) - навантаження, що прикладаються раптово або навіть з|із| деякою швидкістю у момент контакту.
Прикладом|зразком| такого навантаження може служити сила, прикладена до тіла у момент падіння на нього іншого тіла (забивання паль за|із| допомогою копра і т. д.).
3 Види деформацій
З|із| практики відомо, що в процесі експлуатації елементи конструкцій випробовують|відчувають| наступні|слідуючі| основні деформації:
1) розтяг; цю деформацію випробовують|відчувають|, наприклад, канати, троси, цепи|цепи|, шток протяжного верстата;
2) стиск|стискування|; на стиснення|стискування| працюють, наприклад, колони, цегляна|цегельна| кладка, пуансони штампів;
3) зсув|зсув|; деформацію зсуву|зсуву| випробовують|відчувають| заклепки, болти, шпонки, шви зварних з'єднань. Деформацію зсуву|зсуву|, доведену до руйнування матеріалу, називають зрізом. Зріз виникає, наприклад, при різанні ножицями або штампуванні деталей з|із| листового матеріалу;
4) кручення; на кручення працюють вали при обертальному русі. Звичайно деформація кручення супроводжується|супроводиться| іншими деформаціями, наприклад згином|згином|;
5) згин|згин|; на згин|згин| працюють балки, осі, зуби зубчастих|зубчастих| коліс і інші елементи конструкцій.
4 Основні допущення
В процесі виготовлення заготовок і отримання|здобуття| з|із| них готових деталей в матеріалі з'являються|появляються| різні, непіддатливі обліку|урахуванню| поверхневі|поверхові,зверхні| і внутрішні дефекти, наприклад, раковини, тріщини в литих деталях, первинні внутрішні зусилля, викликані|спричинені| нерівномірністю охолодження литих і кованих деталей, нерівномірністю висихання і неоднорідністю деревини, нерівномірністю твердіння і неоднорідністю бетону і т.д.
Оскільки|тому що| закономірності виникнення вказаних явищ встановити неможливо, то в опорі матеріалів приймається ряд|лава,низка| допущень, які дозволяють виключити з|із| розгляду ці явища. В результаті об'єктом вивчення в опорі матеріалів стає не саме реальне тіло, а його наближена модель. Експериментальна перевірка висновків|виведень|, одержаних|отриманих| на підставі приведених нижче допущень, показує, що ці висновки|виведення| цілком|сповна| придатні для застосування|вживання| в практиці інженерних розрахунків.
Допущення про властивості матеріалів:
1 Матеріал однорідний, тобто його властивості не залежать від розмірів виділеного з|із| тіла об'єму|обсягу|. Насправді однорідних матеріалів в природі немає. Наприклад, структура металів складається з безлічі хаотично розташованих|схильних| мікроскопічно дрібних|мілких| кристалів (зерен). Розміри ж елементів конструкцій, що розраховуються, як правило, значно|незмірний| перевищують розміри кристалів, тому допущення про однорідність матеріалу тут повністю застосовне.
2 Матеріал є суцільним середовищем|середою| і безперервно заповнює весь наданий йому об'єм|обсяг|. Це допущення витікає безпосередньо з|із| першого — про однорідність матеріалу — і дозволяє застосовувати математичний аналіз.
3 Матеріал ізотропний, тобто фізико-механічні властивості однакові по всіх напрямах|направленнях|. Таким чином, виділений з|із| суцільного середовища|середи| елемент не залежить від орієнтації щодо|відносно| вибраної системи координат. Метали завдяки своїй дрібнозернистій структурі вважаються|лічаться| ізотропними. Але|та| є багато анізотропних матеріалів. До них відносяться деревина, тканини, фанера, багато пластмас. Проте|однак| в опорі матеріалів розглядаються|розглядуються| в основному матеріали ізотропні.
4 Матеріал в певних межах навантаження тіла має ідеальну пружність, тобто після|потім| зняття навантаження тіло повністю відновлює первинні форми і розміри.
Допущення про характер|вдачу| деформації елементів конструкцій:
1 Принципом початкових розмірів- переміщення точок елементу конструкції, обумовлені його пружними деформаціями, незначні в порівнянні з розмірами самого тіла.
2 Переміщення точок пружного тіла у відомих межах навантаження прямо пропорційні|пропорціональні| силам, що викликають|спричиняють| ці переміщення. Конструкції, для яких справедливо це допущення, називаються такими, що лінійно-деформуються|деформуються|.
3 Принцип незалежності дії сил— результат дії декількох сил не залежить від послідовності навантаження ними даної конструкції і рівний сумі результатів дії кожної сили окремо|нарізно|.
5 Метод перерізів
Для розрахунків деталей машин і споруд|споруджень| на міцність необхідно знати внутрішні сили пружності, що виникають в результаті|унаслідок,внаслідок| дії прикладених до деталей зовнішніх сил.
Щоб правильно розрахувати конструкцію на міцність або на жорсткість, необхідно уміти визначати внутрішні сили по навантаженню. Для виявлення внутрішніх сил в опорі матеріалів застосовується метод перетинів, суть якого полягає в наступному|слідуючому|.
Метод перетинів полягає в тому, що тіло в думках умовно розрізається площиною|плоскістю| на дві частини|частки|, будь-яка з яких відкидається і замість неї до перетину частини|частки|, що залишилася, прикладаються внутрішні сили, що діяли до розрізу; залишена частина|частка| розглядається|розглядується| як самостійне тіло, що знаходиться|перебуває| в рівновазі під дією зовнішніх і прикладених до перерізу внутрішніх сил.
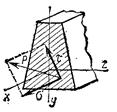
| Розітнемо в думках брус, навантажений врівноваженою системою сил Fi(рис а), поперечним перерізом А на частини|на шматки| I і II і відкинемо одну з них, наприклад частина|частка| II. Щоб зберегти рівновагу частини|частки| бруса (рис б), що залишилася, замінимо дію на неї відкинутої частини|частки| системою сил, які є|з'являються,являються| внутрішніми для цілого бруса і зовнішніми по відношенню до відсіченої частини|частки|. В результаті|унаслідок,внаслідок| приведення цієї системи сил до центру тяжіння перерізу одержимо|отримаємо| головний вектор Fглі головний момент Мгл(рис в). Виберемо систему координатних осей х, у|в,біля|, z так, щоб|так , щоб,таким образом | вісь x була направлена|спрямована| перпендикулярно перерізу, тобто співпадала|збігалася| з|із| віссю бруса, а осі у|в,біля| і z розташовувалися в площині|плоскості| перерізу, причому одна з осей (вісь у|в,біля|) співпадала|збігалася| з|із| її віссю симетрії (рис г). Розклавши головний вектор і головний момент на складові по вибраних осях, одержимо|отримаємо| три сили N, Qy, Qz і три моменти Мк, Му, Мz, які в сукупності називаються внутрішніми силовими факторами|факторами|. | 
|
Ці складові головного вектора разом з головним моментом називатимемо внутрішніми силовими факторами|факторами|.
Шість внутрішніх силових факторів|факторів| разом з відомими зовнішніми силами на частині|частці| бруса, що залишилася, утворюють врівноважену систему сил, для якої можна скласти шість рівнянь рівноваги. Легко бачити, що в кожне з цих рівнянь входить один з невідомих внутрішніх силових факторів|факторів|. Тому, розв`язавши|рішаючи| рівняння, знайдемо:

Складова N головного вектора внутрішніх сил, направлена|спрямована| перпендикулярно площині|плоскості| поперечного перерізу бруса, називається нормальною (подовжньої) силою.
Складові Qy,Qz, що лежать в площині|плоскості| поперечного перерізу, називаються поперечними силами. Складова головного моменту внутрішніх сил момент Мк, що виникає в площині|плоскості| поперечного перетину бруса, називається крутним моментом.Складові моменти Myі Мz, що виникають в площинах|плоскості| перпендикулярних поперечному перерізу бруса, називаються згинаючими моментами.
По аналогії з приведеними найменуваннями внутрішніх силових факторів|факторів| проводиться|виробляється,справляється| класифікація видів навантаження бруса:
1 Якщо в поперечних перерізав бруса виникає тільки|лише| нормальна сила N, то виникає деформація розтягу(сила N направлена|спрямована| від перерізу) або стиску|стискування|(сила N направлена|спрямована| до перерізу).
2 Якщо в поперечному перерізі виникає тільки|лише| момент Мк, то брус в даному перерізі працює на кручення.
3 Якщо в поперечному перерізі виникає тільки|лише| згинаючий момент Мz(або Му), то відбувається|походить| чистий згин|згин|.
4 Якщо в поперечному перетині разом з|поряд з,поряд із| згинаючим моментом (наприклад, Mz) виникає і поперечна сила Qy, то це поперечний згин|згин|.
5 Можливі випадки, коли брус працює на кручення і згин|згин| або розтяг одночасно.
6 Напруження|напруження|
Метод перетинів дозволяє виявити внутрішні силові фактори|фактори|. Але|та| для оцінки міцності необхідно уміти визначати внутрішні сили в будь-якій точці перерізу даного бруса. Тому введемо|запровадимо| числову міру інтенсивності внутрішніх сил — напруження|напруження|.
Розглянемо|розгледимо| брус, до якого прикладене деяке навантаження. Брус під дією навантаження знаходиться|перебуває| в рівновазі. Застосовуючи метод перерізів, розітнемо брус поперечною площиною|плоскістю|, відкинемо ліву частину|частку| бруса, замінимо дію відкинутої частини|частки| на ту, що розглядається|розглядується| системою внутрішніх сил. Виділимо навколо|навкруг,довкола| довільної точки малу площу ΔА|та| (рис а).

Рівнодійну внутрішніх сил в межах цієї площі позначимо ΔF. Відношення|ставлення|
ΔF/ΔA = рср|
називається середнім напруженням|напруженням|. Вектор середнього напруження|напруження| співпадає|збігається| по напряму|направленню| з|із| вектором рівнодійної ΔF.
При поступовому зменшенні площі ΔА змінюються як модуль, так і напрям|направлення| рівнодійної внутрішніх сил ΔF, а отже, вектор рср|поступово наближається до дійсного значення напруження рв заданій точці (рис б). Числове значення цієї напруження виражається|виказується,висловлюється| рівністю

Одиницею напруження служить одиниця сили, що ділиться на одиницю площі|майдану|. У СІ одиниця сили — Н, одиниця площі|майдану| — м2, значить одиниця напруження в цій системі — Н/м2 названа|накликати| паскалем, тобто 1Па=1Н/м2. Паскаль — дуже дрібна|мілка| одиниця напруження, тому більш споживаною одиницею є|з'являється,являється| мегапаскаль|: 1 МПа=106 Па.
Вектор р повного|цілковитої| напруження в точці перерізу можна розкласти на два складових вектора: σ|в,біля|і τ (малюнок).
Вектор σ |в,біля|, направлений|спрямований| перпендикулярно перерізу, називається нормальним напруженням. Вектор τ, що лежить в площині|плоскості| перерізу, називається дотичним напруженням. Оскільки вектори взаємно перпендикулярні, залежність між числовими значеннями напружень р, σ |в,біля|і τ виражається|виказується,висловлюється| формулою
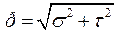
Домашнє завдання: вивчити[І]§ 41 – 44
Контрольні запитання
1 Що вивчає наука «Опір матеріалів» ?
2 Перелічіть механічні властивості матеріалів.
3 Дайте визначення понять: міцність, жорсткість, пружність, пластичність, стійкість.
4 Як ви розумієте поняття: зосереджена сила, розподілене навантаження?
5 В чому полягає сутність методу перерізів?
6 Що називається напруженням та одиниці його виміру?
7 Як діють по відношенню до площини поперечного перерізу повне,нормальне та дотичне напруження?
ЛЕКЦІЯ № 11 - РОЗТЯГ І СТИСК(2 години)
Навчальна: дати поняття про деформацію розтягу та стиску; внутрішні силові фактори, деформацію, закон Гука, умови міцності, побудову епюр повздовжніх сил та нормальних напружень
Виховна: виховувати увагу, формувати аналітичне мислення.
План лекції:
1 Характеристики розтягу і стиску;
2 Епюри та їх побудова;
3 Закон Гука;
4 Коефіцієнт Пуассона;
5 Діаграма розтягування низьковуглецевої сталі;
1 Характеристики розтягу і стиску
Розтягом або стиском|стискуванням| називається такий вид деформації, при якому в будь-якому поперечному перетині бруса виникає тільки|лише| подовжня сила.
Бруси з|із| прямолінійною віссю (прямі бруси), що працюють на розтяг або стиск|стискування|, часто називають стержнями (стрижнями).
Розглянемо|розгледимо| невагомий прямий брус, уздовж|вздовж,уподовж| осі якого діють активні сили F і 2F.


Частини|частки| бруса постійного перетину, знаходяться між поперечними площинами|плоскістю|, в яких прикладені активні або реактивні сили, називатимемо ділянками. Зображений|змальований| на рис брус складається з двох ділянок.
Застосувавши метод перетинів, визначимо подовжні сили N1 і N2 на ділянках. Розітнемо брус на лівій ділянці поперечним перетином 1—1. В усіх точках бруса діятимуть внутрішні розподілені сили, рівнодійна яких визначиться з|із| умови рівноваги однієї з частин|часток| бруса (наприклад, правої від перетину):

Ми бачимо, що для рівноваги залишеної частини|частки| бруса в перетині 1—1 необхідно прикласти тільки|лише| силу N1 направлену|спрямовану| уздовж|вздовж,уподовж| осі, тобто подовжню силу.
Подовжня сила рівнодійна внутрішніх нормальних сил, що виникають в поперечному перетині бруса.
Неважко|скрутно| зрозуміти, що в перетині 2—2 на правій ділянці подовжня сила матиме інше значення: N2 = 2Р.
Таким чином, подовжня сила в поперечному перетині бруса чисельно рівна алгебраїчної сумі зовнішніх сил, розташованих|схильних| по одну сторону перетину.
Надалі розтягуючи (направлені|спрямовані| від перетину) подовжні сили ми вважатимемо|лічитимемо| позитивними, а стискаючи|стискують| (направлені|спрямовані| до перетину) — негативними|заперечними|.
При розтягу і стиску|стискуванні| в поперечних перетинах бруса виникають тільки|лише| нормальні напруги|напруження|, рівномірно розподілені по перетину і обчислювані за формулою
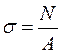
де N — подовжня сила,
А — площа|майдан| поперечного перетину.
При розтягу і стиску|стискуванні| форма перетину на величину напруги|напруження| не впливає.
2 Епюри та їх побудова
Для наглядного зображення розподілу вздовж осі бруса подовжніх сил і нормальних напружень будують графіки - епюрами.
Приклад|зразок|
Побудувати|спорудити| епюри подовжніх сил і нормальних напружень для ступінчастого|східчастого| бруса.
Рішення|розв'язання,вирішення,розв'язування|.
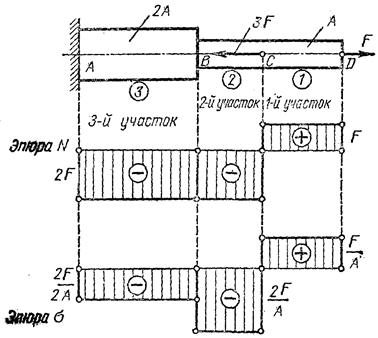
Розіб'ємо брус на ділянки і пронумеруємо їх, як показано на рис. Межами|кордонами| ділянок є|з'являються,являються| точки прикладення|застосування| зовнішніх сил і місця зміни розмірів поперечного перетину. Даний брус складається з трьох ділянок.
Для побудови|шикування| епюри подовжніх сил N під малюнком бруса проводимо вісь або базу епюри, паралельну осі бруса, і штриховими лініями обмежуємо його ділянки.
Величини подовжніх сил в довільному масштабі відкладаємо перпендикулярно осі епюри, причому позитивні значення N (розтяг) відкладаються вгору|угору|, а негативні|заперечні| (стиск|стискування|) — вниз від осі.
Епюра штрихується тонкими лініями, перпендикулярними осі. Лінія штрихування у вибраному масштабі (ордината графіка) дає значення подовжньої сили у відповідному поперечному перетині бруса.
В точках прикладення|застосування| зосереджених сил на епюрі N виходять стрибкоподібні зміни, причому величина «стрибка» рівна модулю прикладеної в перетині бруса зовнішньої зосередженої сили.
Приступимо до побудови|шикування| епюри N. Застосовуючи метод перетинів, встановлюємо, що у всіх поперечних перетинах першої ділянки діє подовжня сила
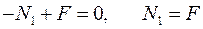 .
.
Відкладаємо вгору|угору| від осі епюри величину F|із| в довільному масштабі і проводимо пряму, паралельну осі епюри. У точці C бруса прикладена сила 3F.
Застосовуючи метод перетинів, встановлюємо, що у всіх поперечних перетинах другої і третьої ділянок діє подовжня сила


також і епюра N2 = N3 буде горизонтальною лінією, розташованою|схильною| на 2F одиниці нижче за вісь епюри.
Очевидно, що значення ординати епюри подовжніх сил під закладенням|запакуванням| рівне реакції закладення|запакування|.
Відмітимо|помітимо|, що, застосовуючи метод перетину, вигідніше розглядати|розглядувати| рівновагу частини|частки| бруса, розташованої|схильної| з боку його вільного кінця, інакше необхідно наперед|заздалегідь| визначати і вводити|запроваджувати| в рівняння рівноваги реакцію закладення|запакування|.
Для побудови|шикування| епюри σ|в,біля| визначимо нормальні напруження на ділянках бруса, беручи відношення|ставлення| значення подовжньої сили (з|із| епюри N) до площі|майдану| поперечного перетину.
Тоді на першій ділянці нормальні напруження будуть
 ,
,
на другому
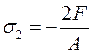 ,
,
на третьому
 .
.
Правила побудови|шикування| епюри σ |в,біля| ті ж, що і для епюри N, включаючи і правило знаків.
В межах кожної з ділянок напруги|напруження| постійні, тому епюра σ |в,біля| на кожній ділянці — пряма, паралельна осі.
Для наочності|наглядності| на епюрах N і σ |в,біля| знаками «+» і «—» наголошуються позитивні і негативні|заперечні| значення ділянок епюр.
Для розрахунків на міцність особливий інтерес представляють|уявляють| ті перетини бруса, в яких напруги|напруження| є|з'являються,являються| по абсолютному значенню максимальними.
Ці перетини є|з'являються,являються| імовірно|приблизно| небезпечними. У нашому прикладі|зразку| такими будуть перетини бруса на другій ділянці.
Уявимо собі прямий брус постійного поперечного перетину A, завдовжки l, жорстко затиснений одним кінцем і навантажений на іншому кінці силою F.

Під дією цієї сили брус подовжиться|довшатиме| на деяку величину Δl, яку назвемо|накликатимемо| абсолютним подовженням|видовженням|.
Відношення|ставлення| абсолютного подовження|видовження| Δl до первинної довжини l назвемо|накликатимемо| відносним подовженням|видовженням| і позначимо ε:
ε =Δl/l.
Відносне подовження|видовження| виражають|виказують,висловлюють| у відсотках|процентах|:
ε =Δl/l ·100%.
Напруження і деформації при розтягу і стисe|стискуванні| зв'язані між собою залежністю, яка називається законом Гука, на ім'я англійського фізика Роберта Гука, що встановив цей закон (1635—1703).
Закон Гука при розтягуванні і стисненні|стискуванні| справедливий лише в певних межах вантаження і формулюється так:
нормальна напруження прямо пропорційне відносному подовженню|видовженню| або скороченню.
Математично закон Гука можна записати у вигляді рівності:
σ = Е ε.
Коефіцієнт пропорційності Е характеризує жорсткість матеріалу, тобто його здатність|здібність| чинити опір пружним деформаціям розтягу або стиску|стискування|, і називається модулем подовжньої пружності або модулем пружності першого роду.
Модуль пружності і напруження виражаються|виказуються,висловлюються| в однакових одиницях:
[E] = [σ]/[ ε] = Па.
Якщо у формулу закону Гука підставити вирази
σ = N/A, ε =Δl/l ,
то одержимо|отримаємо|
Δl = Nl/(EА).
Добуток EА, що стоїть в знаменнику, називається жорсткістю перетину при розтягуванні і стисненні|стискуванні|;
Він характеризує одночасно фізико-механічні властивості матеріалу і геометричні розміри поперечного перетину бруса.
Ця формула читається так: абсолютне подовження|видовження| або скорочення прямо пропорціональне подовжній силі, довжині і обернено пропорційно до жорсткості перетину бруса.
Відношення|ставлення| EA/l називається жорсткістю бруса при розтягуванні або стисненні|стискуванні|.
Приведені вище формули закону Гука застосовні тільки|лише| для брусів або їх ділянок постійного поперечного перетину, виготовлених з|із| одного матеріалу і при постійній подовжній силі.
Для бруса, що має декілька ділянок, що відрізняються матеріалом, розмірами поперечного перетину, величиною подовжньої сили, зміна довжини всього бруса рівна алгебраїчної суми подовжень|видовжень| і скорочень окремих ділянок.
4 Коефіцієнт Пуассона
Поперечні розміри перетину при розтягуванні зменшуються, а при стисненні|стискуванні| збільшуються. Це характерно|вдача| для розтягування і стиснення|стискування| всіх матеріалів.
Дослідним шляхом|колією,дорогою| встановлено|установлено|, що при одноосному розтягуванні або стисненні|стискуванні| відношення|ставлення| відносних поперечної і подовжньої деформацій є для даного матеріалу величина постійна.
Вперше|уперше| залежність між відносною поперечною ε' і відносної подовжньої ε деформаціями була встановлена|установлена| французьким вченим|ученим| Пуассоном (1781—1840).
Ця залежність має наступний|слідуючий| вигляд|вид|:
|ε'| = μ | ε |,
де μ — коефіцієнт поперечної деформації, званий коефіцієнтом Пуассона.
Неважко|скрутно| зрозуміти, що μ — величина безрозмірна.
Коефіцієнт Пуассона, як і модуль пружності першого роду, залежить тільки|лише| від матеріалу і характеризує його пружні властивості. При розтягуванні і стисненні|стискуванні| величину коефіцієнта Пуассона вважають|гадають| однаковою.
5 Діаграма розтягування низьковуглецевої сталі
Механічні характеристики матеріалів, тобто величини, що характеризують їх міцність, пластичність, пружність, твердість, а також пружні постійні E і μ, необхідні конструктору для вибору матеріалів і розрахунків проектованих деталей, визначають шляхом механічних випробувань стандартних зразків|взірців|, виготовлених з|із| досліджуваного матеріалу.

Малюнок 1. Діаграма розтягування низьковуглецевої сталі
Розглянемо|розгледимо| діаграму, отриману|отриману| в процесі найбільш поширеного і важливого|поважного| механічного випробування, а саме випробування на розтягування низьковуглецевої сталі (наприклад, стали Ст3|) при статичному вантаженні.
В процесі цього випробування спеціальний пристрій|устрій| випробувальної машини автоматично викреслює діаграму, що виражає|виказує,висловлює| залежність між розтягуючою силою і абсолютним подовженням|видовженням|, тобто в координатах (F|із|, Δl).
Для вивчення механічних властивостей матеріалу незалежно від розмірів зразка|взірця| застосовується діаграма в координатах «напруження — відносне подовження|видовження|» (σ,|в,біля| ε).
Ці діаграми відрізняються один від одного лише масштабами.
Ця діаграма має наступні|такі| характерні|вдача| точки.
Точка А відповідає межі пропорційності.
Межею пропорційності σпц називається те найбільше напруження, до якого деформації зростають пропорційно навантаженню, тобто справедливий закон Гука(для сталі Ст3 σпр ≈ 200 МПа).
Точка А практично відповідає і іншій межі, яка називається межею пружності.
Межею пружності σпр | називається таке найбільше напруження, до якого деформації практично залишаються пружними.
Точка С|із| відповідає межі текучості.
Межею текучості σт називається таке напруження, при якому в зразку|взірці| з'являється|появляється| помітне подовження|видовження| без збільшення навантаження (Ст3 σт ≈ 240 МПа).
Досягши межі текучості поверхня зразка|взірця| стає матовою, оскільки|тому що| на ній з'являється|появляється| сітка ліній Людерса — Чернова, нахилених до осі під кутом 45°.
Межа текучості є|з'являється,являється| основною механічною характеристикою при оцінці міцності пластичних матеріалів.
Точка В відповідає тимчасовому опору або межі міцності.
Тимчасовим опором σтч | називається умовна напруження, рівне відношенню|ставленню| максимальної сили, яку витримує зразок|взірець|, до первинної площі|майдану| його поперечного перетину (Ст3 σт ≈ 400 МПа).
Досягши тимчасового опору на розтягуваному зразку|взірці| утворюється місцеве звуження — шийка, тобто починається|розпочинається,зачинається| руйнування зразка|взірця|.
У визначенні тимчасового опору мовиться про умовну напругу|напруження|, оскільки|тому що| в перетинах шийки напруги|напруження| будуть більше.
Межею міцності σмц називається тимчасовий опір зразка|взірця|, що руйнується без утворення шийки. Межа міцності є|з'являється,являється| основною механічною характеристикою при оцінці міцності крихких матеріалів.
Точка D відповідає напруженню, що виникає в зразку|взірці| у момент розриву у всіх поперечних перетинах, окрім|крім| перетинів шийки.
Точка М відповідає напруженню, що виникає в найменшому поперечному перетині шийки у момент розриву. Це напруження можна назвати|накликати| напруженням розриву|.
Домашнє завдання: вивчити[І] § 45,46,48 – 50
Контрольні запитання
1 Яка деформація називається розтягом?
2 У якому випадку стержень буде розтягуватися, а коли стискуватися?
3 Який внутрішній силовий фактор виникає при деформаціє розтягу (стиску)?
4 Яке напруження виникає при деформаціє розтягу (стиску)?
5 Чому дорівнює повздовжня сила в будь-якому поперечному перерізі?
6 Сформулюйте закон Гука.
7 Що визначає коефіцієнт пропорційності Е в законі Гука?
8 З якою метою проводять випробування на розтяг та будують діаграму розтягу?
ЛЕКЦІЯ № 12 – РОЗРАХУНКИ НА МІЦНІСТЬ ПРИ ДЕФОРМАЦІЇ РОЗТЯГУ(СТИСКУ)(2 години)
Читайте також:
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- IV. Закони ідеальних газів.
- IV. Закономірності структурно-функціональної організації спинного мозку
- Авілум – “син чоловіка” – повноправна людина, охороні його життя, здоров’я, захисту його майнових інтересів присвячена значна частина законника.
- Аграрне право та законодавство США, Німеччини, Франції, Великої Британії, Ізраїлю, Польщі, Росії
- Аграрні закони України
- Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
- Адаптація законодавства України до законодавства ЄС - один із важливих інструментів створення в Україні нової правової системи та громадянського суспільства
- Адміністративна відповідальність за порушення аграрного законодавства
- Адміністративна відповідальність за порушення земельного законодавства
- Адміністративна відповідальність за порушення податкового законодавства.
- Адміністративна відповідальність осіб, винних в порушенні податкового законодавства
| <== попередня сторінка | | | наступна сторінка ==> |
| Прискорення | | | Приклад перший |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |