• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Параметри вибірки. Розподіл середніх значень.

На експерименті ми отримуємо не генеральні сукупності, параметри яких обговорювалися вище, а вибірки кінцевого об'єму 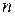. При цьому виникають наступні питання:

1. Як по параметрах вибірки оцінити параметри генеральної сукупності?

2. Яку величину взяти за міру точності результату?

3. Яке співвідношення між довірчими інтервалами і довірчою ймовірністю?

Основні параметри вибірки:

1. Вибіркове середнє - ;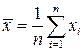

2. Дисперсія вибірки -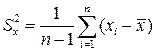

Для різних вибірок (серій вимірювань) одного і того ж об'єму n ми будемо отримувати різні значень як 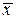, так і 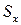. Усереднивши x по великому (в граничному випадку рівному – нескінченності) числу вибірок, ми отримаємо 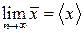. Усереднюючи знайдемо співвідношення : 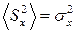. Тому для того, щоб виконалося це співвідношення в знаменнику виразу 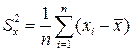повинно стояти не 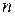, як у виразі (2) а .

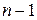Ці результати підказують, що, маючи в розпорядженні одну вибірку, в якості якнайкращого наближення до 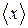слід узяти 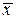, а якнайкращою оцінкою буде .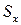

Значення 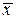- випадкова величина. Узявши 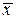як якнайкращу оцінку вимірюваної величини, ми повинні з'ясувати, як поводиться відхилення величини 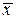від істинного значення, оскільки саме це відхилення, а не розкид окремих вимірювань, визначить похибку остаточного результату експерименту. Теорія і досвід показують, що розкид значень 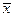залежить від числа вимірювань в кожній серії. Чим більше вимірювань в серіях, тим менше виявляється розкид середніх значень, іншими словами, тим точніше середнє значення відповідає істинному. Якщо число вимірювань 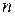скінчене то рівність 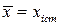уже не буде точною , але і у цьому випадку 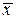є найкращою оцінкою істинного значення х. Позначимо цю знайдену оцінку через :

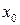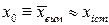
Якщо ми провели невелике число вимірювань 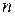і знайшли оцінку істинного значення 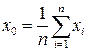то нас буде цікавити якість цієї оцінки.

Оскільки величина 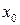є випадковою величиною, тому теж потрібно говорити про розподіл величини 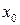тобто про імовірність зустріти різні значення 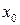. В теорії похибок доведено, що якщо розподіл являєтьсягаусовим,то і розподілоцінки 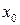буде мати таку ж функціональную форму:

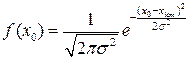
Центр цього розподілу , природно , також лежить при , але величина дисперсії 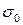буде іншою і визначатиметься за формулою .

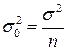Дисперсія середнього із результатів 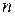вимірювань в 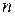разів менше, ніж дисперсія результату окремого вимірювання,отже 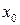- оцінка для x_іст, в 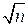разів краща, ніж будь-який з одиничних вимірів .

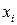Таким чином, для скінченої вибірки дисперсію середнього значення розраховують за за формулою:

.

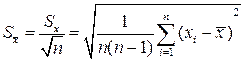Цю величину називають середньоквадратичним відхиленням середнього значення і дана величина може бути прийнята за міру похибки, що міститься в оцінці 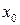. Для більш повного судження про цю похибку вводять поняття довірчої імовірності і довірчого інтервалу, зміст яких розглянемо нижче.

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. IV. Розподіл нервової системи
3. O ексклюзивний розподіл на правах винятковості.
4. V. Розподільний диктант.
5. VII розділ. Маркетингові рішення з розподілу та збуту товару
6. А.2.4.. Розподіл трудомісткості ТО і ПР по видах робіт СТОА
7. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
8. Автоматизація водорозподілу з комбінованим регулюванням
9. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
10. Автоматизація водорозподілу регулювання зі сталими перепадами
11. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
12. Автоматизація водорозподілу регулюванням за верхнім б'єфом

Переглядів: 949