
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Ентропія д. в. в. X
Розв'язання
Скориставшись відповідним рядом розподілу ймовірностей д. в. в. X та Y, знаходимо їх ентропії.
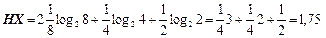 (біт/сим).
(біт/сим).
Ентропія д. в. в. Y  (біт/сим).
(біт/сим).
Побудуємо допоміжну таблицю значень д. в. в. Z=½X-Y½ та їх ймовірностей (табл. 3). Оскільки X та Y – незалежні д. в. в., то сумісна ймовірність випадання пар значень (xi, yj) 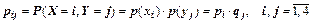 .
.
Таблиця 3
| X | Y | 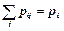
| |||
| 1/8 | |||||
| 1/32 | 1/32 | 1/32 | 1/32 | ||
| 1/8 | |||||
| 1/32 | 1/32 | 1/32 | 1/32 | ||
| 1/4 | |||||
| 1/16 | 1/16 | 1/16 | 1/16 | ||
| 1/2 | |||||
| 1/8 | 1/8 | 1/8 | 1/8 | ||

| 1/4 | 1/4 | 1/4 | 1/4 |
Знайдемо ймовірності системи д. в. в.(Z=j, X=i,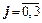 ,
, 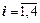 ):
):
P(Z=0, X=1)=1/32, P(Z=1, X=1)=1/32, P(Z=2, X=1)=1/32, P(Z=3, X=1)=1/32; P(Z=0, X=2)=1/32, P(Z=1, X=2)=1/32+1/32=1/16, P(Z=2, X=2)=1/32, P(Z=3, X=2)=0; P(Z=0, X=3)=1/16, P(Z=1, X=3)=1/16+1/16=1/8, P(Z=2, X=3)=1/16, P(Z=3, X=3)=0;P(Z=0, X=4)=1/8, P(Z=1, X=4)=1/8, P(Z=2, X=4)=1/8, P(Z=3, X=4)=1/8.
Побудуємо таблицю розподілу ймовірностей системи д. в. в.(X, Z) (табл. 4).
Таблиця 4
| X | Z | 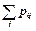
| |||
| 1/32 | 1/32 | 1/32 | 1/32 | 1/8 | |
| 1/32 | 1/16 | 1/32 | 1/8 | ||
| 1/16 | 1/8 | 1/16 | 1/4 | ||
| 1/8 | 1/8 | 1/8 | 1/8 | 1/2 | |
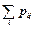
| 1/4 | 11/32 | 1/4 | 5/32 |
Тоді взаємна ентропія д. в. в. Z та X
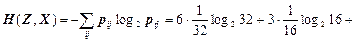
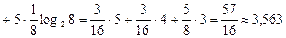 (біт/сим).
(біт/сим).
Скориставшись табл. 3 або табл. 4, побудуємо розподіл ймовірностей д. в. в. Z (табл. 5).
Таблиця 5
| Z | ||||
| pi | 1/4 | 11/32 | 1/4 | 5/32 |
Звідси знаходимо ентропію д. в. в. Z:

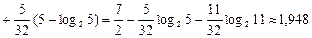 (біт/сим).
(біт/сим).
Кількість інформації, що містить д. в. в. Z стосовно д. в. в. X, знаходимо, скориставшись властивістю 4 кількості інформації і ентропії:
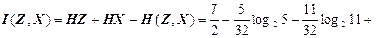
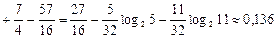 (біт/сим).
(біт/сим).
Побудуємо таблицю розподілу ймовірностей системи д. в. в.(Y, Z) (табл. 6). Для цього, скориставшись табл. 3, обчислимо ймовірності:
P(Z=0, Y=1)=1/32, P(Z=1, Y=1)=1/32, P(Z=2, Y=1)=1/16, P(Z=3, Y=1)=1/8; P(Z=0, Y=2)=1/32, P(Z=1, Y=2)=1/32+1/16=3/32, P(Z=2, Y=2)=1/8, P(Z=3, Y=2)=0; P(Z=0, Y=3)=1/16, P(Z=1, Y=3)=1/32+1/8=5/32, P(Z=2, Y=3)=1/32, P(Z=3, Y=3)=0; P(Z=0, Y=4)=1/8, P(Z=1, Y=4)=1/16, P(Z=2, Y=4)=1/32, P(Z=3, Y=4)=1/32.
Таблиця 6
| Y | Z | 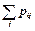
| |||
| 1/32 | 1/32 | 1/16 | 1/8 | 1/4 | |
| 1/32 | 3/32 | 1/8 | 1/4 | ||
| 1/16 | 5/32 | 1/32 | 1/4 | ||
| 1/8 | 1/16 | 1/32 | 1/32 | 1/4 | |
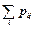
| 1/4 | 11/32 | 1/4 | 5/32 |
Тоді взаємна ентропія д. в. в. Zта Y
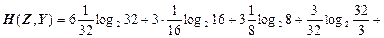
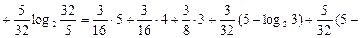
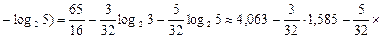
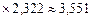 (біт/сим).
(біт/сим).
Отже, кількість інформації, що містить д. в. в. Z стосовно д. в. в. Y
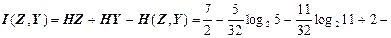
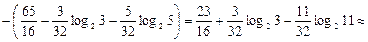
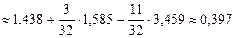 (біт/сим).
(біт/сим).
Відповідь: HX= 1,75 (біт/сим); HY = 2 (біт/сим); 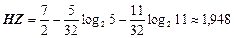 (біт/сим);
(біт/сим);
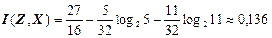 (біт/сим);
(біт/сим);
 (біт/сим).
(біт/сим).
Задачі до розділу 1
1Дискретні випадкові величини (д. в. в.) X1 та X2визначаються підкиданням двох ідеальних тетраедрів, грані яких позначені числами від 1 до 4. Знайти, скільки інформації про д. в. в. X1містить д. в. в. Z=X1*X2, а також ентропію HZ.
2Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z=X+Y стосовно д. в. в. Y. X та Y незалежні д. в. в., задані такими розподілами:
| X | Y | -2 | . | ||||||
| P | 1/8 | 1/8 | 1/4 | 1/2 | P | 3/8 | 5/8 |
3Дискретні випадкові величини (д. в. в.) X1 та X2визначаються підкиданням двох ідеальних тетраедрів, грані яких позначені числами від 1 до 4. Д. в. в. Yдорівнює сумі чисел, що випали при підкиданні цих тетраедрів, тобто Y=X1+X2. Знайти кількість взаємної інформації I(X, Y), ентропії HX1, HY.
4Дискретна випадкова величина (д. в. в.) X визначається кількістю очок, які випадуть при підкиданні грального кубика, а д. в. в. Y=0, якщо кількість очок, що випали, непарна, і Y=1, якщо кількість очок парна. Знайти кількість інформації I(X, Y) та I(Y, Y).
5Скільки інформації про дискретну випадкову величину (д. в. в.) X1 містить д. в. в. Z=(X1+1)2-X2, якщо незалежні д. в. в.X1 та X2 можуть із однаковою ймовірністю набувати значень 0 або 1? Знайти ентропії HX1, HZ. Який характер залежності між д. в. в.X1 та Z?
6Значення дискретних випадкових величин (д. в. в.) X1та X2визначаються підкиданням двох ідеальних монет, а д. в. в. Y – кількість «гербів», що випали на монетах. Знайти ентропії HX1, HY. Скільки інформації про д. в. в. X1 містить д. в. в. Y?
7Дискретні випадкові величини (д. в. в.) X1, X2 залежні й можуть із однаковою ймовірністю набувати значення 0 або 1. Знайти кількість взаємної інформації I(X1, X2), якщо сумісний розподіл ймовірностей системи д. в. в. X1, X2такий:
| X1 | . | ||||
| X2 | |||||
| P | 1/3 | 1/6 | 1/6 | 1/3 |
8Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z=X*Y стосовно X та Y. X, Y – незалежні д. в. в., задані такими розподілами:
| X | Y | -2 | . | ||||||
| P | 1/8 | 1/8 | 1/4 | 1/2 | P | 3/8 | 5/8 |
9Значення дискретних випадкових величин (д. в. в.) X1 та X2 визначаються підкиданням двох ідеальних монет, а д. в. в. Y може набувати два значення: 1, якщо хоча б на одній з монет випав «герб», і 0 - в іншому випадку. Знайти ентропії д. в. в. X1 та Y. Скільки інформації про X1 містить д. в. в. Y?
10Дискретна випадкова величина (д. в. в.) X1 з однаковими ймовірностями може набувати значень -1, 0, 1, а д. в. в. X2 з однаковими ймовірностями – значень 0, 1. X1 та X2– незалежні д. в. в., Y=X12+X22. Знайти кількість взаємної інформації I(Y, X1), I(Y, X2) та ентропії HX1, HX2, HY.
11Знайти ентропії д. в. в. X, Y, Z і кількість інформації, що містить д. в. в. Z=2X+Y стосовно X та Y. X, Y – незалежні д. в. в., задані такими розподілами ймовірностей:
| X | -1 | Y | . | ||||||
| P | 1/4 | 1/2 | 1/4 | P | 1/6 | 2/3 | 1/6 |
12Дискретні випадкові величини (д. в. в.) X1та X2визначаються підкиданням двох ідеальних тетраедрів, грані яких позначені числами від 1 до 4. Знайти, скільки інформації про X1 містить д. в. в. Z=2X1+X2, а також ентропії HZ, HX.
13Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z=X2+Y2 стосовно X та стосовно Y. X, Y – незалежні д. в. в., задані такими розподілами ймовірностей:
| X | Y | . | |||||||||
| P | 1/4 | P | 1/4 |
14Дискретна випадкова величина (д. в. в.) Xз різною ймовірністю може набувати значень від 1до 8. Д. в. в. Yнабуває значення 0, якщо Xпарне, і 1, якщо Xнепарне. Знайти кількість інформації I(Y, X)і ентропію HX, якщо д. в. в. X задана таким розподілом ймовірностей:
| X | . | ||||||||
| P | 0,1 | 0,2 | 0,1 | 0,05 | 0,1 | 0,05 | 0,3 | 0,1 |
15Знайти ентропії дискретних випадкових величин (д. в. в.) X, Y, Z і кількість інформації, що містить д. в. в. Z=½X-Y½ стосовно X та стосовно Y. X, Y – незалежні д. в. в., задані такими розподілами:
| X | Y | . | |||||||||
| P | 1/8 | 1/8 | 1/4 | 1/2 | P | 1/8 | 1/2 | 1/4 | 1/8 |
16Скільки інформації про X1та X2містить дискретна випадкова величина (д. в. в.) Z=X12+X2, якщо незалежні д. в. в. X1, X2можуть з однаковою ймовірністю набувати значення –1 або 1? Знайти ентропії HX1 та HZ.
17Дискретна випадкова величина (д. в. в.) X1може набувати три значення: -1, 0 і 1 з однаковими ймовірностями. Д. в. в. X2 з однаковими ймовірностями може набувати значення 0, 1 і 2. X1 і X2– незалежні, Y=X12+X2. Знайти кількість інформації I(X1,Y), I(X2,Y)і ентропії HX1, HX2, HY.
Розділ 2 ХАРАКТЕРИСТИКИ ДИСКРЕТНОГО КАНАЛУ ПЕРЕДАЧІ ІНФОРМАЦІЇ
2.1 Умовна ентропія
Раніше отримана формула ентропії (1.3) визначає її середньою кількістю інформації, що припадає на одне повідомлення джерела статистично незалежних повідомлень. Така ентропія називається безумовною.
Як відомо з відповідного розділу математичної статистики, мірою порушення статистичної незалежності повідомлень x і у є умовна ймовірністьp(x/y) появи повідомлення xi за умови, що вже вибрано повідомлення yjабо умовна ймовірність появи повідомлення yj, якщо вже отримане повідомлення xi, причому в загальному випадку p(x/y)¹p(y/x).
Умовну ймовірність можна отримати з безумовної ймовірності p(x) чи p(y) та сумісної ймовірності системи в. в. p(x, y) за формулою множення ймовірностей:
p(x, y)=p(x)×p(y/x), (1.7)
p(x, y)=p(y)×p(y/x), (1.8)
звідси
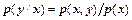 ,
,
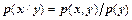 .
.
В окремому випадку для статистично незалежних повідомлень маємо: p(y/x)=p(y), p(x/y)=p(x).
При існуванні статистичної залежності між повідомленнями джерела факт вибору одного з повідомлень зменшує або збільшує ймовірності вибору інших повідомлень до умовних ймовірностей. Відповідно змінюється й кількість інформації, що міститься в кожному з цих повідомлень, згідно з (1.2). Ентропія такого джерела також змінюється відповідним чином, причому обчислюється ентропія за тією самою формулою (1.3), але вже з урахуванням умовних ймовірностей. Така ентропія називається умовною.
2.2 Модель системи передачі інформації
Розглянемо модельсистеми спостереження, перетворення, збору і зберігання інформації, що складається з двох джерел, між повідомленнями яких існує статистичний взаємозв'язок. Нехай джерело X задано моделлю - ансамблем повідомлень {x1, x2, …, xi, …, xk} і рядомрозподілу P(X)їхніх ймовірностей, а джерело Y - ансамблем {y1, y2, …, yj, …, yl} і розподілом P(Y).
Ніяких обмежень на алфавіти X і Y не накладається. Вони можуть навіть збігатися (X=Y). Тоді можна аналізувати і враховувати взаємозв'язок між повідомленнями одного джерела, що рознесені за часом. Найбільш поширеною такою моделлю є послідовності елементарних повідомлень {xi}, умовна ймовірність p(xi/xi-1) кожного з яких залежить тільки від попереднього значення xi-1 за умови появи всіх i-1 повідомлень. Такі послідовності називають ланцюгами Маркова.
Алфавіти X і Y можуть і не збігатися (X¹Y), хоча між їхніми елементами може бути встановлена взаємна відповідність. Джерело X описується моделлю - ансамблем повідомлень {xi}і рядом розподілу P(X). У той самий час джерело X може виступати як об'єкт спостереження для одержувача інформації Y і разом з ним утворювати нове джерело, яке описується моделлю - ансамблем {yj}і розподілом P(Y).Між джерелом X і спостерігачем Y існує канал зв'язку, на який впливають завади, що можуть порушити процес вибору спостерігачем Y повідомлень алфавіту yjÎY, що, у свою чергу, порушує відповідність між повідомленнями xiÎX і yjÎY.
Алфавіти X і Y можуть бути однакового (k=l) і неоднакового (k¹l) об'ємів. Звичайно розглядаються ситуації, коли k=lабо k<l. Система спостереження при k=lмає природне пояснення. Спостерігач Y повинен реагувати повідомленнями yj (j=1, ..., l) на кожний стан джерела X, представлений повідомленням xi (i=1,...,k), при чому кожному повідомленню xi джерела X відповідає повідомлення yjз Y: x1®y1, x2®y2, …, xi®yi, …, xk®yk.
Дана модель показана на рис.1.3, за винятком елемента yl з Y, де l=k+1(жирними лініями показані напрями взаємооднозначної відповідності XÛY).
 . (1.10)
. (1.10)
Статистична залежність джерела X від джерела Y подається матрицею зворотних переходів типу xi¬yj з умовних ймовірностей p(xi/yj):
| P(X/Y)= | X | Y | ||||
| y1 | Y2 | … | yi | … | yk | |
| x1 | p(x1/y1) | p(x1/y2) | … | p(x1/yj) | … | p(x1/yk) |
| x2 | p(x2/y1) | p(x2/y2) | … | p(x2/yj) | … | p(x2/yk) |
| … | … | … | … | … | ||
| xi | p(xi/y1) | p(xi/y2) | … | p(xi/yj) | … | p(xi/yk) |
| … | … | … | … | … | … | |
| xk | p(xk/y1) | p(xk/y2) | … | p(xk/yj) | … | p(xk/yk) |
(1.11)
Матриця (1.11) складається з k розміщених стовпцями варіантів первинних розподілів ймовірностей ансамблю X, що на собі відчуває статистичний вплив повідомлень yj джерела Y. Для кожного такого розподілу виконується умова нормування
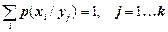 . (1.12)
. (1.12)
Отже, якщо задані ансамбль X і матриця прямих переходів (1.9), то, використовуючи безумовні імовірності P(X)={p(xi)}, за формулою (1.7) можна знайти матрицю сумісних ймовірностей
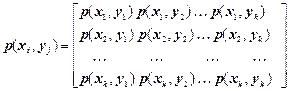 . (1.13)
. (1.13)
Виконавши у (1.13) згортку за i, дістанемо ряд розподілу безумовних ймовірностей P(Y)={p(yj)}, j=1…k:
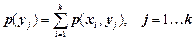 , (1.14)
, (1.14)
а виконавши згортку за j, - розподіл P(X)={p(xi)}, i=1…k:
 . (1.15)
. (1.15)
2.3 Види умовної ентропії
Вирізняють часткову та загальну умовні ентропії джерела повідомлень.
Часткова умовна ентропія- це кількість інформації, що припадає на одне повідомлення джерела X за умови встановлення факту вибору джерелом Y повідомлення yj, або кількість інформації, що припадає на одне повідомлення джерела Y за умови, що відомий стан джерела X:
 , (1.16)
, (1.16)
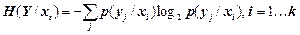 , (1.17)
, (1.17)
де 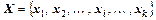 ,
, 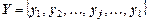 - алфавіти повідомлень; xi - певне повідомлення джерела X, щодо якого визначається часткова умовна ентропія H(Y/xi) алфавіту Y за умови вибору джерелом X повідомлення xi; yj - певне повідомлення джерела Y, щодо якого визначається часткова умовна ентропія H(X/yj) алфавіту X за умови вибору повідомлення yj; i - номер повідомлення з алфавіту X; j - номер повідомлення з алфавіту Y; p(xi/yj), p(yj/xi) – умовні імовірності.
- алфавіти повідомлень; xi - певне повідомлення джерела X, щодо якого визначається часткова умовна ентропія H(Y/xi) алфавіту Y за умови вибору джерелом X повідомлення xi; yj - певне повідомлення джерела Y, щодо якого визначається часткова умовна ентропія H(X/yj) алфавіту X за умови вибору повідомлення yj; i - номер повідомлення з алфавіту X; j - номер повідомлення з алфавіту Y; p(xi/yj), p(yj/xi) – умовні імовірності.
Загальна умовна ентропіявизначається так:
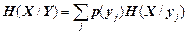 , (1.18)
, (1.18)
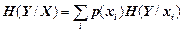 . (1.19)
. (1.19)
Отже, загальна умовна ентропія (1.18) - це середньостатистична кількість інформації (математичне сподівання), що припадає на будь-яке повідомлення джерела X, якщо відомий його статистичний взаємозв'язок з джерелом Y. Так само загальна умовна ентропія (1.19) - це середня кількість інформації, яка міститься в повідомленнях джерела Y за наявності статистичного взаємозв'язку з джерелом X.
З урахуванням (1.16), (1.17) та (1.7), (1.8) вирази (1.18), (1.19) набувають такого вигляду:
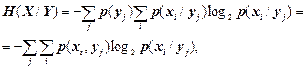 , (1.20)
, (1.20)
 , (1.21)
, (1.21)
де p(xi, yj) - сумісна імовірність появи повідомлень xi, yj; p(xi/yj), p(yj/xi) – їх умовні імовірності.
Властивостіумовної ентропії:
1) якщо джерела повідомлень X і Y статистично незалежні, то умовна ентропія джерела X стосовно Y дорівнюєбезумовній ентропії джерела X і навпаки:
H(X/Y)=H(X), H(Y/X)=H(Y);
2) якщо джерела повідомлень X і Y настільки статистично взаємозв'язані, що виникнення одного з повідомлень спричиняє безумовну появу іншого, то їхні умовні ентропії дорівнюють нулю:
H(X/Y)=H(Y/X)=0;
3) ентропія джерела статистично взаємозалежних повідомлень (умовна ентропія) менша від ентропії джерела незалежних повідомлень (безумовної ентропії):
H(X/Y)<H(X), H(Y/X)<H(Y).
З властивості 3 випливає поняття статистичної надмірності, обумовленої наявністю статистичної залежності між елементами повідомлення:
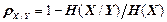 , (1.22)
, (1.22)
де H(X/Y)- загальна умовна ентропія джерела X стосовно джерела Y; H(X) - безумовна ентропія джерела X.
З урахуванням виразу (1.5) загальна статистична надлишковість алфавіту джерела інформації визначається так:
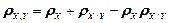 . 1.23)
. 1.23)
У разі малих значень 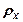 ,
,  статистична надлишковість визначається виразом
статистична надлишковість визначається виразом
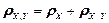 . (1.24)
. (1.24)
Наявність статистичної надмірності джерела інформації дозволяє використовувати кодування інформації, націлене на зменшення її надмірності. Таке кодування називається ефективним,або статистичним.
З метою зменшення статистичної надмірності, обумовленої наявністю статистичної залежності між елементами повідомлення, також застосовується укрупнення елементарних повідомлень. При цьому кодування здійснюється довгими блоками. Імовірнісні зв'язки між блоками менші ніж між окремими елементами повідомлень, і чим довші блоки, тим менша залежність між ними.
Значення укрупнення пояснимо на прикладі буквеного тексту: якщо імовірнісні зв'язки між буквами в будь-якій мові відносно сильні, то між словами вони значно менші, ще менші між фразами, а тим більше між абзацами. Тому кодування цілих слів, фраз, абзаців дозволяє достатньо повно усунути надлишковість, обумовлену імовірнісними зв'язками. Проте при цьому збільшується затримка передачі повідомлень, оскільки спочатку формується блок повідомлення і лише потім виконуються його кодування і передача.
Для зменшення статистичної надмірності, обумовленої нерівноімовірністю повідомленьджерела, використовуються оптимальні нерівномірні коди, в яких завдяки більш раціональній побудові повідомлень вторинного алфавіту досягається значне зменшення надмірності первинного алфавіту.
Ідея побудови оптимальних нерівномірних кодів полягає в тому, що найімовірнішим повідомленням ставляться у відповідність найкоротші кодові комбінації, а найменш імовірним – більш довгі. Проте через нерівномірність таких кодів і їх випадковий характер передача без втрат інформації з постійною швидкістю проходження кодових символів може бути забезпеченою лише за наявності буферного накопичувача з досить великою пам'яттю і, отже, при допустимості великих затримок.
2.4 Ентропія об'єднання двох джерел інформації
Ентропію H(X, Y) об'єднання двох джерел інформації X і Y знаходять через імовірності p(xi, yj) системи випадкових повідомлень xi, yjдля всіх i=1...k, і j=1...l. Для цього складається матриця ймовірностей системи двох статистично залежних джерел
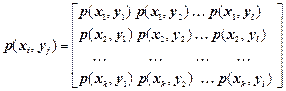 . (1.25)
. (1.25)
Ентропія об'єднання двох джерелщодо конкретного повідомлення можна визначити так:
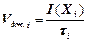 , (1.32)
, (1.32)
де через ti позначено проміжок часу вибору повідомлення xi.
Оскільки джерелом за деякий часовий інтервал вибирається велика кількість повідомлень і в загальному випадку ti¹tj, то продуктивність джерела інформації прийнято характеризувати середнім значенням
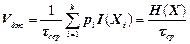 , (1.33)
, (1.33)
де tсер – середній час вибору джерелом одного повідомлення.
Отже, продуктивність джерелаінформаціївизначається середньою кількістю інформації, що виробляється джерелом за одиницю часу.
Повідомлення xi передається по каналу зв'язку спостерігачеві Y, роль якого відіграє приймальний пристрій. Вибір повідомлень yjÎY джерелом Y характеризує процес передачі інформації по каналу зв'язку від джерела X на вихід джерела Y. При цьому взаємна кількість інформації I(X, Y)- це середня кількість інформації про стан джерела X, що міститься в одному повідомленні джерела Y.
Оскільки на вибір кожного повідомлення yj джерелом Y витрачається час t, то швидкість передачі інформаціїпо каналу зв'язку знаходиться за формулою
 . (1.34)
. (1.34)
2.6 Інформаційні втрати при передачі інформації по дискретному каналу зв'язку
Математично канал дискретної інформації описується ансамблем повідомлень на вході {xi},{pi} та йому відповідними йому значеннями на виході {yj}, а також набором умовних ймовірностей p(yj/xi) вибору сигналу yj на виході при передачі сигналу xi.
Задача каналу зв'язку полягає в тому, щоб отримати однозначну відповідність повідомлення yiповідомленню xi, тобто повинна виконуватися умова p(yi/xi)=1 при i=jі p(yj/xi)=0 при i¹j. У цьому випадку канал зв'язку називається каналом без шуму.
Виконання умов використання каналу без шуму означає повний збіг ансамблів X і Y, тобто повний статистичний взаємозв'язок джерелX і Y, тобто
H(X/Y)=H(X), (1.37)
H(Y/X)=H(Y), (1.38)
H(X,Y)= H(X)+H(Y). (1.39)
У даному випадку через сильний вплив завад порушується взаємозв'язок джерел, і інформація від джерела X джерелу Y не передається, отже,
I(X, Y)= 0. (1.40)
У проміжному випадку неабсолютного статистичного взаємозв'язку джерелв каналі визначаються умовною ентропією одного джерела щодо іншого, а кількість переданої інформації - безумовною ентропією джерела і інформаційними втратами за формулою(1.43).
З властивості симетричності взаємної ентропії (1.26)випливає рівність
H(X)+H(Y/X)=H(Y)+H(X/Y). (1.44)
Віднявши від обох частин цієї рівності суму H(X/Y)+H(Y/X), дістанемо
H(X)-H(X/Y)=H(Y)-H(Y/X). (1.45)
Звідси випливає властивість симетричності взаємної інформації
I(X, Y)=I(Y, X).(1.46)
Скориставшись виразами (1.43), (1.44), (1.46), маємо
I(X,Y)=HX-H(X/Y)=HX-(H(X,Y)-HY)=HX+HY-H(X,Y), (1.47)
I(Y,X)=HY-H(Y/X)=HY-(H(Y,X)-HX)=HY+HX-H(Y,X), (1.48)
чим доводяться властивість 4 кількості інформації і повна симетричність виразів (1.47), (1.48).
2.7 Пропускна здатність дискретного каналу. Основна теорема про кодування дискретного джерела
Максимально можлива швидкість передачі інформації по каналу називається пропускною здатністю, або ємністю каналу зв'язку С.
Виходячи з виразів (1.34) і (1.43), дістанемо формулу
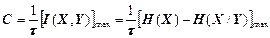 . (1.49)
. (1.49)
Очевидно, що вираз (1.49) досягає максимуму при абсолютній статистичній залежності джерел X, Y, тобто за відсутності або при малому рівні завад. У цьому випадку H(X/Y)=0, і оскільки ентропія максимальна у разі рівноімовірних повідомлень (1.4), то формула (1.49) набуває вигляду:
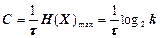 . (1.50)
. (1.50)
Вираз (1.50) визначає пропускну здатність за відсутності завад.
У разі, коли в каналі наявні завади, умовна ентропія на його вході і виході H(X/Y) знаходиться в діапазоні 0 £ H(X/Y) £ H(X). Тоді пропускна здатність каналу визначається за формулою
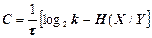 . (1.51)
. (1.51)
При зменшенні рівня завад пропускна здатність каналу C прямує до максимального значення (1.50), а при збільшенні рівня завад – до нуля.
Основна теорема кодування дискретного джерела, сформульована і доведена К. Шенноном1, полягає в такому.
Припустимо, що при передачі інформації використовується канал без шуму. Розглянемо безнадмірні (рівноймовірні) вхідні повідомлення, що характеризуються максимальною ентропією H(X)max. У цьому випадку може бути досягнута максимальна швидкість передачі в каналі
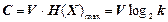 , (1.52)
, (1.52)
де V=1/T; T - тривалість передачі одного елементарного повідомлення (символу) xi; log2 k - максимальна ентропія джерела з алфавітом об'ємом k.
Якщо статистична надлишковість джерела інформації більше нуля, то швидкість передачі інформації по каналу
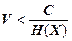 . (1.53)
. (1.53)
Як доведено К. Шенноном1, при будь-якій статистичній надмірності джерела інформації існує такий спосіб кодування повідомлень, при якому може бути досягнута швидкість передачі інформації по каналу без шуму, скільки завгодно близька до його пропускної здатності.Таким чином, умовою узгодженості джерела інформації і каналу передачі є відповідність продуктивності першого пропускній здатності другого.
Теорема Шеннона про кодування дискретного джерелаза відсутності завад1стверджує про таке.
Якщо пропускна здатність каналу без шуму перевищує швидкість створення джерелом повідомлень - його продуктивність, тобто
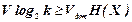 ,
,
то існує спосіб кодування/ декодування повідомлень джерела з ентропією H(X), що забезпечує скільки завгодно високу надійність зіставлення прийнятих кодових комбінацій переданим, інакше - такого способу немає.
За наявності завад в каналі основна теорема кодуванняузагальнюється такою теоремою:
Якщо для будь-якого повідомлення дискретного джерелаXзадана ймовірність його спотворення в каналіe,то для будь-якого e > 0 існує спосіб передачі інформації зі швидкістю
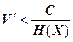 ,
,
скільки завгодно близькою до
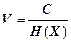 ,
,
при якому ймовірність помилки в каналі буде менше e. Цей спосіб утворює завадостійкий код.
Фано доведена зворотна теорема кодування джерела за наявності завад[2]:
Якщо швидкість передачі інформації по каналу зв'язку з шумом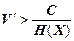 ,то можна знайти такеe > 0,що ймовірність помилки при передачі повідомлення при будь-якому методі кодування/ декодування буде не меншеe (очевидно e зростає із зростанням
,то можна знайти такеe > 0,що ймовірність помилки при передачі повідомлення при будь-якому методі кодування/ декодування буде не меншеe (очевидно e зростає із зростанням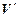 ).
).
Зразки розв'язування задач до розділу 2
Приклад 1Матриця умовних ймовірностей каналу зв'язку між джерелом X і спостерігачем Yмає вигляд
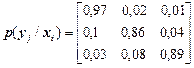 .
.
Знайти часткову та загальну умовні ентропії повідомлень у цьому каналі, якщо задано розподіл ймовірностей джерела Px={0,65; 0,3; 0,05}.
Читайте також:
- Абсолютна ентропія
- Джерело дискретних повідомлень і його ентропія
- Ентропія
- Ентропія дискретної величини
- Ентропія і імовірність
- Ентропія, енергія Гіббса та напрямленість процесів
- Кількість інформації по Шенону. Ентропія, як міра невизначеності інформації, та її властивості
- Самодовільних процесів. Ентропія
- У випадку відкритих систем ентропія може змінюватися як завгодно.
| <== попередня сторінка | | | наступна сторінка ==> |
| Розв'язання | | | Розв'язання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |