Розподіл ймовірностей і його параметри

Нормальний закон розподілу (часто званий законом Гауса) грає виключно важливу роль в теорії ймовірностей і займає серед інших законів розподілу особливе положення. Це – закон розподілу, що найбільш часто зустрічається на практиці. Головна особливість, що виділяє нормальний закон серед інших законів, полягає в тому, що він є граничним законом, до якого наближаються інші закони розподілу при типових умовах, що досить часто зустрічаються.

Нормальний розподіл залежить від двох параметрів - зсуву і масштабу, тобто, є, з математичної точки зору, не одним розподілом, а цілим їх сімейством. Значення параметрів відповідають значенням середнього (математичного сподівання, m) і розсіювання (стандартного відхилення, σ).

Крива розподілу за нормальним законом має симетричний вигляд:

Рис.1. Крива нормального розподілу

Нормальний закон розподілу характеризується щільністю ймовірності виду:

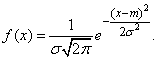
Безпосередньо з формули видно, що центром симетрії розподілу є центр розсіювання m. Це зрозуміло з того, що при зміні знака різниці (x – m) вираз не змінюється. Якщо змінювати центр розсіювання m крива розподілу буде зміщуватися вздовж осі абсцис, не змінюючи своєї форми. Центр розсіювання характеризує положення розподілу на осі абсцис.

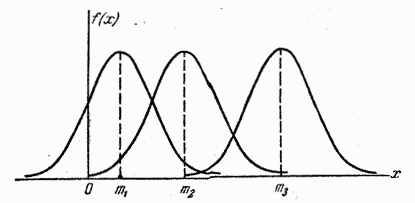
Рис.2. Зміна математичного очікування

Параметр σ характеризує не положення, а саму форму кривої розподілу. Це є характеристика розсіювання. Найбільша ордината кривої розподілу обернено пропорційна σ; при збільшенні σ максимальна ордината зменшується.

Зміна параметра σ рівносильне зміні масштабу кривої розподілу – збільшення масштабу по одній осі і такому ж зменшенню по іншій.

Рис. 3. Зміна розсіювання (дисперсії)

<== попередня сторінка	\|	наступна сторінка ==>
Програмні пакети для проведення розрахунків	\|	Параметричні і непараметричні методи

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.002 сек.