Параметричні і непараметричні методи

В статистці є розмежування на параметричні та непараметричні методи.

Параметричні методи при проведенні певних оцінок містять в собі параметри розподілу даних. Застосовуються головним чином для аналізу нормально розподілених кількісних ознак.

Найпоширенішим параметричним методом оцінки відмінностей між порівнюваними середніми значеннями незалежних вибірок є критерій Стьюдента, або t-критерий.Нульова гіпотеза полягає в рівності генеральних середніх М₁ і М₂, (М₁ – М₂)= 0 сукупностей, з яких були взяті вибірки, або, іншими словами, перевіряється нульова гіпотеза про приналежність двох порівнюваних вибірок однієї і тієї самої генеральної сукупності. T-критерій, що перевіряється, виражається у вигляді відношення різниці відповідних вибіркових середніх до помилки такої різниці, тобто

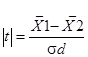або

де σd – стандартна помилка різниці вибіркових середніх значень, σх1, σх2 – стандартні помилки середніх значень порівнюваних вибірок.

Треба звернути увагу, що дисперсія різниці (так само, як і дисперсія суми) двох середніх значень дорівнює сумі дисперсій цих середніх значень.

Для перевірки критерію знак різниці середніх значень не відіграє ролі, тому у формулі для розрахунку тестової статистики береться модуль різниці. Проте знак різниці важливий для інтерпретації результатів порівняння і висновку про перевагу одного з порівнюваних методів. Надалі при порівнянні параметрів у формулах для тестових статистик ми опускатимемо знак модуля.

Гіпотезу про рівність математичних очікувань відкидають, якщо фактично отримана величина t-критерію перевершить або виявиться рівною табличному значенню для прийнятого рівня значимості і числа ступенів свободи. При цьому робиться висновок про наявність статистично значимих відмінностей між середніми значеннями на відповідному рівні значимості.

Формули для розрахунку тестової статистики і числа ступенів свободи дещо розрізняються залежно від рівності або нерівності дисперсій порівнюваних сукупностей. Це питання вимагає уважного розгляду, особливо для вибірок малого об'єму (n < 20).

У разі рівності дисперсій або вибірок достатньо великого об'єму помилка різниці середніх σdвизначається за такими формулами:

для нерівночисельних вибірок при n₁≠n₂

для рівночисельних вибірок при n₁= n₂ формула дещо спрощується:

Число ступенів свободи для випадку рівних дисперсій дорівнює . Якщо хоча б одна з порівнювальних вибірок мала, то спочатку слід перевірити гіпотезу про рівність дисперсій вибірок. Залежно від відповіді на це запитання подальше порівняння середніх арифметичних проводять двома різними способами.

Для перевірки гіпотези про рівність генеральних дисперсій користуються критерієм Фішера. При цьому обчислюють показник Фішера, що дорівнює відношенню більшої вибіркової дисперсії до меншої: 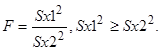Показник Фішера завжди F> 1, а при рівності дисперсій F=1. Чим значніше нерівність, тим більше значення показника і навпаки. Функція F табульована і залежить від чисел ступенів свободи. Якщо обчислене значення F перевищить відповідне табличне значення і гіпотеза про рівність дисперсій буде знехтувана, то це означає, що вибірки були взяті з сукупностей з різними дисперсіями.

Непараметричні методи не враховують розподіл, однак часто потребують трансформації даних. Застосовуються для:

а) аналізу кількісних ознак незалежно від виду їх розподілу;
б) для аналізу якісних ознак.

Найбільш часто вживані непараметричні методи:

· Порівняння двох незалежних вибірок (критерій Манна-Уїтні), проводиться за двома критеріями:

- Критерій знаків

- Критерій Вілкоксона;

· Критерій серій

· Біноміальний критерій

· Критерій Колмогорова-Смірнова для однієї вибірки

· Критерій c² для однієї вибірки

· Порівняння К-незалежних вибірок (критерій Краскала-Уоллеса)

· Порівняння К-залежних вибірок (критерій Фрідмана).

Наведемо U-критерий Уїлкоксона (Манна–Уітні)для перевірки гіпотези про приналежність порівнюваних незалежних вибірок до однієї і тієї самої генеральної сукупності. Гіпотезу перевіряють, розташувавши в узагальнений ряд значення порівнювальних вибірок у зростаючому порядку. Всім значенням отриманого узагальненого ряду привласнюються ранги від 1 до N=n₁+n₂. Для кожної вибірки знаходяться суми рангів R і розраховуються статистики: 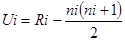для та 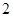- номер вибірки.

Якщо нульова гіпотеза вірна і вибірки були взяті з однієї і тієї самої генеральної сукупності, ми не повинні очікувати переважання спостережень з однієї вибірки на одному з кінців з'єднаного варіаційного ряду, їх значення мають бути достатньо рівномірно розсіяні по всьому узагальненому ряду. Таким чином, дуже великі або дуже малі значення статистики R мають примусити нас засумніватися у справедливості нульової гіпотези. Як тестову статистику вибирають мінімальну величину U і порівнюють її з табличним значенням для прийнятого рівня значимості. Гіпотеза приймається, і відмінності вважаються недостовірними, якщо розраховане значення більше відповідного табличного.

Зазвичай у таблицях наводяться критичні значення даного критерію для об'єму вибірок 20 або 40. У разі вибірок більшого об'єму для перевірки даного критерію застосовується нормальна апроксимація. Тоді критичні значення для критерію U можна розрахувати за формулою:

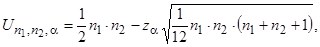
де – критичні значення стандартного нормального розподілу, визначені за таблицями. Треба звернути увагу, що якщо є однакові варіанти, їм привласнюється середній ранг, проте значення останнього рангу має дорівнювати n₁+n₂. Це правило використовують для перевірки правильності ранжирування.

У разі попарно зв'язаних вибірок застосовується Т-критерій Уїлкоксона.При цьому попарні різниці – позитивні і негативні (окрім нульових) в один ряд так, щоб найменша абсолютна різниця (без урахування знака) отримала перший ранг, однаковим величинам привласнюють один ранг. Окремо обчислюють суму рангів позитивних (T+) і негативних різниць (Т-), меншу з двох таких сум без урахування знака вважають тестовою статистикою даного критерію. Нульову гіпотезу приймають на даному рівні значимості, якщо обчислена статистика перевершить табличне значення (число парних спостережень зменшують на число виключених нульових різниць). Таким чином, можна сказати, що якщо нульова гіпотеза вірна, статистики T+ і T – приблизно рівні, порівняно малі або великі значення T-статистик примусять

Література: [1,2,5,16]

<== попередня сторінка	\|	наступна сторінка ==>
Розподіл ймовірностей і його параметри	\|	Тема 3 Метод найменших квадратів: виведення, припущення.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.