
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язання
 Опустимо з вершини призми перпендикуляр до основи. Це і буде висота призми MN, яку необхідно визначити.
Опустимо з вершини призми перпендикуляр до основи. Це і буде висота призми MN, яку необхідно визначити.
Розглянемо 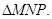 Він прямокутний – за побудовою.
Він прямокутний – за побудовою. 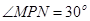 (за умовою).
(за умовою).
Отже, шукана висота MN дорівнюватиме:  (см).
(см).
Рис. 4 Відповідь. 7,5см.

ЗАДАЧІ
1. Намалюйте многогранник, який має 4 грані. Скільки ребер і вершин він має?
2. Намалюйте многогранник, який має 5 граней і 5 вершин. Скільки ребер він має?
3. Намалюйте многогранник, який має 5 граней і 6 вершин. Скільки ребер він має?
4. Скільки діагоналей і діагональних площин має правильна десятикутна призма?
5. Знайдіть градусну міру двогранного кута при бічному ребрі правильної п’ятикутної призми.
6. У трикутній призмі із двогранних кутів між бічними гранями два кути дорівнюють 200 і 1200. Знайдіть третій кут.
7. Побудуйте чотирикутну призму, в основі якої лежить рівнобічна трапеція, а бічні ребра перпендикулярні до основи призми.
8. Побудуйте трикутну призму, у якої бічні ребра не перпендикулярні до площини основи призми. Проведіть висоту призми.
9. Побудуйте трикутну призму, у якій одна із вершин верхньої основи проектуються в центр кола, вписаного в нижню основу призми.
10. Доведіть, що діагональні перерізи призми – паралелограми.
11. Доведіть твердження: якщо діагональні перерізи призми перетинаються, то їх спільний відрізок паралельний бічному ребру.
12. Одне бічне ребро призми перпендикулярне до площини основи. Доведіть, що решта бічних ребер теж перпендикулярна до площини основи.
13. У прямій трикутній призмі сторони основи дорівнюють 10 см, 17 см і 21 см, а висота призми 18 см. Знайдіть площу перерізу, проведеного через бічне ребро і меншу висоту основи.
14. Основа прямої призми – прямокутній трикутник з катетами 3 см і 4 см, а висота призми 5 см. Знайдіть площу повної поверхні призми.
15. У прямій трикутній призмі всі ребра рівні. Бічна поверхня дорівнює 12 м2. Знайдіть висоту.
16. В основі прямої призми лежить ромб із стороною а і гострим кутом α. Більша діагональ призми нахилена до площини основи під кутом β. Знайдіть повну поверхню призми.
17. Знайдіть повну поверхню призми, бічні грані якої є квадратами, а її основою є правильний трикутник, описаний навколо кола радіуса r.
18. У правильній чотирикутній призмі площа основи 144 см2, а висота 14 см. Знайдіть діагональ призми.
19. Бічна поверхня правильної чотирикутної призми дорівнює 32 м2, а повна поверхня 40 м2. Знайдіть висоту.
20. За стороною основи а і бічним ребром b знайдіть повну поверхню правильної призми: а) трикутної; б) чотирикутної; в) шестикутної.
21. Сторона основи правильної чотирикутної призми дорівнює 4 см. Діагональ призми нахилена до площини основи під кутом 600. Знайдіть:
а) висоту призми;
б) площу перерізу призми площиною, яка проходить через діагональ ниж-ньої основи та через кінець мимобіжної з нею діагоналі верхньої основи;
в) кут нахилу площини цього перерізу до площини нижньої основи.
22. Висота правильної трикутної призми дорівнює 6 см, а діагональ бічної грані – 10 см. Знайдіть:
а) сторону основи призми;
б) площу перерізу призми площиною, яка проходить через сторону нижньої основи та через протилежну вершину верхньої основи;
в) кут нахилу площини цього перерізу до площини основи.
23. Відстані між паралельними прямими, які містять бічні ребра похилої трикутної призми, дорівнюють 2 см, 3 см і 4 см, а бічні ребра 5 см. Знайдіть бічну поверхню призми.
24. У похилій трикутній призмі відстані між бічними ребрами дорівнюють 5 см, 12 см і 9 см. Знайти бічне ребро призми, якщо бічна поверхня її дорівнює 260 см2.
25. У похилій трикутній призмі дві бічні грані взаємно перпендикулярні, а їх спільне ребро дорівнює 10 см і знаходиться від інших бічних ребер на відстанях 5 см і 12 см. Знайдіть площу бічної поверхні призми.
26. Потрібно обклеїти шпалерами кімнату розміром 5×4×3 м. Площа вікон і дверей складає 20 % всієї площі стін. Скільки потрібно рулонів шпалер для обклеювання, якщо в рулоні 9 м і ширина його 500 мм ?
27. Скільки треба рулонів шпалер розміром 10×0,5 м, щоб обклеїти кімнату розміром 6×4,8×3,75 м ? Кімната має 4 вікна розміром 1,8×0,75 м. На підклейку витрачається 1 % площі шпалер.
 КОНТРОЛЬНІ ЗАПИТАННЯ
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Що таке двогранний кут (грань кута, ребро кута)?
2. Що таке лінійний кут двогранного кута?
3. Поясніть, що таке тригранний кут (грані і ребра тригранного кута).
4. Що таке многогранник?
5. Який многогранник називається опуклим?
6. Що таке грань опуклого многогранника, ребро, вершина?
7. Що таке призма ( основи призми, бічні грані, ребра)?
8. Призма має n граней. Який многокутник лежить в її основі?
9. Що таке висота призми?
10. Що таке діагональ призми, діагональні перерізи призми?
11. Сформулюйте властивість основ, бічних граней і бічних ребер призми.
12. Яка призма називається прямою, похилою, правильною?
13. Перелічіть властивості прямої і правильної призми.
14. Доведіть теорему про бічну поверхню призми.
15. Чому рівна площа повної поверхні призми?
Тема: Розв’язування задач на властивості паралелепіпеда та знаходження площі його поверхні.
 Мета заняття: формування вмінь розпізнавати і знаходити елементи паралелепіпеда, використовуючи при цьому властивості граней, діагоналей паралелепіпеда, та знаходження площі його бічної і повної поверхні.
Мета заняття: формування вмінь розпізнавати і знаходити елементи паралелепіпеда, використовуючи при цьому властивості граней, діагоналей паралелепіпеда, та знаходження площі його бічної і повної поверхні.
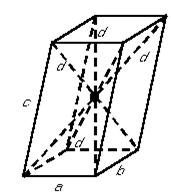 Рис. 5 Рис. 5
| ПАРАЛЕЛЕПІПЕД
Так називається призма, основи якої – паралелограми.
Властивості:
1. Усі грані паралелепіпеда – паралелограми.
2. Протилежні грані паралельні і рівні.
3. Усі чотири діагоналі перетинаються в одній точці і точкою перетину діляться пополам.
4. Точка перетину діагоналей – центр симетрії.
5. Сума квадратів діагоналей дорівнює сумі квадратів усіх ребер:
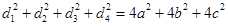
| ||
 Рис. 6 Рис. 6
| Прямий паралелепіпед: паралелепіпед, бічні ребра якого перпендикулярні дооснов. Властивості: 1. Бічні грані – прямокутники. 2. Основи – паралелограми | ||

| Прямокутний паралелепіпед: прямий паралелепіпед, основи якого – прямокутники. Властивості: 1. Усі чотири діагоналі рівні між собою. 2. Квадрат діагоналі дорівнює сумі квадратів ребер, що виходять з однієї вершини: d2=a2+b2+c2. | ||
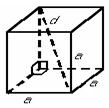
| Куб
Властивості:
1. Усі грані – квадрати.
2. Усі ребра рівні між собою.
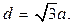 3. 3.
|
| <== попередня сторінка | | | наступна сторінка ==> |
| Задача №1 | | | РОЗГЛЯНЕМО ПРИКЛАДИ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |