• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рівняння площини.

Всяка площина задається у прямокутних координатах лінійним рівнянням виду ax+by+cz+d=0,

де n = (а, b, c) – нормальний вектор, який перпендикулярний до даної площини.

Рівняння сфери.

Означення. Сфера – це геометричне місце (множина) точок, віддалених на задану відстань від одної точки – центра сфери; їх відстань від нього – це радіус сфери.

Рівняння сфери радіуса R з центром в точці О(а, b, с):

(х-а)² + (у-b)²+(z-c)²=R².

Рівняння сфери радіуса R з центром у початку координат:

x²+y²+z²=R².

Література

[3, ст. 231 – 233, 236 – 238]

[4, ст. 127 – 130]

[5, ст. 148 – 150]

[7, ст. 360– 364]

ПРАКТИЧНЕ ЗАНЯТТЯ №10

Задачі на складання рівнянь площини і сфери.

Мета заняття: формування вмінь студентів складати рівняння площини і сфери.

План.

1. Задачі на рівняння площини.

2. Задачі на рівняння сфери.

РОЗГЛЯНЕМО ПРИКЛАДИ

Задача №1 (на рівняння площини).

На пишіть рівняння площини, яка проходить через точку А(1; -3; 5) і паралельна площині, рівняння якої 2х-3у+z+10=0.

Розв’язання. Дана площина перпендикулярна до вектора n=(2; -3; 1). Тому і паралельна їй площина, рівняння якої треба скласти, перпендикулярна до цього вектора, тобто її рівняння має вигляд 2х – 3у + z +d=0. Залишається знайти d. Оскільки точка А (1; -3; 5) належить цій площині, то її координати задовольняють дане рівняння.

Тобто 2×1-3× (-3)+5+d=0, звідки d = -16.

Відповідь. 2х – 3у + z -16=0.

Задача №2 (на рівняння сфери)

Записати рівняння сфери, що проходить через точки А(0; 0; 0), В(4; 0; 0),

С(0; 4; 0), якщо радіус її рівний 3.

Розв’язання. Рівняння сфери з центром О(а; b; с) і радіусом 3 має вигляд

(х - а)² + (у - b)² + (z - c)² =9.

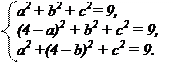Його повинні задовольняти координати точок А, В, С. Числа а, b і с відшукуються з системи трьох рівнянь, що одержуються при підстановці у рівнянні сфери координат трьох даних точок:

Почленно віднімаючи перше рівняння від другого і третього, одержуємо:

16 – 8а = 0, 16 – 8b = 0, звідки а = b = 2.

Значення с відшукується підстановкою знайдених значень а і b у перше рівняння:

4 + 4 + с² = 9, с² = 1, с₁ = 1 , с₂ = -1.

Таким чином, існують дві сфери, що задовольняють умові задачі, їх центри О₁(2; 2; 1) і О₂ (2; 2; -1), а рівняння такі

(х -2)² + (у – 2)² + (z - 1)² = 9 ,

(х -2)² + (у – 2)² + (z + 1)² = 9.

Відповідь. (х -2)² + (у – 2)² + (z - 1)² = 9, (х -2)² + (у – 2)² + (z + 1)² = 9.

Переглядів: 1891