
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Ергодичні стаціонарні процеси
Для багатьох стаціонарних випадкових процесів ймовірнісні характеристики можна одержати шляхом усереднення відповідних величин по одній реалізації досить великої тривалості.
Наприклад, представляється природним за оцінку математичного сподівання  стаціонарного процесу
стаціонарного процесу 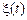 прийняти величину
прийняти величину
 , (23)
, (23)
а за оцінки дисперсії 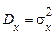 й кореляційної функції
й кореляційної функції 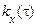 прийняти відповідно величини
прийняти відповідно величини
 , (24)
, (24)
 . (25)
. (25)
Така можливість фізично виправдана тим, що стаціонарний випадковий процес протікає однорідно в часі. Тому одна реалізація досить великої тривалості може містити всі відомості про властивості випадкового процесу. Стаціонарні випадкові процеси, для яких це справедливо, називаються ергодичними. При цьому говорять, що стаціонарний процес має ергодичну властивість.
Стаціонарний процес 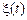 називаєтьсяергодичним у вузькому сенсі, якщо з ймовірністю одиниця всі його ймовірнісні характеристики можуть бути отримані по одній реалізації процесу. Маючи на увазі, що різні характеристики ергодичного процесу зазвичай визначаються шляхом усереднення за часом, можна сказати, що стаціонарний випадковий процес
називаєтьсяергодичним у вузькому сенсі, якщо з ймовірністю одиниця всі його ймовірнісні характеристики можуть бути отримані по одній реалізації процесу. Маючи на увазі, що різні характеристики ергодичного процесу зазвичай визначаються шляхом усереднення за часом, можна сказати, що стаціонарний випадковий процес 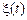 є ергодичним, якщо результати осереднення за часом збігаються з відповідними результатами осереднення за множиною.
є ергодичним, якщо результати осереднення за часом збігаються з відповідними результатами осереднення за множиною.
Процес може бути ергодичним щодо однієї характеристики (параметра) випадкового процесу й не ергодичним щодо інших. У зв'язку із цим можна розглядати поняття ергодичності щодо окремих характеристик процесу. У цьому випадку говорять про ергодичність у широкому сенсі.
Умови ергодичності процесу накладають додаткові вимоги на ймовірнісні характеристики стаціонарного процесу. Тому не всякий стаціонарний процес є ергодичним (у тім або іншому сенсі).
Співвідношення між різними видами випадкових процесів наочно можна представити графічно (рис. 4).

Рис. 4 Співвідношення між різними видами випадкових процесів
Кожний з перерахованих часткових видів випадкових процесів, у свою чергу, можна додатково класифікувати залежно від форми часткових характеристик, що описують процес. Наприклад, за основу класифікації можна прийняти вид кореляційної функції (широкосмугові й вузькосмугові процеси) або характер щільностей ймовірності (нормальні, марківські й інші процеси).
| <== попередня сторінка | | | наступна сторінка ==> |
| Стаціонарні й нестаціонарні процеси | | | Кореляційна функція випадкового процесу |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |