Кореляційна функція випадкового процесу

На практиці часто виявляється достатнім знання тільки математичного сподівання й кореляційної функції досліджуваного випадкового процесу. З'ясуємо основні властивості кореляційної функції.

Нехай доступними для спостереження є два значення випадкового процесу 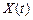: 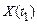і 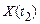. Позначимо відповідні центровані значення через

де 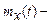математичне сподівання процесу.

У цьому випадку кореляційний момент є функцією моментів часу 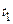й і називається кореляційною функцією процесу

(26)

Нормована кореляційна функція, яка називається коефіцієнтом кореляції, визначається формулою:

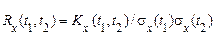, (27)

де 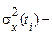дисперсія процесу.

Перелічимо основні властивості нормованої і ненормованої кореляційних функцій.

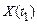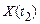1. Якщо для випадкових величин і кореляційна функція дорівнює нулю

то вони є некорельованими; у противному випадку величини є корельованими.

Незалежні величини завжди некорельовані. Однак зворотне твердження в загальному випадку невірно, тому що некорельовані випадкові величини можуть бути залежними.

2. Справедливі співвідношення

. (28)

Випадкові величини, для яких , називаються позитивно корельованими, а негативно корельованими. Позитивна кореляція означає, що при зростанні однієї з них, інша має тенденцію в середньому зростати; негативна кореляція – при зростанні однієї, інша має тенденцію в середньому убувати.

3. Рівності

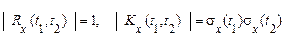(29)

мають місце тоді й тільки тоді, коли існують такі постійні числа 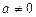й ,що випадкові величини й 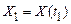з імовірністю одиниця пов'язані лінійною залежністю

Якщо коефіцієнт кореляції досягає одного зі своїх екстремальних значень ±1, то між випадковими величинами й існує строга лінійна залежність. Кожна випадкова величина є лінійною функцією іншої, і обидві величини змінюються в одному напрямку, якщо 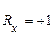, і в різних напрямках, якщо .

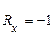4. Кореляційні функції і є симетричними щодо своїх аргументів, тому що спільна щільність імовірності , що входить у вирази для них, є симетричною відносно 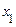й .

Перераховані властивості кореляційних функцій справедливі для будь-яких двох випадкових величин, які можна трактувати як два відліки випадкового процесу, що взяті у два фіксованих моменти часу.

<== попередня сторінка	\|	наступна сторінка ==>
Ергодичні стаціонарні процеси	\|	ЛЕКЦІЯ 14

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.