
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Марківські випадкові процеси
Залежно від того, неперервна або дискретна множина являє собою область можливих значень випадкового процесу 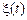 й область визначення параметра
й область визначення параметра 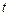 , розрізняють чотири основних види марківських процесів: марківські кола (область значень і область визначення – дискретні множини), марківські послідовності (область значень – неперервна множина, а область визначення – дискретна), дискретні марківські процеси (область значень – дискретна, а область визначення – неперервна множина) і неперервнозначні марківські процеси (область значень і область визначення – неперервні множини). Крім чотирьох основних видів, можливі більш складні (змішані) види марківських процесів.
, розрізняють чотири основних види марківських процесів: марківські кола (область значень і область визначення – дискретні множини), марківські послідовності (область значень – неперервна множина, а область визначення – дискретна), дискретні марківські процеси (область значень – дискретна, а область визначення – неперервна множина) і неперервнозначні марківські процеси (область значень і область визначення – неперервні множини). Крім чотирьох основних видів, можливі більш складні (змішані) види марківських процесів.
Для всіх можливих видів області значень і області визначеннявипадковий процесназивається марківським процесом, якщо при фіксованому  випадкові величини
випадкові величини 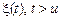 , не залежать від
, не залежать від 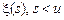 .
.
Таким чином, визначальна властивість всіх видів марківських процесів полягає в тому, що випадковий процес є марківським, якщо для будь-яких 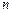 моментів часу
моментів часу 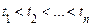 на відрізку
на відрізку  умовна функція розподілу «останнього» значення
умовна функція розподілу «останнього» значення  при фіксованих значеннях
при фіксованих значеннях 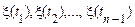 залежить тільки від
залежить тільки від 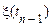 . Наприклад, для трьох моментів часу
. Наприклад, для трьох моментів часу  справедливе співвідношення
справедливе співвідношення
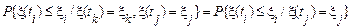 . (50)
. (50)
Тому говорять, що, якщо точно відомий стан марківського процесу в даний момент часу  , то майбутній стан (при
, то майбутній стан (при 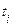 ) не залежить від минулого стану (при
) не залежить від минулого стану (при  ). Як визначення марківського процесу можна також прийняти наступне співвідношення, що має симетричний вигляд щодо часу
). Як визначення марківського процесу можна також прийняти наступне співвідношення, що має симетричний вигляд щодо часу

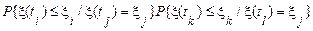 .
.
Такий запис означає, що при фіксованому стані процесу в даний момент часу  майбутній (при
майбутній (при 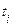 ) і минулий (при
) і минулий (при  ) стани є незалежними.
) стани є незалежними.
З наведених визначень слідує, що n-мірна щільність ймовірності (функція розподілу) марківських процесів, що дає повний опис випадкового процесу, може бути представлена у вигляді
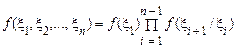 . (51)
. (51)
Це означає, що будь-який n-мірний розподіл марківського процесу може бути знайдений по формулі (51), якщо відомі одномірний розподіл процесу й умовні щільності ймовірності (або ймовірності). Тобто вичерпний опис марківського процесу досягається завданням його двовимірної ЩРІ
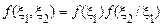 . (52)
. (52)
Розглянемо як приклад коло Маркова, що характеризується тим, що випадковий процес 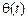 може приймати кінцеве число
може приймати кінцеве число  дискретних значень
дискретних значень  . Значення процесу
. Значення процесу 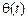 стрибкоподібно змінюється в дискретні моменти часу (
стрибкоподібно змінюється в дискретні моменти часу (  ), які носять випадковий характер, тобто мають місце переходи
), які носять випадковий характер, тобто мають місце переходи 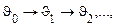 де
де 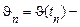 значення процесу через п кроків, а
значення процесу через п кроків, а 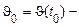 початкове значення. Передбачається, що ймовірнісні закони зміни випадкового процесу на кожному кроці з будь-якого стану
початкове значення. Передбачається, що ймовірнісні закони зміни випадкового процесу на кожному кроці з будь-якого стану  в будь-який інший стан
в будь-який інший стан 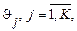 відомі.
відомі.
Характерна властивість простого кола Маркова полягає в тому, що ймовірність значення  процесу в момент часу
процесу в момент часу 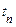 залежить лише від того, яке значення мав процес у безпосередньо попередній момент часу
залежить лише від того, яке значення мав процес у безпосередньо попередній момент часу 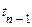 й не залежить від значень процесу в більш ранні моменти часу
й не залежить від значень процесу в більш ранні моменти часу
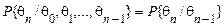 . (53)
. (53)
Складне марківське коло порядку т характеризується тим, що ймовірність нового значення процесу залежить від т значень, безпосередньо йому попередніх. Оскільки складне коло Маркова зводиться до простого для т-мірного вектора, звичайно обмежуються розглядом простого кола. Для простого кола спільні кінцевомірні ймовірності визначаються формулою
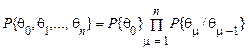 . (54)
. (54)
Умовні ймовірності  називаються ймовірностями переходу зі стану
називаються ймовірностями переходу зі стану  в стан
в стан 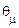 у момент часу
у момент часу 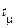 . Основне завдання в теорії простих марківських кіл полягає в визначенні ймовірності значень процесу в довільний момент часу
. Основне завдання в теорії простих марківських кіл полягає в визначенні ймовірності значень процесу в довільний момент часу  . При цьому повинне бути задане початкове значення процесу в момент
. При цьому повинне бути задане початкове значення процесу в момент 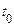 і ймовірнісний закон зміни значень процесу між всіма можливими значеннями (ймовірності переходу).
і ймовірнісний закон зміни значень процесу між всіма можливими значеннями (ймовірності переходу).
Уведемо наступні позначення для вектора-стовпця безумовних і матриці умовних ймовірностей:
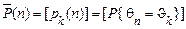 ;
;
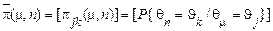 , (55)
, (55)
де 
Величина  є безумовна ймовірність значення
є безумовна ймовірність значення 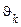 на n-му кроці (у момент часу
на n-му кроці (у момент часу 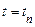 ), а умовна ймовірність
), а умовна ймовірність  визначає ймовірність значення
визначає ймовірність значення 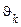 при
при  , якщо в більш ранній момент часу
, якщо в більш ранній момент часу  значення процесу дорівнювало
значення процесу дорівнювало 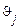 .
.
Уведені ймовірності ненегативні й задовольняють умові нормування
 (56)
(56)
 . (57)
. (57)
На підставі правила повної ймовірності для уведених ймовірностей можна написати рівняння Маркова
 , (58)
, (58)
 . (59)
. (59)
Розписуючи послідовно формулу (59), одержимо
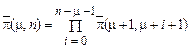 . (60)
. (60)
Звідси видно, що для визначення матриці 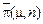 при всіх
при всіх 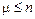 достатньо знати послідовність матриць однокрокових ймовірностей переходу.
достатньо знати послідовність матриць однокрокових ймовірностей переходу.
З урахуванням співвідношень (58) – (60) і (54) робимо висновок, що для повного ймовірнісного опису простого кола Маркова необхідно знати ймовірності початкового стану й послідовність матриць ймовірностей переходу.
Приклад. Нехайсистема зв'язку передає двійкові символи 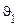 й
й 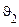 . Кожний переданий символ проходить через кілька каскадів, у кожному з яких вихідний символ з імовірністю
. Кожний переданий символ проходить через кілька каскадів, у кожному з яких вихідний символ з імовірністю 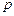 відтворюється вірно й з імовірністю
відтворюється вірно й з імовірністю  переходить в іншій. Потрібно визначити ймовірність того, що якщо на виході n-го каскаду спостерігається символ
переходить в іншій. Потрібно визначити ймовірність того, що якщо на виході n-го каскаду спостерігається символ 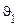 , то на вході був той же символ.
, то на вході був той же символ.
Нехай 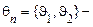 символ на виході n-го каскаду. Тоді послідовність
символ на виході n-го каскаду. Тоді послідовність  є коло Маркова з ймовірностями початкових станів
є коло Маркова з ймовірностями початкових станів  ,
,  , де
, де 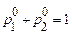 , і матрицею ймовірностей переходу
, і матрицею ймовірностей переходу
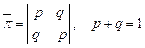 .
.
У загальному випадку на підставі теореми множення ймовірностей можемо записати
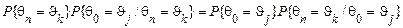
або 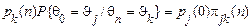 .
.
Звідси  .
.
При 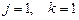 , одержуємо шуканий результат
, одержуємо шуканий результат
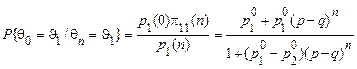 .
.
Як найпростіший марківський процес можна трактувати постійну величину  , для якої
, для якої
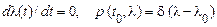 .
.
У такому тривіальному випадку  й
й  .
.
Основну роль при формуванні більш складних марківських процесів грає процес Вінера.
Вінерівський процес 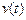 визначається через білий гауссівський шум
визначається через білий гауссівський шум  за допомогою диференціального рівняння
за допомогою диференціального рівняння
 , (61)
, (61)
де 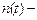 гауссівський стаціонарний процес із нульовим математичним сподіванням і дельтоподібною кореляційною функцією
гауссівський стаціонарний процес із нульовим математичним сподіванням і дельтоподібною кореляційною функцією
 .
.
Рівняння (61) можна інтерпретувати і як визначення білого шуму через вінерівський процес
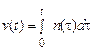 або
або 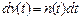 . (62)
. (62)
Оскільки процес 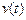 виражається через білий гауссівский шум, тому вінерівский процес є гауссівским.
виражається через білий гауссівский шум, тому вінерівский процес є гауссівским.
З (62) слідує, що
 ,
,

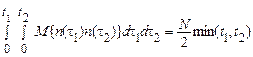 .
.
Одномірна щільність ймовірності має вигляд
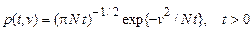 . (63)
. (63)
Отже, вінерівский процес 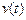 є гауссівським нестаціонарним процесом з нульовим математичним сподіванням і дисперсією, пропорційною часу. Реалізації цього процесу з зростанням часу усе більш й більш розкидані (розпливаються уздовж осі
є гауссівським нестаціонарним процесом з нульовим математичним сподіванням і дисперсією, пропорційною часу. Реалізації цього процесу з зростанням часу усе більш й більш розкидані (розпливаються уздовж осі 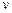 щодо свого нульового математичного сподівання), тому його часто називають дифузійним процесом.
щодо свого нульового математичного сподівання), тому його часто називають дифузійним процесом.
Покажемо, що вінерівський процес є марківським. По теоремі множення ймовірностей тривимірну щільність завжди можна представити у вигляді
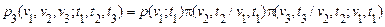 .
.
Нехай  , тоді з (62) маємо
, тоді з (62) маємо
 .
.
Видно, що при фіксованому 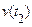 значення
значення  не залежить від
не залежить від  і
і
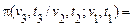
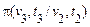 .
.
Тому
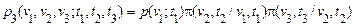 .
.
Шляхом таких же міркувань можна переконатися, що для щільностей ймовірності вищих порядків виконується аналогічне співвідношення, що виражає визначальну властивість марківського процесу.
НА НАСТУПНОМУ ПРАКТИЧНОМУ ЗАНЯТТІ МКР № 1.
| <== попередня сторінка | | | наступна сторінка ==> |
| Білий шум і його моделі | | | Ортогональні проекції точки |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |