
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Прискорення
Прискорення— це кінематична міра зміни вектора швидкості точки. Прискорення — величина векторна. У прямолінійному русі точки вектор швидкості завжди збігається з траєкторією і тому вектор зміни швидкості також збігається з траєкторією. З курсу фізики відомо, що прискорення — це зміна швидкості за одиницю часу. Якщо за невеликий проміжок часу 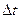 швидкість точки змінилася на
швидкість точки змінилася на 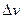 , то середнє прискорення
, то середнє прискорення
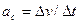
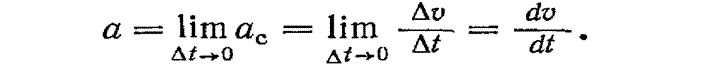 |
Середнє прискорення не дає уявлення про дійсне прискорення у кожний даний момент часу (дійсне прискорення називають миттєвим). Чим менший проміжок часу, за який визначають середнє прискорення, тим ближче воно до дійсного. Дійсне прискорення — це границя, до якої прямує середнє прискорення при
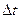 , що прямує до нуля: -
, що прямує до нуля: -
Отже, враховуючи, що  дістаємо
дістаємо 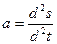
Дійсне прискорення в прямолінійному русі дорівнює першій похідній швидкості за часом або другій похідній координати (відстані від початку відліку переміщення) за часом.
Одиниця прискорення м/с2
Приклад 9.4. Точка рухається прямолінійно за законом s=t4+2t (s- в м,
t — в с). Знайти її середнє прискорення у проміжку між моментами t1 = 5 с, t2= 7 с, а також дійсне значення прискорення в момент 6 с.
Розв’язання. Спочатку визначимо швидкість точки
v=ds/dt=4t3+2
Підставляючи сюди замість і його значення 5 с і = 7 с, знаходимо
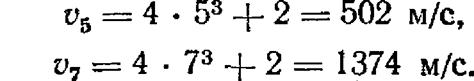 4
4
Отже, приріст швидкості за даний проміжок, часу = 7 — 5 = 2с буде 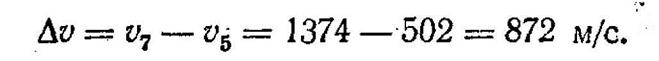 Середнє прискорення точки
Середнє прискорення точки
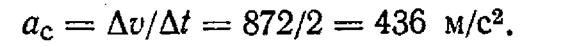
Щоб визначити дійсне прискорення точки, візьмемо похідну від швидкості за часом
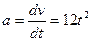

Підставляючи сюди замість і значення t3= 6 с, дістаємо
 42. Найпростіші рухи твердого тіла
42. Найпростіші рухи твердого тіла
Розрізняють два види найпростіших рухів твердого тіла: поступальний і обертальний навколо нерухомої осі.
Рух тіла, під час якого будь-яка пряма, проведена в тілі, залишається паралельною сама собі, називають поступальним. Уявлення про поступальний рух можна скласти, спостерігаючи рух вагона трамвая на прямолінійній ділянці шляху; поступально рухається стіл поздовж ньостругального верстата, поршень стаціонарного двигуна внутрішнього згоряння тощо.
Теорема. У поступальному русі усі точки мають однакові траєкторії, швидкості і прискорення.
Обертання навколо нерухомої осі
Рух, при якому хоча б дві точки твердого тіла чи незмінної системи залишаються нерухомими, називається обертальним; пряма, яка сполучає ці дві точки, називається віссю обертання.В означенні обертального руху йдеться про незмінну систему, тому вісь обертання може бути й за межами тіла.
Обертальний рух у техніці — явище дуже поширене. Переважна більшість механізмів і машин мають ланки, які рухаються обертально, наприклад вали, зубчасті колеса, кривошипи тощо. Зазначимо, що поняття обертального руху може стосуватися лише тіла, але не точки; так, наприклад, рух точки по колу — не обертальний рух, а криволінійний.
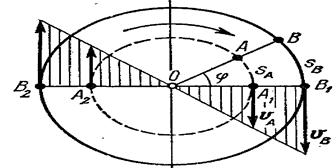
Розглянемо диск, який обертається навколо осі, перпендикулярної до рисунка 10.3.
Точка О — слід цієї осі. Очевидно, що траєкторії точок обертового тіла є кола різних радіусів, розміщені в площинах, перпендикулярних до осі обертання, з центрами, що лежать на пій осі. Рис. Ю.З
Нехай за час t диск повернувся на кут ф. При цьому точка А пройшла шлях sa, а точка В — шлях sв. Оскільки точки, що містяться на різних відстанях від осі обертання, за той самий проміжок часу проходять різні шляхи, то вони мають різні швидкості і прискорення.
Отже, під час обертального руху тіла його точки, що містяться на різних відстанях від осі обертання, мають неоднакові траєкторії, швидкості і прискорення.
Звідси виходить, що лінійне переміщення (шлях), лінійна швидкість і прискорення не можуть характеризувати обертальний рух тіла в цілому. Обертальний рух тіла можна характеризувати кутом ф, на який воно повертається за даний проміжок часу. Цей кут називають кутовим переміщенням тіла. Кутове переміщення виражають у радіанах (рад) або обертах (об); в останньому випадку кутове переміщення позначають N. Щоб установити залежність між кутом ф і Nf складемо пропорцію:
1 об — 2я рад,
N об — ф рад,
звідки
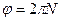 рад,
рад,
де N — кількість обертів тіла.
Кутове переміщення тіла є функцією часу, тому закон обертального руху в загальному вигляді можна записати так:
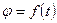
З рис. 10.3 видно, що шлях будь-якої точки обертового тіла
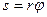
де г — відстань точки від осі обертання.
Швидкість будь-якої точки тіла визначається так:
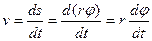
(r винесли за знак похідної, бо для даної точки твердого тіла ця величина
стала). Вираз 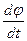 позначимо w і назвемо кутовою швидкістю.
позначимо w і назвемо кутовою швидкістю.
Кутова швидкість — це кінематична міра руху обертового тіла, яка характеризує бистроту його кутового переміщення:
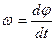
Кутова швидкість дорівнює першій похідній кутового переміщення за часом. Одиниця кутової швидкості рад/с
Формулу для визначення швидкості будь-якої точки обертового тіла записують так:
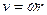
Швидкість точки в кожний момент часу прямо пропорційна її відстані від осі обертання, тому графік швидкостей точок, наприклад діаметра В1В2, матиме вигляд двох трикутників (рис. 10.3). Очевидно, що вектор швидкості точки обертового тіла напрямлений перпендикулярно до радіуса, що з'єднує цю точку з віссю обертання. Якщо точка лежить на по- верхні обертового тіла, то її швидкість називають коловою.
У техніці швидкість обертання часто вимірюють в обертах за хвилину, позначають літерою п і називають частотою обертання. Встановимо залежність між кутовою швидкістю і частотою обертання, вираженими відповідно в рад/с і хвН. Запишемо пропорцію:
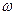 рад — 1 с,
рад — 1 с,
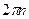 рад — 60 с.
рад — 60 с.
З пропорції знайдемо
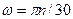 рад/с,
рад/с,
де п — частота обертання тіла, об/хв або хв—1.
| <== попередня сторінка | | | наступна сторінка ==> |
| Швидкість | | | Text 2. Deutsche Feste |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |