• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вектори кутової швидкості і кутового прискорення.

Раніше було з’ясовано, що елементарне кутове зміщення 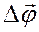можна розглядати як векторну величину.

Вектор елементарного кутового зміщення 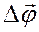є напрямлений відрізок, що чисельно дорівнює куту повороту, напрямлений по осі обертання в сторону, яка вказуються правилом правого гвинта. Як відомо, за цим правилом напрям вектора повинен збігатись з поступальним рухом гвинта, якщо його, ручку повертати за напрямом обертання.

Таким чином, кутова швидкість і кутове прискорення – вектори, напрямлені по осі обертання.

Кутова швидкість – векторна фізична величина, що характеризує бистроту і напрям обертання.

Кутова швидкість – вектор, напрямлений вздовж осі обертання таким чином, щоб з його кінця було видно обертання, що здійснюється проти годинникової стрілки (правило правого гвинта).

Кутове прискорення – це вектор, що збігається з напрямом кутової швидкості в прискорених рухах, або напрямлений проти кутової швидкості в сповільнених рухах.

,

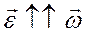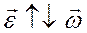
На відміну від розглянутих векторів 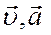, напрями, яких очевидні, вважаються істинними векторами; вектори 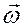і 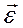називаються псевдовекторами.

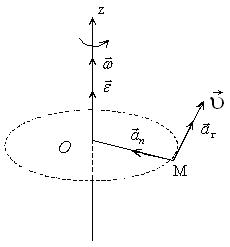
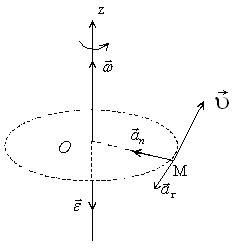
Прискорене обертання	Сповільнене обертання
Рис. 2.3.

Читайте також:

1. Бистрість – це здатність людини до термінового реагування на подразники та до високої швидкості рухів, що виконуються при відсутності значного зовнішнього опору.
2. Білково-експресуючі вектори
3. Вектор кутового зміщення .
4. Вектори зовнішньої політики США
5. Вектори рівні, якщо вони колінеарні, мають однакові напрями і рівні модулі.
6. Вектори, лінійні операції над векторами
7. Вибір маси та швидкості руху пасажирських поїздів.
8. Визначеннч швидкості осадження частинок пі дією сили тяжіння
9. Визначення градієнту зміни швидкості.
10. Визначення швидкості осадження
11. Визначення швидкості початку псевдозрідження

Переглядів: 6667