Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Точки розриву функції

Означення 3.42. Точка 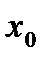така, що функція 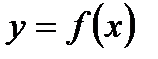, визначена в деякому околі цієї точки, крім, можливо, самої точки 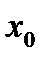, називається точкою розриву, якщо не виконується означення неперервності: .

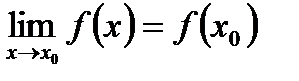Зауважимо, що означення передбачає, що точка 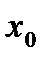є граничною точкою області визначення функції.

Залежно від того, як саме не виконується дана умова, розрізняють декілька типів точок розриву.

Якщо границя функції існує, але не дорівнює значенню функції в точці: , або значення функції в точці не існує, то така точка називається точкою усувного розриву.

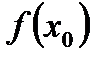
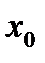
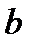
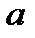
Назва пов’язана з тим, що довизначивши функцію значенням границі, 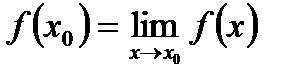, ми досягнемо неперервності.

Якщо границя функції не існує, то точка називається точкою неусувного розриву.

Можливі три варіанти поведінки функції в околі точки, при яких границя не існує.

Існують односторонні границі, але вони не рівні між собою: 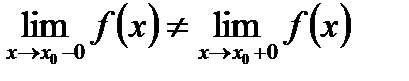. Така точка називається точкою неусувного розриву першого роду (стрибок).

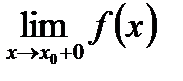
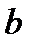
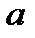
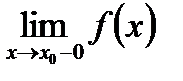
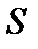
Одна або обидві односторонні границі не існують тому, що функція при 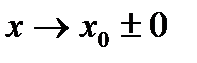є нескінченно великою. Така точка називається точкою неусувного розриву другого роду.

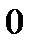
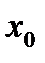
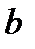
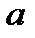
Крім того, неусувний розривбуде у випадку, коли одна або обидві односторонні границі не існують, при тому, що функція є обмеженою у деякому околі точки .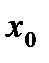

(У нашому курсі ми не будемо розглядати цей тип точок розриву).

Розглянемо приклад.

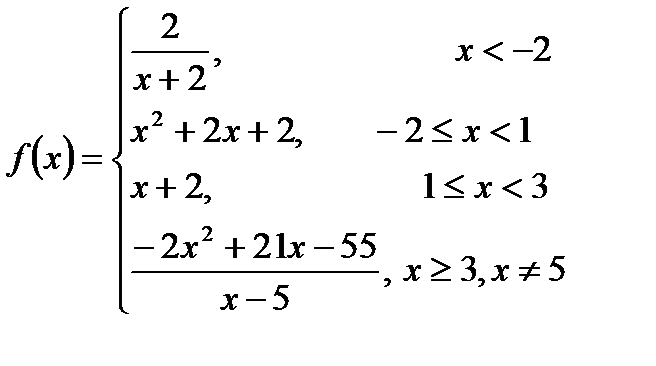Область визначення: 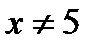. Дана функція не є елементарною, оскільки задається різними аналітичними виразами, кожний із яких визначає елементарну функцію, отже, на кожному з інтервалів функція неперервна. Точка 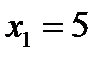- гранична точка області визначення, функція в ній невизначена, 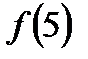не існує, отже, 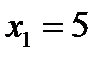- точка розриву. Крім того, функція може мати розриви в точках «стику» різних аналітичних виразів: 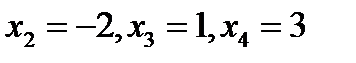. Для встановлення, чи це точки розриву і, можливо, їх класифікації дослідимо границі функцій у цих точках.

1. Точка 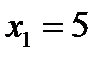. Знайдемо границю :

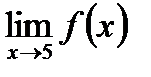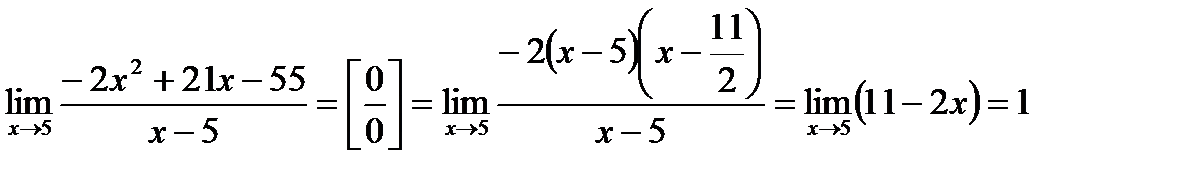Границя існує, отже, це точка усувного розриву і, якщо довизначити 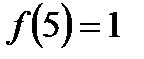, то в цій точці функція буде неперервною.

2. Точка 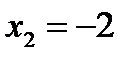. Значення функції в цій точці існує: 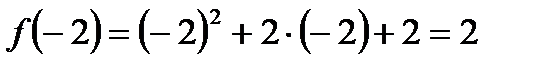. Знайдемо границю 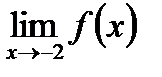. Зліва та справа від цієї точки функція задається різними аналітичними виразами, отже, нам необхідно розглянути односторонні границі. 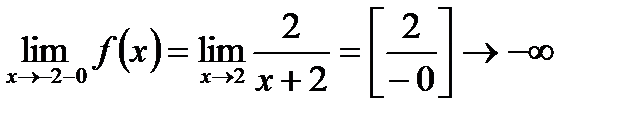, тобто границя не існує, функція є нескінченно великою. Незважаючи на існування чи не існування правосторонньої границі, точка 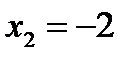є точкою неусувного розриву другого роду. Для побудови ж графіка функції знайдемо правосторонню границю:

3. Точка 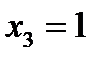. Значення функції в цій точці існує: 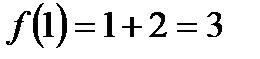. Тут також треба шукати односторонні границі.

. .

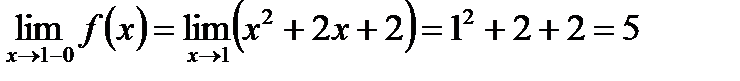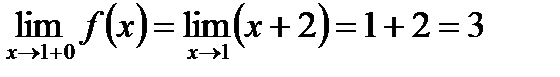Обидві границі існують, але не є рівними, отже, це точка неусувного розриву першого роду – «стрибок».

3. Точка 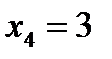. Знайдемо односторонні границі: 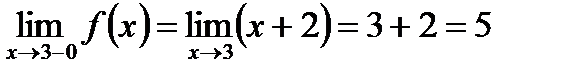. . 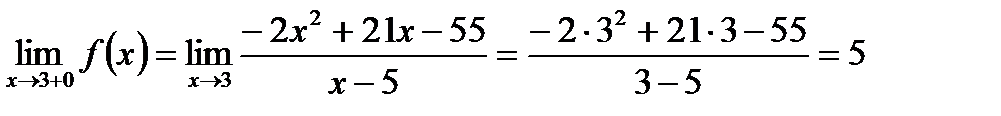Односторонні границі існують і є рівними, отже, існує границя: 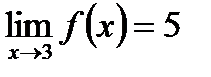. Значення функції в цій точці: 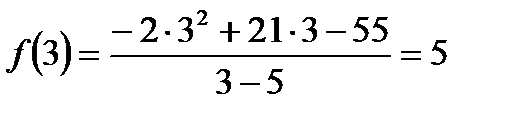дорівнює границі, отже, функція є неперервною.

Зробимо ескіз графіка.

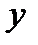
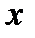
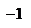
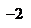
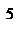
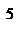
Приклад. Дослідити неперервність функції

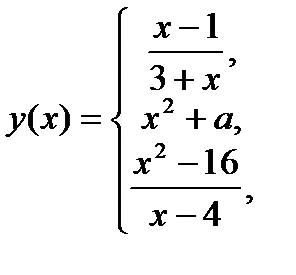
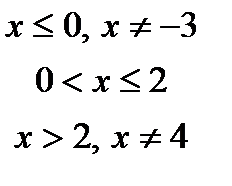та визначити, при якому значенні параметра а функція неперервна в точці .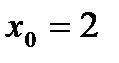

Область визначення: 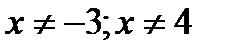. Функція не є елементарною, тому що задана трьома аналітичними виразами. У кожному з трьох проміжків функція є елементарною, отже, на кожному з інтервалів функція є неперервною. У першому проміжку: 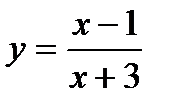. Це дробово-раціональна функція, яка визначена всюди, крім точки .

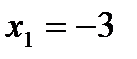У другому проміжку функція має вигляд: 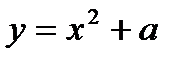. Це поліном, квадратична функція, яка визначена на всій області визначення, тому вона неперервна.

У третьому проміжку: 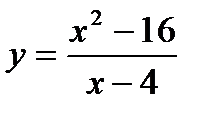. Це дробово-раціональна функція, яка визначена всюди, крім точки .

Крім цих точок, точками розриву можуть бути точки «стику» функцій: .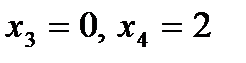

Розглянемо точку 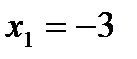. Оскільки вона є граничною точкою області визначення, і 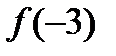не існує, то це точка розриву. Для класифікації даної точки розриву спробуємо знайти границю функції при 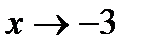: 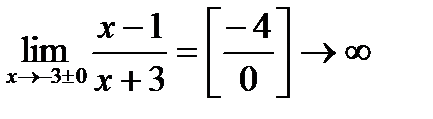. Таким чином, при 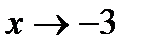функція є нескінченно великою, отже, 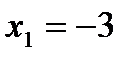точка неусувного розриву другого роду. Для побудови графіка розглянемо односторонні границі:

Лівостороння: 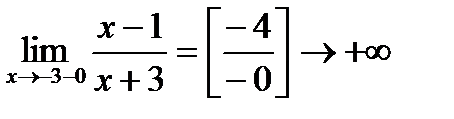, а правостороння: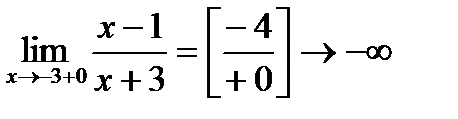

Точка 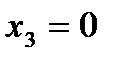. Знайдемо значення функції в точці: .

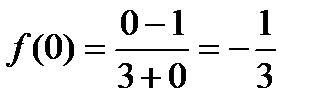Зліва та справа від цієї точки функція задається різними аналітичними виразами, отже, нам необхідно розглянути односторонні границі.

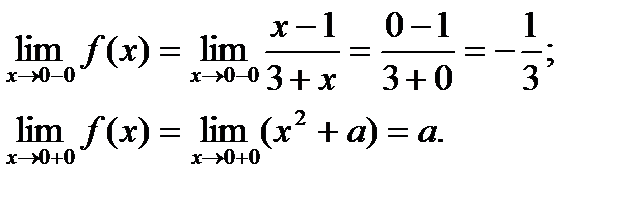
Для того, щоб функція була неперервною в цій точці, необхідно, щоб односторонні границі були рівними, отже, повинна виконуватися рівність: , і в такому випадку границя буде рівною значенню функції в точці. При 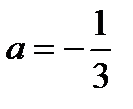функція неперервна в точці .

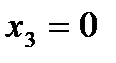Точка 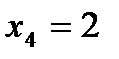. Знайдемо значення функції в цій точці: .

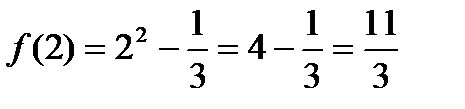Знайдемо односторонні границі:

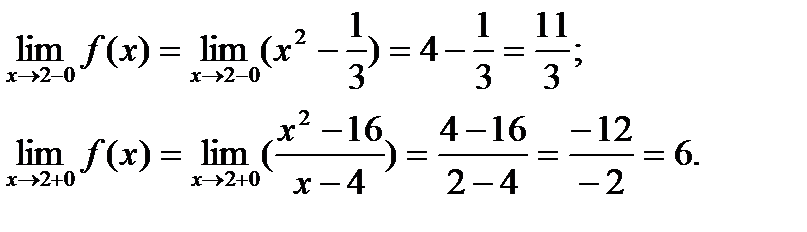
Оскільки обидві границі існують, але не є рівними, то це точка неусувного розриву першого роду – “стрибок”.

Точка 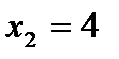. Значення функції в цій точці не існує. Знайдемо границю функції в цій точці:

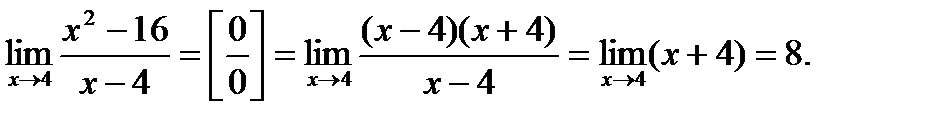
Границя існує, отже, це точка усувного розриву. Якщо довизначати 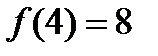, то в цій точці функція буде неперервною.

Зробимо ескіз графіка:

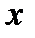
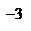
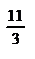
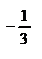
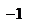
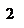
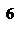
Запитання та завдання для самоперевірки

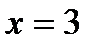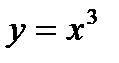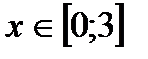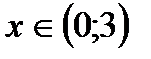1. Чи є точка точкою розриву функції , якщо вона визначена при: а) , б) , в) ?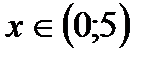

2. Чи є точка 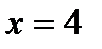точкою розриву функції: 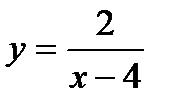, якщо вона визначена при: а) 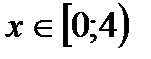, б) ?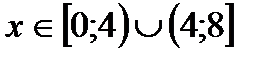

3. При якому значенні параметра 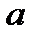функція:

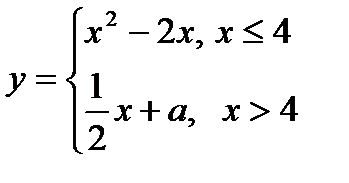
буде неперервною?

4. Дослідіть неперервніть та класифікуйте точки розриву функції:

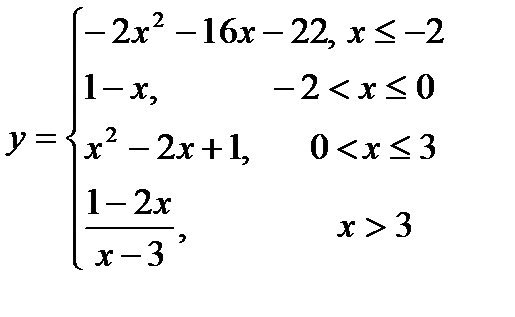
<== попередня сторінка	\|	наступна сторінка ==>
Розкриття невизначеностей	\|	Диференціальне числення

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.