Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розділ 8.2. Диференціальна функція розподілу та її властивості

Нехай випадкова величина 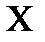– неперервна, тоді функція розподілу F(x) теж неперервна. Нехай в околі точки хфункціяF(x) є диференційованою.

Означення: Диференціальною функцією розподілу f(x) називають першу похідну інтегральної функції F(x), тобто

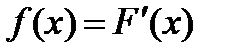. (8.5)

Властивість 1:Диференціальна функція є невід’ємною

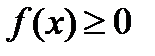Доведення

Ця властивість випливає із означення диференціальної функції як похідної від неспадної функції розподілу F(x). Геометрично це означає, що графік диференціальної функції розміщений або над віссю абсцис, або збігається з нею. Графік диференціальної функції називається кривою розподілу.

Властивість 2: Ймовірність того, що неперервна випадкова величина прийме значення з інтервалу 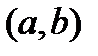дорівнює визначеному інтегралу від диференціальної функції, взятому в межах від а до b, тобто

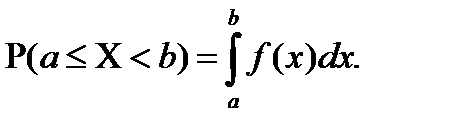(8.6)

Із наслідку 2 розділу 8.1 маємо

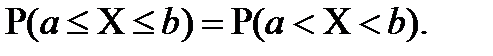
Якщо покласти у формулі (8.6) 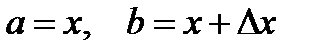і застосувати теорему про середнє значення у визначному інтегралі, то її можна представити

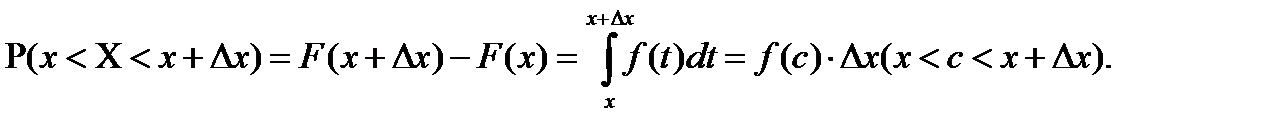
Розділивши обидві частини в останній рівності на 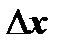, отримаємо

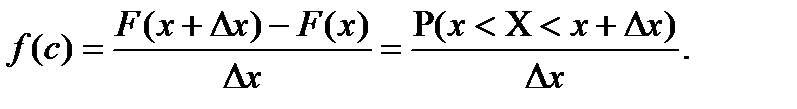
Останнє відношення є середньою щільністю розподілу ймовірностей на проміжку 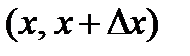. Якщо перейти до границі при 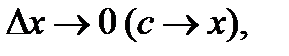то отримаємо

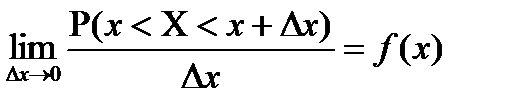. (8.7)

Формула (8.7) задає диференціальну функцію розподілу якщільність розподілу ймовірності неперервної випадкової величини в даній точці. У зв’язку з цим функцію f(x) називають диференціальною функцієюрозподілу або щільністю розподілу.

Приклад:

Дана диференціальна функція випадкової величини. Знайти ймовірність того, що за результатом випробування випадкова величина 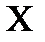прийме значення з інтервалу (0,3 ; 1), якщо диференціальна функція дорівнює

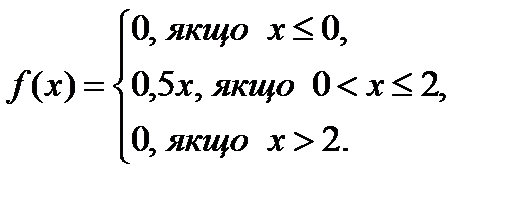
Рішення

За формулою (8.6)

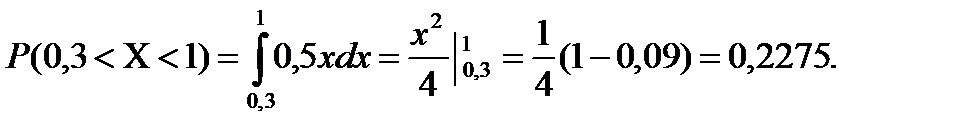
Властивість 3: Інтегральна функція розподілу може бути виражена через диференціальну

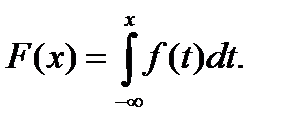(8.8)

Доведення

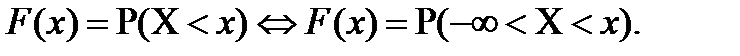
Покладемо у формулі (8.8) 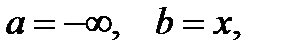маємо

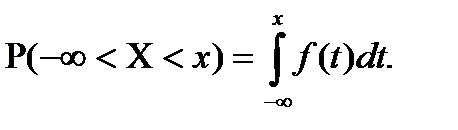
Приклад:

Знайти інтегральну функцію за даною диференціальною функцією

Рішення

Якщо , тоді f(x)=0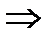F(x)=0. Якщо 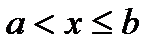, тоді

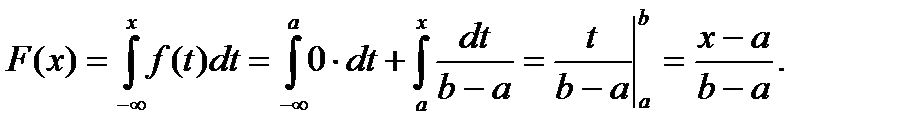
Якщо ж 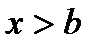, тоді

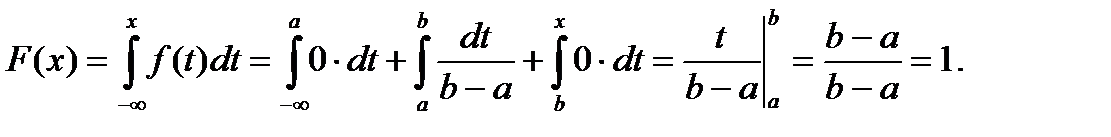
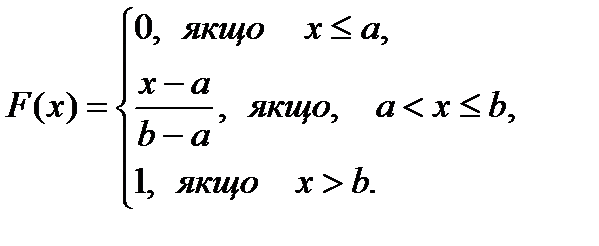
Властивість 4: Інтеграл у нескінченних межах від диференціальної функції дорівнює одиниці

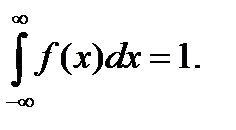(8.9)

Доведення

Цей вираз є ймовірністю події, яка полягає у тому, що випадкова величина прийме значення, яке належить 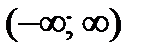, тобто є ймовірністю достовірної події, а ймовірність достовірної події дорівнює одиниці.

Геометрично це означає, що вся площа, обмежена віссю абсцис і кривою щільності розподілу, дорівнює одиниці. У цьому є аналогія щільності розподілу гістограми питомих відносних частот для статистичного ряду.

Приклад:

Диференціальна функція розподілу випадкової величини 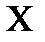задана рівністю 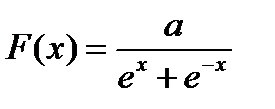, знайти параметр а.

Рішення

За формулою (8.9) одержуємо

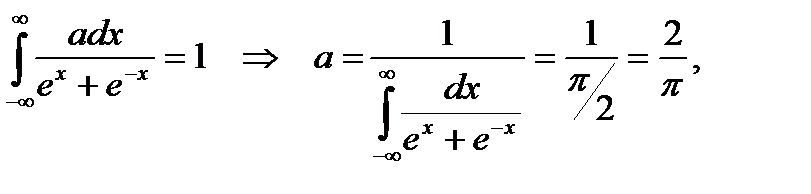
тому що

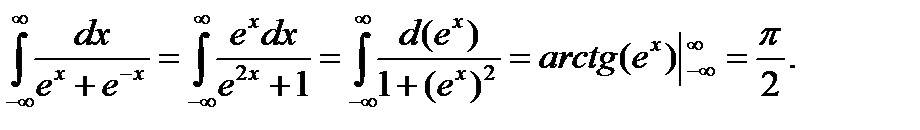
<== попередня сторінка	\|	наступна сторінка ==>
Задачі до розділу 8.1	\|	Задачі до розділу 8.2

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.