
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Формула повної ймовірності.
Бачимо, що ймовірність події можна обчислити як суму або добуток ймовірностей елементарних подій, причому процес встановлення ймовірностей значно спрощується. Саме цій меті служить формула повної ймовірності.
Нехай 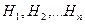 - події, які утворюють повну групу, тобто вичерпують всі можливі випадки даного експерименту. Подія А може відбутися з настанням кожної з подій
- події, які утворюють повну групу, тобто вичерпують всі можливі випадки даного експерименту. Подія А може відбутися з настанням кожної з подій 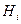 з деякою ймовірністю
з деякою ймовірністю 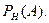
Тоді ймовірність події А обчислюється за формулою
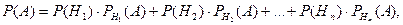
де 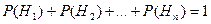 .
.
Події 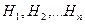 називають гіпотезами.
називають гіпотезами.
Приклад 16. Нехай деталі виготовляють на трьох верстатах. На першому виготовлено 40% всіх деталей, на другому - 35%, і на третьому – 25%. На першому 90% деталей були I сорту, на другому 80%, і на третьому – 70%. Яка ймовірність, що взята деталь I сорту.
Розв’язання: Складемо гіпотези:
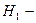 деталь виготовлено на I верстаті,
деталь виготовлено на I верстаті,
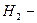 деталь виготовили на II верстаті,
деталь виготовили на II верстаті,
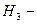 деталь виготовили на III верстаті.
деталь виготовили на III верстаті.
Подія А – взята деталь першого сорту, може відбутися одночасно з кожного з гіпотези 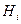 .
.
Тоді
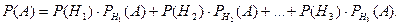
З умови задачі видно, що
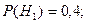
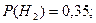
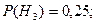
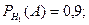
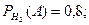

Отже, 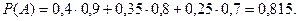
Якщо подія А може настати лише за умови появи однієї з гіпотез 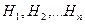 , то ймовірність гіпотез можна переоцінити зо формулою Байєса.
, то ймовірність гіпотез можна переоцінити зо формулою Байєса.
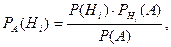
де  ймовірність кожної з гіпотез після випробування, в результаті якого настала подія А;
ймовірність кожної з гіпотез після випробування, в результаті якого настала подія А;
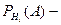 умовна ймовірність події А після настання події
умовна ймовірність події А після настання події 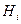 ;
;
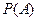 - ймовірність події А, знайдена за формулою повної ймовірності.
- ймовірність події А, знайдена за формулою повної ймовірності.
Приклад 17. В першому ящику 8 білих ; 6 чорних куль, а в другому – 10 білих, 4 чорних. Навмання вибирають і ящик і кулю. Відомо, що вийнята куля чорна. Знайти ймовірність того, що було вибрано перший ящик.
Розв’язання: Введемо позначення: 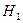 - було вибрано перший ящик;
- було вибрано перший ящик; 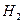 - було вибрано другий ящик; А – при проведенні двох послідовних випробувань вибору ящика і вибору кулі було вийнято чорну кулю.
- було вибрано другий ящик; А – при проведенні двох послідовних випробувань вибору ящика і вибору кулі було вийнято чорну кулю.
Тоді 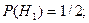
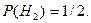 Ймовірність вийняття чорної кулі після того, як вибрано перший ящик, становить
Ймовірність вийняття чорної кулі після того, як вибрано перший ящик, становить 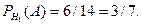 Ймовірність виймання чорної кулі після того, як вибрано другий ящик, дорівнює
Ймовірність виймання чорної кулі після того, як вибрано другий ящик, дорівнює 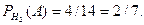 За формулою повної ймовірності того, що вийнята куля була чорною
За формулою повної ймовірності того, що вийнята куля була чорною
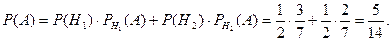
Ймовірність того, що чорну кулю було вийнято з першого ящика, обчислюємо за формулою Байєса
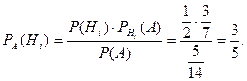
Формула Бернуллі.
Нехай відбудеться n незалежних випробувань, в кожному з яких ймовірність того, що відбудеться подія А рівна р. Тоді ймовірність того, що при n випробуваннях подія А відбудеться рівно k разів обчислюється за формулою Бернуллі.
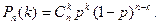
Дійсно, випадок, коли подія А відбудеться в кожному з перших k випробувань, і не відбудеться в інших n- k випробувань можна представити як добуток подій А і 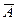 :
:
 .
.
Згідно умови, всі випробування незалежні, тому
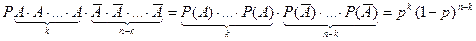
Подія А може відбутись k раз при п випробувань і в іншій послідовності, наприклад
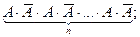
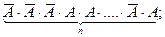
Але ймовірність залишається незмінною, бо від перестановки множників, бо від перестановки множників добуток не змінюється. Число всіх можливих послідовностей, в яких відбуватимуться події А і 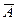 рівне
рівне 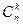 . Додавши всі можливі випадки, по теоремі додавання ймовірностей несумісних подій отримуємо формулу Бернуллі.
. Додавши всі можливі випадки, по теоремі додавання ймовірностей несумісних подій отримуємо формулу Бернуллі.
Приклад 18. Ймовірність влучення в ціль з одного пострілу 0,8. Яка ймовірність влучити в ціль 7 разів з 10 пострілів?
Розв’язання: Загальне число випробувань п=10; число влучень k=7. Отже, ймовірність влучити 7 разів з 10 пострілів згідно формули Бернуллі рівна:

Приклад 19. В урні 20 куль: 15 білих і 5 чорних. З урни послідовно беруть 5 куль, причому кожну взяту кулю повертають в урну перед наступною спробою. Знайти ймовірність того, що з 5 куль 2 будуть білі.
Розв’язання: Ймовірність взяти білу кулю в кожній спробі рівна 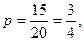 а чорну -
а чорну - 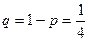 . По формулі Бернуллі знайдемо:
. По формулі Бернуллі знайдемо:
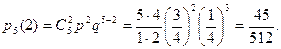
Дискретна випадкова величина, та її основні характеристики.
Випадковою величиною називають змінну Х, яка в результаті випробування може прийняти одне й лише одне значення, не відоме раніше і таке, що залежить від наслідку випробування. Можна пояснити, що величина буде випадковою, якщо вона приймає в даному випробуванні різні значення.
Випадкові величини поділяються на дискретні та неперервні. Ми розглядатимемо дискретні випадкові величини.
Величину Х називаємо дискретною випадковою величиною, якщо множина її можливих значень є скінченою або нескінченою послідовністю чисел 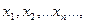 де кожне співвідношення
де кожне співвідношення 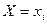 є елементарною випадковою подією і має визначену ймовірність
є елементарною випадковою подією і має визначену ймовірність 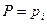 .
.
Оскільки, кожне значення дискретної випадкової величини має визначену ймовірність, то дані спостережень зручно заносити у таблицю:
табл.1
| Значення випадкової величини Х | 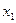
| 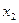
| …. | 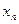
|
| Ймовірність цього значення Р | 
| 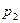
| …. | 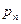
|
Дана таблиця носить назву таблиці закону розподілу дискретноївипадкової величини. Закони розподілу можна задати також у вигляді рівняння або графічно.
Отже, законом розподілу дискретної випадкової величини Х називають співвідношення між можливим значенням 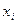 та їх ймовірністю
та їх ймовірністю 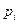 .
.
Якщо випадкова величина Х може набувати скінчене число різних значень 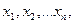 то елементарні події
то елементарні події 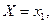
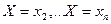 утворюють повну групу і тому сума їх ймовірностей дорівнює одиниці, тобто
утворюють повну групу і тому сума їх ймовірностей дорівнює одиниці, тобто
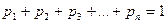 .
.
Важливою характеристикою дискретної випадкової величини Х є математичне очікування.
Математичне очікування 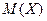 дискретної випадкової величини Х називають суму добутків всіх її можливих значень
дискретної випадкової величини Х називають суму добутків всіх її можливих значень 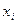 на їх ймовірність
на їх ймовірність 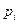 :
:
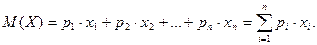
Властивості математичного очікування.
- Математичне очікування постійної величини дорівнює самій постійній
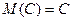
- Математичне очікування суми випадкових величин дорівнює сумі математичних очікувань доданків:
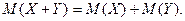
- Математичне очікування добутку незалежних випадкових подій дорівнює добутку математичних очікувань цих величин:
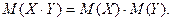
- постійний множник можна виносити за знак математичного очікування:
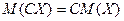 .
.
Приклад: Знайти математичне очікування величини X і Y, якщо відомі закони їх розподілу
| Х | -8 | -4 | -1 | |||
| Р | 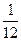
| 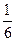
| 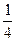
| 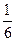
| 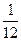
|  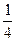
|
| Y | -2 | -1 | ||||
| Р | 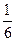
| 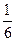
| 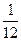
| 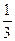
|  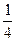
|
Розв’язання: Знайдемо математичні очікування:
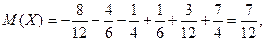
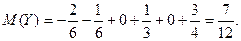
Ми отримали цікавий результат: закони розподілу величини X і Y різні, а їх математичні очікування однакові.
З рисунку 1 видно, що значення величини Y зосереджено біля математичного очікування М(Y) (рис.1б), а значення
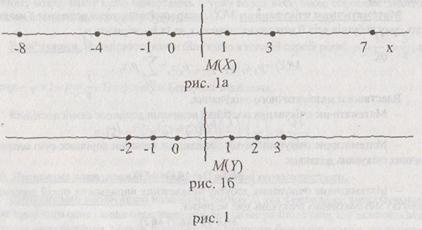
Величини Х розкидано (розсіяно) далі від математичного очікування М(Х) (рис.1а).
Основною числовою характеристикою розсіяння можливих значень, випадкової величини Х є дисперсія D(X), яка визначається за формулою:
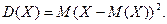
Величину 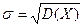 називають середнім квадратичним відхиленням випадкової величини Х.
називають середнім квадратичним відхиленням випадкової величини Х.
Властивості дисперсії:
- Дисперсія постійної величини, очевидно, дорівнює нулю: DC=0.
- Сталий множник можна виносити за знак дисперсії, піднявши його до квадрату:
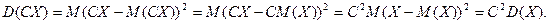
- Дисперсія дорівнює математичному очікуванню квадрата випадкової величини мінус квадрат її математичного очікування:
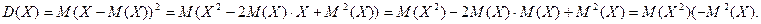
- Якщо до всіх значень випадкової величини додати (відняти постійне число, то дисперсія її не зміниться:
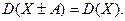
Приклад 20. Дискретна випадкова величина розділена за законом:
| Х | -1 | |||
| Р | 0,2 | 0,1 | 0,3 | 0,4 |
Знайти D(X).
Розв’язання: Спочатку знайдемо:
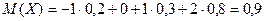
а далі
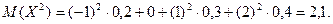
Знайдемо дисперсію:
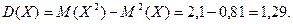
| <== попередня сторінка | | | наступна сторінка ==> |
| Теорема множення ймовірностей залежних подій. | | | Закон великих чисел. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |