• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Незалежні події. Теорема множення для незалежних подій

Нехай ймовірність події В не залежить від появи події А.

Подію В називають незалежною від події А, якщо поява події А не змінює ймовірності події В, тобто якщо умовна ймовірність події В дорівнює її безумовній ймовірності:

. (*)

Підставивши (*) у співвідношення (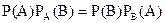) попереднього параграфа, одержимо

.

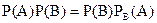Звідси

,

тобто умовна ймовірність події А в припущенні, що наступила подія В, дорівнює її безумовній ймовірності. Іншими словами, подія А не залежить від події В.

Отже, якщо подія В не залежить від події А, то і подія А не залежить від події В. Це означає, що властивість незалежності подій взаємна.

Для незалежних подій теорема множення 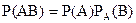має вид

, (**)

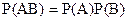тобто ймовірність спільної появи двох незалежних подій дорівнює добутку ймовірностей цих подій.

Рівність (**) приймають як визначення незалежних подій.

Дві події називають незалежними, якщо ймовірність їхнього суміщення дорівнює добутку ймовірностей цих подій; у протилежному випадку події називають залежними.

На практиці висновок про незалежність подій роблять за змістом задачі. Наприклад, ймовірності поразки цілі кожною із двох гармат не залежать від того, чи вразила ціль інша гармата, тому події "перша гармата вразила ціль" і "друга гармата вразила ціль" незалежні.

Приклад 1. Знайти ймовірність спільного враження цілі двома гарматами, якщо ймовірність поразки цілі першою гарматою (подія А) дорівнює 0,8, а другою (подія В) - 0,7.

Розв’язок. Події А і В незалежні, тому, за теоремою множення, шукана ймовірність

.

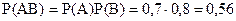Зауваження. 1. Якщо події А і В незалежні, то незалежні також под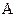ії і 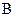, і , і .

Кілька подій називають попарно незалежними, якщо кожні дві з них незалежні. Наприклад, події А, В, С попарно незалежні, якщо незалежні події А і В, А і С, В і С.

Для того щоб узагальнити теорему множення на декілька подій, уведемо поняття незалежності подій у сукупності.

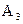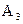Декілька подій називають незалежними у сукупності (чи просто незалежними), якщо незалежні кожні дві з них і незалежна кожна подія і всі можливі добутки останніх. Наприклад, якщо події , , незалежні в сукупності, то незалежні події 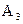і , і 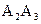, і ; і ,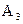і , і . Зі сказаного випливає, що якщо події незалежні в сукупності, то умовна ймовірність появи будь-якої події з них, обчислена у припущенні, що наступили будь-які інші події з числа останніх, дорівнює її безумовній ймовірності.

Підкреслимо, що якщо кілька подій незалежні попарно, то звідси ще не випливає їхня незалежність у сукупності. У цьому розумінні вимога незалежності подій у сукупності сильніша вимоги їхньої попарної незалежності.

Пояснимо сказане на прикладі. Нехай в урні знаходиться 4 кулі, пофарбовані: одна - у червоний колір (А), одна - у синій колір (В), одна - у чорний колір (С) і одна - в усі ці три кольори (ABC). Чому дорівнює ймовірність що витягнута з урни куля має червоний колір?

Так як з чотирьох куль дві мають червоний колір, то Р(А)=2/4=1/2. Міркуючи аналогічно, знайдемо Р(В)=1/2, Р(С)=1/2. Припустимо тепер, що узята куля має синій колір, тобто подія В вже відбулася. Чи зміниться ймовірність того, що витягнута куля має червоний колір, тобто чи зміниться ймовірність події А? Із двох куль, що мають синій колір, одна куля має і червоний колір, тому ймовірність події А, як і раніше дорівнює 1/2. Іншими словами, умовна ймовірність події А, обчислена в припущенні, що наступила подія В, дорівнює її безумовній ймовірності. Отже, події А і В незалежні. Аналогічно прийдемо до висновку, що події А і С, В і С незалежні. Отже події А, В і С попарно незалежні.

Чи незалежні ці події в сукупності? Виявляється, ні. Дійсно, нехай витягнута куля має два кольори, наприклад, синій і чорний. Чому дорівнює ймовірність того, що ця куля має і червоний колір? Лише одна куля пофарбована в усі три кольори, тому взята куля має і червоний колір. Таким чином, припустивши, що події В і С відбулися, дійдемо висновку подія А обов’язково наступить. Отже, ця подія достовірна й ймовірність її дорівнює одиниці. Іншими словами, умовна ймовірність події 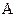не дорівнює її безумовній ймовірності 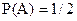. Отже, попарно незалежні події А, В, С не є незалежними в сукупності.

Приведемо тепер наслідок з теореми множення.

Наслідок. Ймовірність спільної появи декількох подій, незалежних у сукупності, дорівнює добутку ймовірностей цих подій:

.

Доведення. Розглянемо три події: А, В і С. Поєднання подій А, В і С рівносильне поєднанню подій АВ і С, тому

.

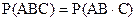Оскільки події А, В і С незалежні в сукупності, то незалежні, зокрема, події АВ і С, а також А і В. За теоремою множення для двох незалежних подій маємо:

i .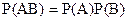

Отже, остаточно одержимо

.

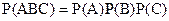Зауваження. Якщо події 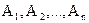незалежні в сукупності, то і протилежні їм події також незалежні в сукупності.

Приклад 2. Знайти ймовірність спільної появи герба при одному киданні двох монет.

Рішення. Ймовірність появи герба першої монети (подія А)

.

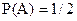Ймовірність появи герба другої монети (подія В)

.

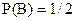Події А и В незалежні, тому шукана ймовірність за теоремою множення дорівнює

.

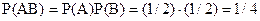Приклад 3. У кожному з 3 ящиків знаходиться по 10 деталей. У першому ящику 8, у другому 7 і в третьому 9 стандартних деталей. З кожного ящика навмання виймають по одній деталі. Знайти ймовірність того, що всі три вийняті деталі виявляться стандартними.

Розв’язок. Ймовірність того, що з першого ящика вийнята стандартна деталь (подія А),

.

Ймовірність того, що з другого ящика вийнята стандартна деталь (подія В),

.

Ймовірність того, що з третього ящика вийнята стандартна деталь (подія С),

.

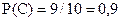Тому що події А, В і С незалежні в сукупності, то шукана ймовірність (за теоремою множення) дорівнює

.

Наведемо приклад спільного застосування теорем додавання і множення.

Приклад 4. Ймовірності появи кожної з трьох незалежних подій , , 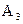відповідно рівні , , 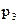. Знайти ймовірність появи тільки одної з цих подій.

Розв’язок. Відмітимо, що, наприклад, поява тільки першої події рівносильна появі події , (з’явилася перша і не з’явилися друга і третя події). Введемо позначення:

- з’явилася тільки подія , тобто ;

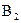- з’явилося тільки подія , тобто ;

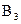- з’явилася тільки подія 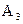, тобто .

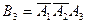Таким чином, щоб знайти ймовірність появи тільки однієї з подій , , , 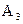будемо шукати ймовірність появи одної, байдуже якої з подій , , .

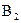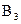Так як події , , 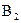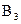несумісні, то застосовна теорема додавання

. (*)

Залишається знайти ймовірності кожної з подій , , .

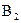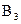Події незалежні, отже, незалежні події , , , тому до них застосовна теорема множення

.

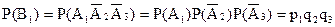Аналогічно,

;

.

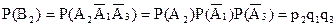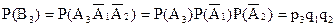Підставивши ці ймовірності в (*), знайдемо шукану ймовірність появи тільки однієї з подій :

.

Читайте також:

1. Аксіоми додавання і множення
2. Алгебра випадкових подій
3. Алгебра подій
4. Безвілля, його заподій і переборення.
5. Безстатеве розмноження та його біологічне значення
6. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
7. Боротьба за возз’єднання Української держави, за незалежність у 60- 80-х роках XVII ст.
8. Боротьба за возз’єднання Української держави, за незалежність у 60-80-х роках XVII ст.
9. В. Друга теорема про розклад.
10. Види випадкових подій
11. Визначення базисних подій. Ідентифікація ризику.
12. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).

Переглядів: 7081