Біноміальний розподіл

Закон розподілу ймовірностей дискретної випадкової величини

На перший погляд може здатися, що для завдання дискретної випадкової величини достатньо перерахувати всі її можливі значення. Насправді це не так: випадкові величини можуть мати однакові переліки можливих значень, а ймовірності їх - різні. Тому для завдання дискретної випадкової величини недостатньо перерахувати всі можливі її значения, потрібно ще указати їх ймовірності.

Законом розподілу дискретної випадкової величини називають відповідність між можливими значеннями і їх ймовірностями; його можна задати таблично, аналітично (у вигляді формули) і графічно.

При табличному завданні закону розподілу дискретної випадкової величини перший рядок таблиці утримує можливі значення, а другий - їх ймовірності:

X	x₁	x₂	…	x_n
p	p₁	p₂	…	p_n

Взявши до уваги, що в одному випробуванні випадкова величина приймає одне і лише одне можливе значення, робимо висновок, що події Х=х₁, Х=х₂, ..., X=х_n, утворюють повну групу; отже, сума ймовірностей цих подій, тобто сума ймовірностей другого рядка таблиці, дорівнює одиниці:

p₁+p₂+...+p_n=1.

Якщо безліч можливих значень Х нескінченна (рахунково), то ряд p₁+p₂+... сходиться і його сума дорівнює одиниці.

Приклад. В грошовій лотереї випущено 100 квитків. Розігрується один виграш в 50 грн. і десять виграшів по 1 грн. Знайти закон розподілу випадкової величини Х - вартості можливого виграшу для власника одного лотерейного квитка.

Рішення. Напишемо можливі значення Х: х₁=50, х₂=1, х₃=0. Ймовірності цих можливих значень такі: p₁=0,01, р2=0,1, р₃=1-(р₁+р₂)=0,89.

Напишемо шуканий закон розподілу:

Х
р	0,01	0,1	0,89

Контроль: 0,01+0,1+0,89=1.

Для наочності закон розподілу дискретної випадкової величини можна зобразити і графічно, для чого в прямокутній системі координат будують точки (х_і, р_і), а потім з’єднують їх відрізками прямих. Отриману фігуру називають багатокутником розподілу.

• Хай проводиться п незалежних випробувань, в кожному з яких подія А може з’явитися або не з’явитися. Ймовірність настання події у всіх випробуваннях постійна і рівна р (отже, ймовірність непояви q=1-р). Розглянемо в якості дискретної випадкової величини Х число появ події А в цих випробуваннях.

Поставимо перед собою завдання знайти закон розподілу величини Х. Для її рішення потрібно визначити можливі значення Х і їх ймовірності . Очевидно, подія А в n випробуваннях може або не з’явитися, або з’явитися 1 раз, або 2 рази, ..., або n разів. Таким чином, можливі значення Х наступні: х₁=0, х₂=1, х₃=2, ..., _хn+1=n. Залишається знайти ймовірності wих можливих значень, для чого достатньо скористатися формулою Бернуллі:

, (*)

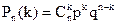де 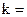0, 1, 2, ..., n.

Формула (*) і є аналітичним вираженням шуканого закону розподілу.

Біноміальним називають розподіл ймовірностей, що визначається формулою Бернуллі. Закон названий біноміальним тому, що праву частину рівності (*) можна розглядати як загальний член розкладання бінома Ньютона:

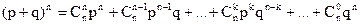Таким чином, перший член розкладання pⁿ визначає ймовірність настання даної події n разів в n незалежних випробуваннях; другий член визначає ймовірність настання події n-1 раз; … ; останній член qⁿ визначає ймовірність того, що подія не з’явиться жодного разу. Напишемо біноміальний закон у вигляді таблиці:

X	n	n-1	…	k	...
P					...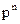

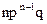
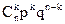
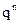
Приклад. Монета кинута 2 рази. Написати у вигляді таблиці закон розподілу випадкової величини Х - числа випадань „герба”.

Рішення. Ймовірність появи „герба» в кожному випробуванні р=1/2, отже, ймовірність непояви „герба”q=1-1/2=1/2.

При двох киданнях монети гербќ може з’явитися або 2 раз, або 1 раз, або зовсім не з’явитися. Таким чином, можливі ачения Х такі: х₁=2, х₂=1, х₃=0. Знайдемо ймовірності цих можливих значень за формулою Бернуллі:

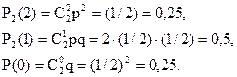
Напишемо шуканий закон розподілу:

Х
р	0,25	0,5	0,25

Контроль: 0,25+0,5+0,25=1.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Дискретні і неперервні випадкові величини	\|	Розподіл Пуассона

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.