
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ЧИСЛОВІ ХАРАКТЕРИСТИКИ ДИСКРЕТНИХ ВИПАДКОВИХ ВЕЛИЧИН
Рис. 1
Графік функції розподілу
Доведені властивості дозволяють представити, як виглядає графік функції розподілу безперервної випадкової величини.
Графік розташований в смузі, обмеженій прямими у=0, у=1 (перша властивість).
При зростанні х в інтервалі (а, b), у якому укладені всі можливі значення випадкової величини, графік підіймається вверх (друга властивість).

При 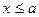 ординати графіка рівні нулю; при
ординати графіка рівні нулю; при  ординати графіка рівні одиниці (третя властивість).
ординати графіка рівні одиниці (третя властивість).
Графік функції розподілу безперервної випадкової величини зображений на рис. 1.
Зауваження. Графік функція розподілу дискретної випадкової величини має ступінчастий вигляд (рис. 2).
Приклад. Дискретна випадкова величина Х задана таблицею розподілу
| X | |||
| p | 0,3 | 0,1 | 0,6 |
Знайти функцію розподілу і накреслити її графік.
Розв’язок. Якщо 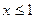 то
то 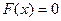 (третя властивість)
(третя властивість)
Якщо 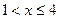 , то
, то  . Дійсно, Х може прийняти значення 1 з ймовірністю 0,3.
. Дійсно, Х може прийняти значення 1 з ймовірністю 0,3.
Якщо 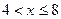 , то
, то 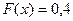 . Дійсно, якщо х задовольняє нерівність
. Дійсно, якщо х задовольняє нерівність 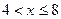 , то
, то 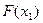 дорівнює ймовірності події
дорівнює ймовірності події 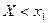 , яка може бути здійснена, коли Х прийме значення 1 (ймовірність цієї події дорівнює 0,3) або значення 4 (ймовірність цієї події дорівнює 0,1). Оскільки ці дві події несумісні, то за теоремою додавання ймовірностей ймовірність події
, яка може бути здійснена, коли Х прийме значення 1 (ймовірність цієї події дорівнює 0,3) або значення 4 (ймовірність цієї події дорівнює 0,1). Оскільки ці дві події несумісні, то за теоремою додавання ймовірностей ймовірність події 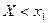 рівна сумі ймовірностей 0,3+0,1=04.
рівна сумі ймовірностей 0,3+0,1=04.
Якщо 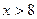 , то
, то . Дійсно, подія
. Дійсно, подія  достовірна, отже, її ймовірність дорівнює одиниці.
достовірна, отже, її ймовірність дорівнює одиниці.
Отже, функція розподілу аналітично може бути записана так:
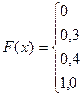
Графік цієї функції наведений на рис. 3.

Рис. 2.
Запитання для самоперевірки:
- Дайте визначення випадкової величини.
- Яку випадкову величину називають дискретною?
- Яку випадкову величину називають неперервною?
- Якими способами можна задати закон розподілу?
- Як називають графічне зображення закону розподілу дискретної випадкової величини?
- Дайте визначення біноміального закону розподілу. Чому його називають біноміальним?
- При яких умовах для задання закону розподілу використовують асимптотичну формулу Пуассона?
- Що називають потоком подій?
- Які властивості притаманні найпростішим потокам подій?
- У чому полягає властивість стаціонарності потоку?
- У чому полягає властивість відсутності післядії?
- У чому полягає властивість ординарності потоку?
- Якою формулою можна описати властивості найпростішого потоку?
- Дайте характеристику геометричного розподілу.
- Дайте визначення і поясніть сутність функції розподілу випадкової величини.
- Наведіть властивості функції розподілу.
- Зобразіть графік функції розподілу.
Як уже відомо, закон розподілу повністю характеризує випадкову величину. Однак часто закон розподілу невідомий і доводиться обмежуватися меншими відомостями. Іноді навіть вигідніше користуватися числами, які описують випадкову величину сумарно; такі числа називають числовими характеристикам випадкової величини. До числа важливих числових характеристик ставиться математичне сподіванння і дисперсія.
Читайте також:
- V. Поняття та ознаки (характеристики) злочинності
- Абсолютна величина числа позначається символом .
- Абсолютні і відносні величини
- Абсолютні і відносні статистичні величини
- Абсолютні, відносні та середні величини.
- Акустичні характеристики порід
- Алгебра випадкових подій
- Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
- Багатовимірні випадкові величини. Система двох випадкових величин
- Будова, принцип роботи та характеристики МДН – транзисторів
- Будова, принцип роботи та характеристики тиристорів
- Будова, характеристики і параметри біполярного транзистора
| <== попередня сторінка | | | наступна сторінка ==> |
| Властивості функції розподілу | | | Математичне сподіванння дискретної випадкової величини |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |