• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Визначити

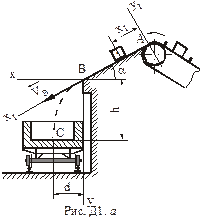
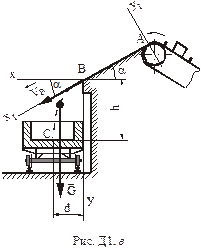
1. Яку швидкість необхідно надати стрічці транспортера, щоб місцем падіння куснів обрізі була середина вагонетки (розмір , рис.Д1.а)?

2. Як залежить дальність польоту шматків від їхньої маси?

3. Яку швидкість здобуває кусень обрізі в момент відриву від лотка ?

Дано:

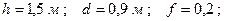
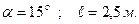
Визначити:

1. - ?

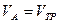2. - ?

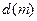3. - ?

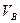Розв'язування.

Для дослідження руху кусень обрізі заміняємо матеріальною точкою масою 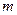. Рух точки від початку лотка 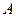до місця падіння умовно розіб'ємо на дві ділянки: прямолінійну - 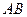і криволінійну - 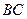. Сили, що діють на точку на кожній з ділянок, постійні за величиною і напрямком.

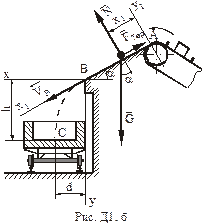
1. Розглянемо рух матеріальної точки на ділянці 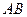. Система координат з початком у точці 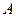показана на рис.Д1.а. Зобразимо точку на ділянці 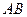в довільний момент часу (рис.Д1.б). Зобразимо сили, що діють на точку в цей момент часу. Цими силами є: вертикальна за напрямком сила ваги 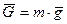; нормальна реакція похилої площини 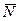і сила тертя ковзання 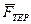, спрямована уздовж площини лотка проти руху.

Запишемо динамічні рівняння руху точки в проекціях на обрані осі координат. Проекції сил, що співпадають з осями за напрямком, вважаємо додатними, а протилежні – від’ємними.

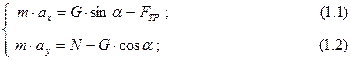
Якщо координата 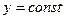, маємо .

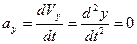Тоді із (1.2) 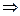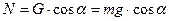, що дозволяє обчислити силу тертя ковзання .

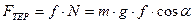Тепер, якщо підставити значення 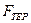в (1.1), отримаємо:

;

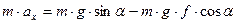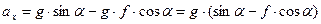
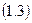
Перетворимо (1.3) в диференціальне рівняння шляхом заміни .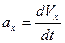

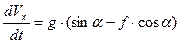
Інтегруючи (1.4) при 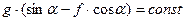будемо мати:

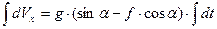
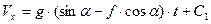
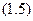
Константу 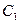визначимо з початкової умови: .

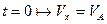Тоді :

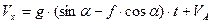
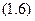
Для моменту часу 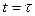маємо 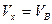, тобто

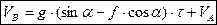
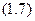
Аналогічно інтегруємо рівняння (1.6), враховуючи, що 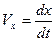, а 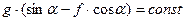. Одержимо:

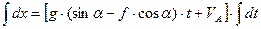
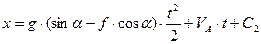
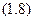
Константу 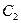визначимо з початкової умови: .

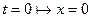Тоді:

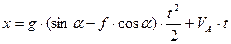
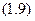
Для моменту часу 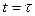маємо 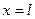, тобто

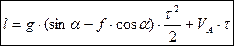
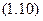
2. Розглянемо рух матеріальної точки на ділянці криволінійного руху 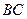. Система координат з початком в точці 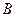показана на рис. Д1.а. Зобразимо точку на ділянці 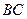в довільний момент часу (рис. Д1.в). Зобразимо сили, що діють на точку в цей момент часу. На точку діє тільки одна сила - вертикальна сила ваги 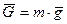(опором повітря нехтуємо). Запишемо динамічні рівняння руху точки в проекціях на осі координат:

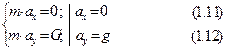
Перетворимо рівняння (1.11) у диференціальне і розв’яжемо його.

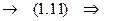
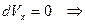
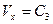
Використовуючи початкову умову 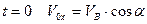, знаходимо .

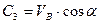Тоді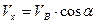

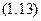
Перетворимо (1.13) у диференціальне рівняння і розв’яжемо його.

.

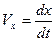
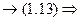
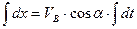
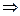
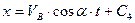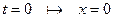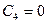З початкової умови: маємо , а

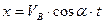
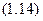
Підставляючи в (1.14) 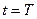, знайдемо координату 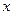точки падіння :

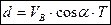
Перетворимо рівняння (1.12) у диференціальне і розв’яжемо його.

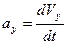
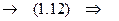
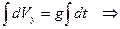
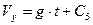
З початкової умови: 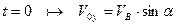маємо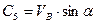

Тоді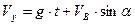

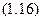
Перетворимо рівняння (1.16) у диференціальне і розв’яжемо його:

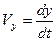
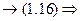
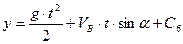
З початкової умови маємо: 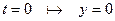. Тому 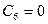, а

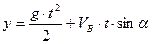
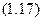
Підставляючи в (1.17) 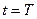, знайдемо координату 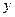точки падіння :

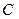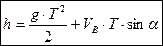
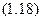
Розглянемо систему рівнянь (1.7), (1.10), (1.15) і (1.18). Чотири рівняння містять чотири невідомих параметри: 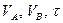і 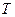, тобто система має розв’язок. Після підстановки відомих величин маємо наступне:

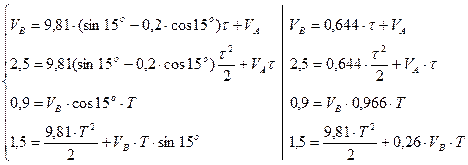
Виконавши обчислення, отримаємо:

; ; ; .

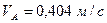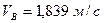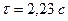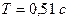Частину із знайдених величин потрібно визначити за умовою задачі.

Аналіз рівняння (1.15) дозволяє відповісти ще на одне з питань умови - дальність польоту точки не залежить від її маси.

Відповідь.

1. Необхідна швидкість стрічки транспортера .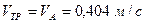

2. Дальність польоту шматків обрізі не залежить від їх маси.

3. Швидкість кусня в момент відриву від лотка .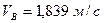

Завдання Д-2. Динамічні рівняння руху тіл

Умова завдання. Механічна система складається з вантажів 1 і 2, циліндричного однорідного котка 3 та ступінчастих шківів 4 і 5 з радіусами ступіней 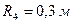, , , 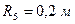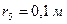(масу кожного шківа вважати розподіленою по зовнішньому ободу) (рис.Д2.0 – Д2.9, табл.Д2). Якщо маса вантажу дорівнює нулю, на рисунку його не зображати. Тіла пов'язані між собою нерозтяжними нитками, намотаними на шківи; ділянки ниток паралельні відповідним площинам.

Система рухається під дією сили 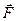. На шківи 4 та 5 діють постійні моменти опору, що дорівнюють відповідно 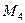та .

Визначити.Силу натягу нитки, що утримує вагомий вантаж.

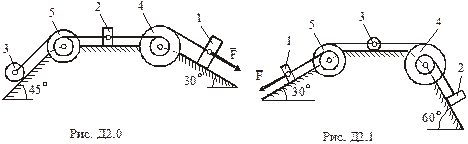
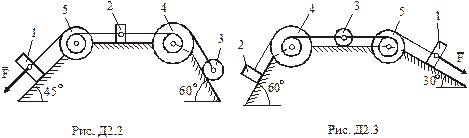
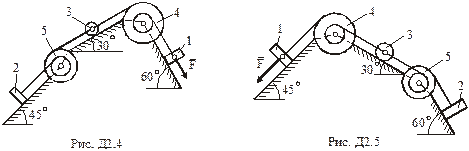
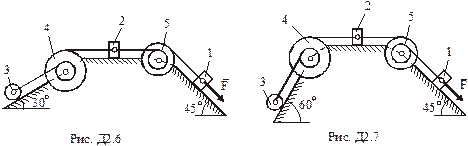
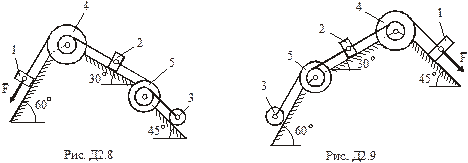
Табл. Д2

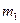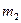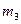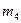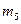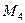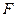№ умови	, кг	, кг	, кг	, кг	, кг	, Н·м	, Н·м	, Н
						0,6 0,3 0,9 0,6 0,3	0,8 0,4 0,6 0,8 0,4

Теоретичне обґрунтування : [5] § 100, 102, 110, 111, 115, 118, 128, 130;

[6] Розд.III. Гл.3. § 2 – 4 , Гл.4. § 2 – 4 ; [7] § 34, 42, 48, 49, 55, 56, 78, 79, 86; [8]; [9]; [14]; [12].

Методичні вказівки. Завдання Д-2 на тему “Динамічні рівняння руху тіл”. Щоб застосувати цей метод , спочатку механічну систему роз’єднують на окремі тіла, враховуючи реакції в’язей між ними. Потім для кожного вільного тіла складається динамічне рівняння руху, форма якого залежить від виду руху тіла.

Якщо тіло виконує поступальний прямолінійний рух вздовж осі 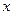, динамічне рівняння має вигляд:

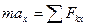, (Д2.1)

де 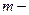маса тіла; 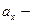проекція прискорення на вісь 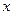; 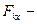проекція 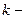ой сили на вісь .

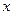Якщо тіло обертається навколо нерухомої осі 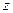, динамічне рівняння має вигляд:

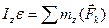, (Д2.2)

де 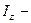осьовий момент інерції; 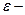кутове прискорення тіла; 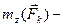момент сили 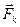відносно осі обертання .

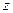Динамічні рівняння плоского руху тіла, коли центр мас (точка С) рухається вздовж осі 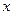, мають вигляд:

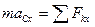(Д2.3)

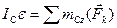(Д2.4)

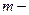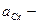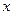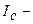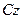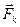де маса тіла; проекція прискорення центру мас тіла на вісь ; осьовий момент інерції тіла, відносно осі ; момент сили , відносно осі .

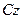Осьовий момент інерції диска або циліндра, маси яких розподілені по ободу радіуса 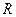(тобто момент інерції кільця), відносно центральної осі 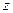дорівнює:

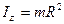(Д2.5)

Осьовий момент інерції однорідного диска, циліндра або котка радіуса 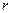відносно центральної осі 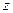визначається за формулою:

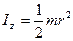(Д2.6)

Якщо задається радіус інерції тіла 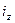відносно осі 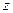, осьовий момент інерції тіла дорівнює:

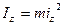(Д2.7)

Для того, щоб отримати динамічне рівняння руху механічної системи, необхідно із складених динамічних рівнянь руху тіл, з яких складається механічна система, виключити сили реакцій в’язей, бо для них має місце закон рівності дії та протидії.

Переглядів: 771