
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад Д-3
Механічна система (рис.Д3.а) складається з вантажу 1, ступінчастого шківа 2 з радіусами ступіней R2 і r2 (маса шківа рівномірно розподілена по зовнішньому ободу) та однорідного циліндричного котка 3. Коефіцієнт тертя між вантажем та площиною f. Тіла зв’язані між собою нерозтяжними нитками, намотаними на шків 2.
Під дією сили F =f(s), що залежить від переміщення вантажу 1, система починає рухатись із стану спокою. При русі на шків діє постійний момент сил опору М2.
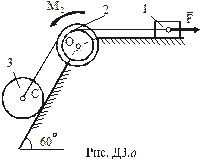 Дано:m1 = 4 кг, m2 = 10 кг, m3 = 8 кг,
Дано:m1 = 4 кг, m2 = 10 кг, m3 = 8 кг,
R2 = 0,2 м, r2 = 0,1 м, f = 0,2,
M = 0,6 Н м, F = 200(5+ 2s) H,
S1 =0,2 м.
Визначити: швидкість VC центра мас котка 3, коли переміщення вантажу 1 буде дорівнювати S1.
Розв’язування.
1. Розглянемо рух незмінної механічної системи, що складається з тіл 1, 2, 3, з’єднаних між собою за допомогою ниток (рис.Д3.б). Зобразимо всі діючи на систему зовнішні сили: активні 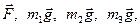 момент сил опору
момент сил опору  , реакції
, реакції 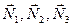 , сили тертя ковзання
, сили тертя ковзання 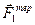 та тертя кочення
та тертя кочення 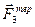 .
.
Для визначення VC використаємо теорему про зміну кінетичної енергії
механічної системи
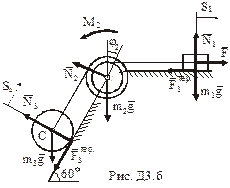
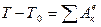 , (3.1)
, (3.1)
2. Визначимо 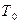 та
та 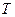 .
.
Кінетична енергія системи дорівнює сумі кінетичних енергій окремих тіл системи. Якщо в початковий момент часу система знаходилась у стані спокою, маємо:
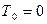
Для кінцевого положення системи, враховуючи, що тіло 1 виконує поступальний рух, тіло 2 – обертається навколо нерухомої осі, а тіло 3 – рухається в площині, маємо:
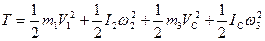 (3.2)
(3.2)
Момент інерції ступінчастого шківа, маса якого розподілена по його зовнішньому ободу, дорівнює:
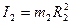 (3.3)
(3.3)
Момент інерції однорідного котка 3, визначається за формулою:
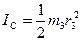 (3.4)
(3.4)
Виразимо всі швидкості через невідому швидкість центра мас котка 3 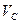 :
:
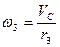 ,
,  ,
, 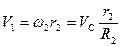 (3.5) Підставимо формули (3.3) – (3.5) у вираз (3.2) і отримаємо
(3.5) Підставимо формули (3.3) – (3.5) у вираз (3.2) і отримаємо
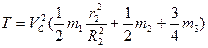 (3.6)
(3.6)
4. Тепер знайдемо суму робіт всіх діючих зовнішніх сил при переміщенні, яке буде мати система, коли вантаж 1 пройде шлях S1.
Робота сили 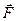 дорівнює:
дорівнює:

Роботи сили ваги 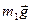 та реакції
та реакції 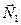 дорівнюють нулю, бо кут між цими силами та переміщенням S1 складає 900.
дорівнюють нулю, бо кут між цими силами та переміщенням S1 складає 900.
Між силою тертя ковзання 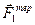 та переміщенням S1 кут 1800, тому A(
та переміщенням S1 кут 1800, тому A( 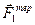 ) =
) = 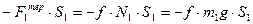 ,
,
де 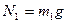 , бо вантаж знаходиться на горизонтальній площині.
, бо вантаж знаходиться на горизонтальній площині.
Момент М спрямований протилежно напрямку 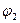 , тому його робота дорівнює
, тому його робота дорівнює
A(M) 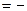 M
M 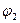
Роботи сили ваги 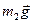 та реакції
та реакції 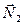 дорівнюють нулю, бо точка прикладання цих сил нерухома.
дорівнюють нулю, бо точка прикладання цих сил нерухома.
Робота сили ваги 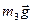 (кут між нею та переміщенням центра ваги катка
(кут між нею та переміщенням центра ваги катка 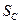 дорівнює 1500 ):
дорівнює 1500 ):
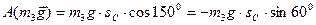 .
.
Точка прикладання сил 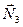 та
та 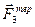 є миттєвим центром швидкостей, тому робота цих сил дорівнює нулю.
є миттєвим центром швидкостей, тому робота цих сил дорівнює нулю.
Таким чином, сума робіт діючих зовнішніх сил, що діють на систему на заданому її переміщенні:
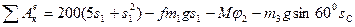 (3.7)
(3.7)
Виразимо всі переміщення через переміщення вантажу 1 S1:
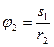 ;
; 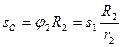 (3.8)
(3.8)
Підставимо (3.6) та (3.7) з врахуванням (3.8) в вираз теореми (3.1) та отримаємо:
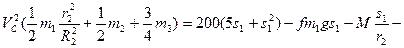
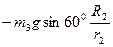 (3.9)
(3.9)
Підставимо чисельні значення та знайдемо швидкість центру ваги котка 3 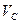
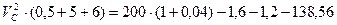
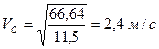
Відповідь: 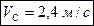
Завдання Д-4. Принцип Д’Аламбера
Умова завдання. Вертикальний вал 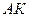 (рис. Д4.0 – Д4.9, табл. Д4), що обертається з постійною кутовою швидкістю
(рис. Д4.0 – Д4.9, табл. Д4), що обертається з постійною кутовою швидкістю 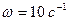 , закріплений підп’ятником в точці
, закріплений підп’ятником в точці 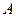 та циліндричним підшипником в точці, що вказана в табл. Д4 в стовпці 2
та циліндричним підшипником в точці, що вказана в табл. Д4 в стовпці 2 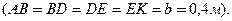 До вала жорстко прикріплені невагомий стержень 1 довжиною
До вала жорстко прикріплені невагомий стержень 1 довжиною 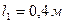 з вантажем масою
з вантажем масою 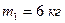 на кінці та однорідний стержень 2 довжиною
на кінці та однорідний стержень 2 довжиною 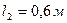 , що має масу
, що має масу 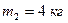 ; обидва стержня знаходяться в одній площині. Точки кріплення стержнів до вала та величини кутів
; обидва стержня знаходяться в одній площині. Точки кріплення стержнів до вала та величини кутів 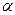 і
і 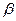 вказані в таблиці.
вказані в таблиці.
Визначити.Реакції підп’ятника та підшипника, нехтуючи вагою вала.
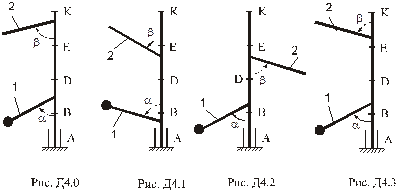
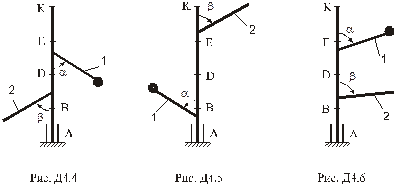
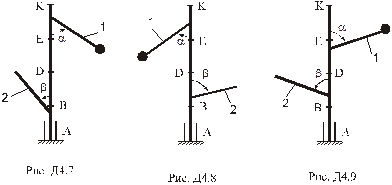
Табл.Д4
| Номер умови | Пiдшипник в точцi | Закрiплення | a° | b° | Номер умови | Пiдшипник точцi | Закрiплення | a° | b° | ||
| стержня 1 в точцi | стержня 2 в точцi | стержня 1 в точцi | стержня 2 в точцi | ||||||||
| B | D | K | D | K | B | ||||||
| D | B | E | E | B | K | ||||||
| E | D | B | K | E | B | ||||||
| K | D | E | D | E | K | ||||||
| B | E | D | E | K | D |
Теоретичне обґрунтування : [5] § 133 – 135 ; [6] Розд.III. Гл.5. § 1 ;
[7] § 106 - 111 ; [8]; [9]; [12]; [13].
Методичні вказівки. Завдання Д-4 на тему “Принцип Д’Аламбера для механічної системи». Введемо поняття сил інерції точки. Сила інерції 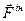 зумовлена прискореним рухом матеріальної точки, дорівнює добуткові маси точки на її прискорення і спрямована протилежно вектору прискорення. Тобто
зумовлена прискореним рухом матеріальної точки, дорівнює добуткові маси точки на її прискорення і спрямована протилежно вектору прискорення. Тобто
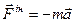 (Д4.1)
(Д4.1)
Згідно до основного закону динаміки точки:
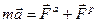 , (Д4.2)
, (Д4.2)
де 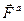 - рівнодійна активних сил,
- рівнодійна активних сил, 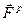 - рівнодійна сил реакцій в’язей.
- рівнодійна сил реакцій в’язей.
З (Д4.2) маємо: 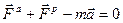
Або з урахуванням (Д4.1):
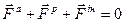 (Д4.3)
(Д4.3)
Вираз (Д4.3) є рівнянням умовної рівноваги точки, тобто рівноваги з урахуванням умовно прикладеної сили 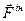 . Таким чином , принцип Д’Аламбера полягає в тому, що в кожний момент часу геометрична сума активних сил, сил реакцій в’язей, що діють на рухому матеріальну точку, та умовно прикладеної до точки сили інерції дорівнюють нулю.
. Таким чином , принцип Д’Аламбера полягає в тому, що в кожний момент часу геометрична сума активних сил, сил реакцій в’язей, що діють на рухому матеріальну точку, та умовно прикладеної до точки сили інерції дорівнюють нулю.
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад Д-2 | | | Приклад Д-4 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |