
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язування.
1. Розглянемо рух механічної системи, що складається з тіл 1, 2, 3, з’єднаних нитками. Система має один ступінь вільності, тобто існує одне незалежне переміщення, яке однозначно визначає положення системи. За узагальнену координату 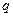 вибираємо переміщення тіла, прискорення якого треба знайти, тобто переміщення вантажу 1. Тоді узагальнена швидкість – це швидкість вантажу 1.
вибираємо переміщення тіла, прискорення якого треба знайти, тобто переміщення вантажу 1. Тоді узагальнена швидкість – це швидкість вантажу 1.
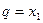 ;
; 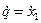
Запишемо рівняння Лагранжа II роду для обраної узагальненої координати:
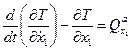 . (6.1)
. (6.1)
Визначимо кінетичну енергію системи, як суму енергій тіл системи. Враховуючи, що тіло 1 рухається поступально, шків 2 обертається навколо нерухомої осі, а рух котка 3 - плоский, отримаємо
 , (6.2)
, (6.2)
де моменти інерції шківа 2 (маса розподілена на зовнішньому ободі) і однорідного котка 3 радіусом 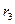 відповідно дорівнюють:
відповідно дорівнюють:
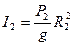 ,
, 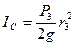 . (6.3)
. (6.3)
Виразимо швидкості, що входять в (6.2) через узагальнену швидкість. Врахуємо, що точка К (рис.Д6.б) дотику з похилою площиною для тіла 3 є миттєвим центром швидкостей:
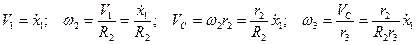 (6.4)
(6.4)
Підставимо (6.3) і (6.4) в рівняння (6.2), отримаємо:
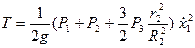 . (6.5)
. (6.5)
Кінетична енергія залежить тільки від узагальненої швидкості 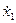 , тому, підставляючи (6.5) у ліву частину рівняння (6.1), отримаємо
, тому, підставляючи (6.5) у ліву частину рівняння (6.1), отримаємо
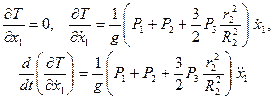 (6.6)
(6.6)
2. Визначимо узагальнену активну силу:
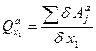 . (6.7)
. (6.7)
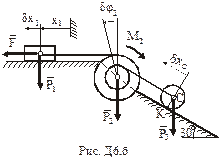 Зобразимо діючі на систему активні сили
Зобразимо діючі на систему активні сили 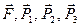 і момент
і момент 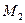 (рис.Д6.б). Задамо системі можливе переміщення, при якому узагальнена координата
(рис.Д6.б). Задамо системі можливе переміщення, при якому узагальнена координата 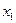 зростає, тобто
зростає, тобто  >0. Враховуючи напрямок можливого переміщення вантажу 1, покажемо можливі переміщення кожного з тіл: для тіла 2 – поворот на кут
>0. Враховуючи напрямок можливого переміщення вантажу 1, покажемо можливі переміщення кожного з тіл: для тіла 2 – поворот на кут 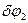 , для котка 3 – переміщення центру мас
, для котка 3 – переміщення центру мас 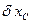 . Для визначення узагальненої активної сили обчислимо суму можливих робіт сил та моменту на заданому можливому переміщенні системи. Отримаємо:
. Для визначення узагальненої активної сили обчислимо суму можливих робіт сил та моменту на заданому можливому переміщенні системи. Отримаємо:
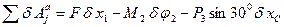 (6.8)
(6.8)
Виразимо всі можливі переміщення через  , враховуючи, що залежності між переміщеннями аналогічні залежностям (6.4) між швидкостями, і отримаємо:
, враховуючи, що залежності між переміщеннями аналогічні залежностям (6.4) між швидкостями, і отримаємо:
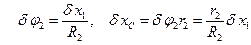 (6.9)
(6.9)
Остаточно, узагальнена активна сила, з урахуванням (6.8) і (6.9), буде мати вигляд:
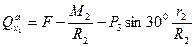 (6.10)
(6.10)
5. Підставимо (6.6) і (6.10) в рівняння Лагранжа II роду (6.1):
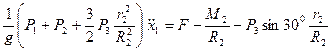 (6.11)
(6.11)
Підставимо числові значення та знайдемо прискорення вантажу 1 (вважаємо 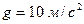 ).
).
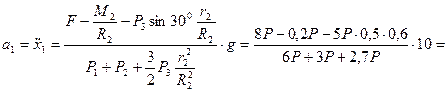
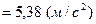
Відповідь: 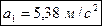 .
.
Завдання Д-7. Малі вільні коливання механічної системи
Умова завдання. Механізм, що розташований у вертикальній площині (рис. Д7.0 – Д7.9), складається із ступінчастих коліс 1 і 2 з радіусами 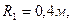
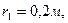
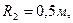
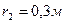 , що обертаються навколо нерухомих осей; однорідного стержня 3 довжиною
, що обертаються навколо нерухомих осей; однорідного стержня 3 довжиною 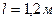 , закріпленого шарніром; вантажів 4 та 5, підвішених до ниток, намотаних на колеса. Маса коліс 1 і 2 розподілена на зовнішніх радіусах. Відстань
, закріпленого шарніром; вантажів 4 та 5, підвішених до ниток, намотаних на колеса. Маса коліс 1 і 2 розподілена на зовнішніх радіусах. Відстань 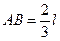 .
.
Стержень 3 з’єднаний з колесом 1 невагомим стержнем 6. Колеса 1 і 2 знаходяться в зачепленні або з’єднані невагомим стержнем 7. До коліс та стержня 3 прикріплені пружини.
В табл.Д7 задані маси 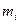 тіл та коефіцієнти жорсткості
тіл та коефіцієнти жорсткості 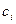 пружин. Прочерки в стовпцях означають, що відповідні тіла або пружини в систему не входять (на рисунку не зображати). Остаточно в кожному варіанті залишається простий механізм, що містить три або два тіла. Стержень 6 або 7 входять в склад механізму, коли до нього входять обидва тіла, що з’єднуються цим стержнем.
пружин. Прочерки в стовпцях означають, що відповідні тіла або пружини в систему не входять (на рисунку не зображати). Остаточно в кожному варіанті залишається простий механізм, що містить три або два тіла. Стержень 6 або 7 входять в склад механізму, коли до нього входять обидва тіла, що з’єднуються цим стержнем.
В положеннях, показаних на рисунках, механізм знаходиться в положенні стійкої рівноваги.
Визначити:
1. Частоту та період малих коливань системи біля положення рівноваги.
2. Статичну деформацію пружини 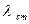 в положенні рівноваги.
в положенні рівноваги.
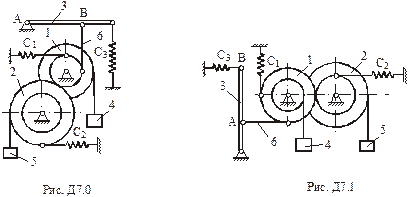
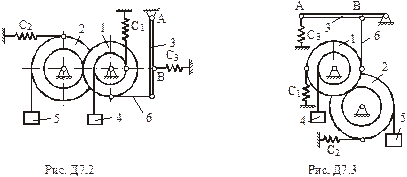
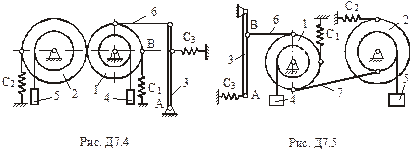
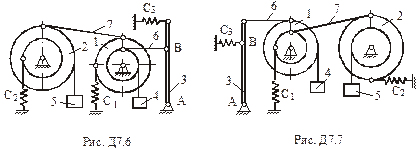
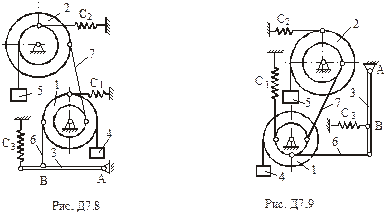
Табл.Д7
| Номер умови | m1, кг | m2, кг | m3, кг | m4, кг | m5, кг | c1, Н/м | с2, Н/м | c3, Н/м |
| - 10 | - - - | - - - - - - | - - - - - 4 | - - - - - - - | - - - - - | - - - - - - - | - - - - - - - - |
Теоретичне обґрунтування : [5] § 147, 148 ; [6] Разд.ІІІ. Гл.7. § 1-3 ;
[7] § 128 ; [8] , [9] , [13].
Методичні вказівки. Завдання Д-7 на тему “Малі лінійні коливання механічної системи поблизу положення рівноваги”. На систему діють тільки потенціальні сили, тому коливання будуть вільними. Для розв’язку задачі треба використати рівняння Лагранжа II роду:
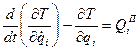 , (Д7.1)
, (Д7.1)
де 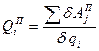 або
або 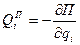 - узагальнена потенціальна сила;
- узагальнена потенціальна сила;
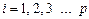 (
( 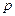 - кількість ступенів вільності системи);
- кількість ступенів вільності системи);
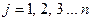 (
( 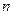 - кількість потенціальних сил, що діють на систему);
- кількість потенціальних сил, що діють на систему);
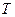 - кінетична енергія системи;
- кінетична енергія системи;
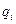 - і-та узагальнена координата;
- і-та узагальнена координата;
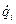 - і-та узагальнена швидкість;
- і-та узагальнена швидкість;
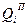 - узагальнена потенціальна сила, що відповідає і–ій узагальненій координаті (при розв’язуванні конкретних задач зручно позначати через
- узагальнена потенціальна сила, що відповідає і–ій узагальненій координаті (при розв’язуванні конкретних задач зручно позначати через 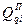 ).
).
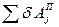 - сума можливих робіт потенціальних сил, що відбуваються на можливому переміщені системи за умовою, що
- сума можливих робіт потенціальних сил, що відбуваються на можливому переміщені системи за умовою, що 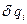 >0;
>0;
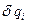 - можливе зростання узагальненої координати (
- можливе зростання узагальненої координати ( 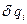 >0);
>0);
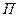 - потенціальна енергія системи.
- потенціальна енергія системи.
Кількість рівнянь Лагранжа II роду, що складається для розв’язування задачі, повинна дорівнювати кількості ступенів вільності, тобто кількості незалежних можливих переміщень, що має система.
У наведеному завданні система має один ступінь вільності, тому потрібно скласти лише одне рівняння Лагранжа ІІ роду. Після обчислення лівої і правої частини цього рівняння воно може бути записано у вигляді диференціального рівняння малих вільних коливань:
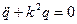 , (Д7.2)
, (Д7.2)
де 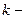 кругова частота малих вільних коливань.
кругова частота малих вільних коливань.
Період коливань визначається за формулою:
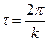 (Д7.3)
(Д7.3)
Розглянемо два приклада розв’язування цього завдання.
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад Д-6 | | | Приклад Д-7.1 |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |