Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Дифракція світла

Огинання хвилями перешкод називається дифракцією. Виникнення дифракції можна пояснити за допомогою принципу Гюйгенса: кожна точка хвильового фронту є джерелом вторинних сферичних хвиль, огинаюча яких дає положення хвильового фронту в наступний момент часу (див. рис. 73, а).

Промені світла поширюються вздовж нормалі до хвильового фронту. Тому дифракція світла призводить до проникнення світла в область геометричної тіні і утворення дифракційної картини – світлих і темних ділянок, які чергуються (див. рис. 73, б, в).

Дифракція дуже залежить від співвідношення розмірів перешкоди d на шляху світла і довжини хвилі l. Дифракція найбільш яскраво виражена при d»l.

Рис. 73

Принцип Гюйгенса-Френеля. Принцип Гюйгенса дозволяє тільки якісно пояснити явище дифракції, але не дозволяє визначити амплітуди розсіяних перешкодою хвиль, які поширюються в різних напрямках. Френель доповнив принцип Гюйгенса уявленням про інтерференцію вторинних хвиль. Врахування амплітуд і фаз вторинних хвиль дозволяє знайти амплітуду розсіяної перешкодою світлової хвилі в будь-якій точці простору.

Результуюче коливання в будь-якій точці спостереження P являє собою суперпозицію коливань, що проходять від усіх елементів хвильової поверхні S з урахуванням їх амплітуд і фаз:

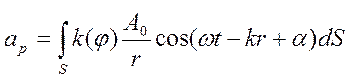, (6.9)

де 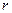– відстань від елемента dS хвильової поверхні 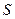до точки спостереження 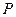(див. рис. 74), 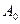– амплітуда коливань на елементі dS, w=2p /Т – циклічна частота коливань, k=2p/l – хвильове число. Отже результуюче коливання в точці Р дорівнює сумі (тобто інтегралу) коливань, що приходять в точку 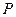від всіх елементів хвильової поверхні S з уврахуванням їх амплітуд і фаз. Це і є принцип Гюйгенса-Френеля.

Рис. 74

Види дифракції:

1) дифракція Фраунгофера, або дифракція в паралельних променях, коли відстані від джерела світла S до перешкоди, на якій відбувається дифракція, і відстань від перешкоди до точки спостереження P великі порівняно з розмірами перешкоди. При цьому промені, що падають від джерела світлу на перешкоду,

і промені, що поширюються від перешкоди в точку спостереження, йдуть практично паралельними пучками (див. рис. 75, а);

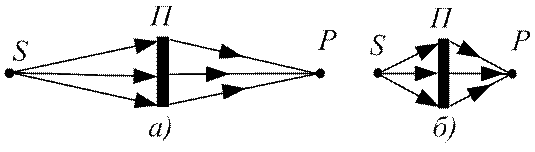
Рис. 75

2) дифракція Френеля – це дифракція в непаралельних променях, коли джерело світла і точка спостереження лежать недалеко від перешкоди (див. рис. 75, б)

Зони Френеля. Принципом Гюйгенса-Френеля (6.9) важко скористатися на практиці, оскільки важко підрахувати інтеграл по хвильовій поверхні S. Для полегшення цього Френель запропонував розбити поверхню інтегрування S (а це хвильова поверхня) на окремі ділянки, різниця ходу променів від меж яких дорівнює 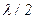. Ці ділянки хвильової поверхні отримали назву зон Френеля. Тоді результуючі коливання, що утворюються в точці спостереження Р вторинними хвилями від двох сусідніх зон Френеля, находяться у протифазі, тобто відрізняються за фазою на p. Тому амплітуда результуючого коливання, що утворюється в точці спостереження Р вторинними хвилями, які прийшли від всієї хвильової поверхні, визначається формулою.

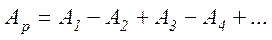, (6.10)

де А_m – амплітуда, утворена вторинними хвилями, які прийшли від m-ї зони Френеля.

Для точкового джерела світла хвильова поверхня сферична і зони Френеля для неї являють собою кільцеві області (крім першої) з радіусом зовнішньої межі

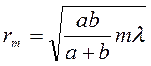де – радіус сферичної хвильової поверхні (див. рис. 76) – відстань від вершини сферичного сегменту (точка О) до точки спостереження Р (вимірюється уздовж лінії, яка з’єднує джерело S і точку спостереження Р).

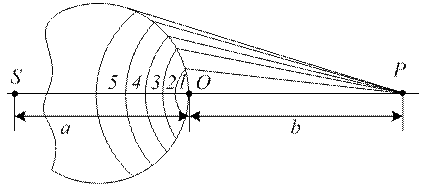
Рис. 76

Формулу (6.10) можна переписати у вигляді

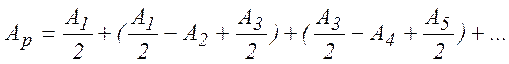
Для сферичної хвильової поверхні амплітуди А_m утворюють послідовність, що монотонно зменшується. Тому 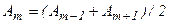і в результаті

, (6.11)

Тобто амплітуда, що утворюється в точці Р сферичною хвильовою поверхнею, дорівнює половині амплітуди, що утворюється однією центральною зоною.

Дифракція Френеля на круглому отворі. При дифракції сферичної хвилі на круглому отворі радіусу r₀ відкритими є 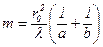зон Френзеля, де а – відстань від джерела світла до отвору, b – відстань від отвору до точки спостереження. Джерело S і точка спостереження Р лежать на осі симетрії отвору. Амплітуда коливань в точці Р

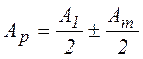де знак плюс береться, якщо кількість зон Френеля, що відкриває отвір, непарне, а знак мінус, якщо число зон парне. За малої кількості відкритих зон Френеля А₁»А_m і

За відсутності перешкоди A_p=A₁ /2 відповідно до формули (6.11). Таким чином, перешкода з отвором, який відкриває непарну кількість зон Френзеля, не тільки не послаблює світло, а навпаки, призводить до збільшення амплітуди коливань в точці Р у два рази, а інтенсивності коливань – у 4 рази. Це суттєво хвильовий ефект, який у межах геометричної оптики пояснити неможна.

При переміщенні точки спостереження у площині, паралельній площині з отвором, спостерігається дифракційна картина у вигляді світлих і темних кілець з максимумом у центрі, якщо отвір відкриває непарну кількість зон Френеля (див. рис. 77, а), і з мінімумом, якщо m – парне (див. рис. 77, б).

Рис. 77

На рис. 77 показані профілі інтенсивності світла залежно від відстані r від осі отвору. Якщо отвір відкриває не більше однієї зони Френеля, то на екрані розмита світла пляма.

Дифракція Фраунгофера на щілині. При дифракції паралельного пучка променів на щілині в екрані, промені розсіюються по всіх напрямках. Промені, які йдуть в одному напрямку, інтерферують між собою і в результаті на екрані спостерігається дифракційна картина. При нормальному падінні променів на щілину шириною b, різниця ходу крайніх променів, що йдуть під кутом дифракції j (цей кут відраховується від нормалі до площини щілини), дорівнює bsinj (див. рис. 78, а).

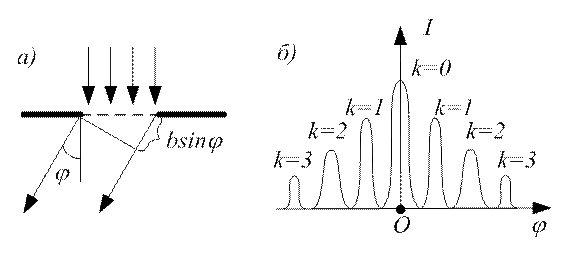
Рис. 78

Якщо виконується умова

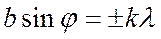, k=1,2,3,…, (6.12)

то хвильова поверхня на щілині розбивається на 2k (парну) кількість зон Френеля. Дії зон попарно компенсують одна одну і під даним кутом дифракції спостерігається дифракційний мінімум.

Якщо виконується умова

, k=1,2,3,…,

то на отворі вкладається 2k+1 (непарна) кількість зон Френеля. Дія однієї зони залишається незкомпенсованою і під даним кутом дифракції спостерігається дифракційний максимум.

Дифракційна картина являє собою чергування світлих і темних смуг. На рис. 78, б показано залежність інтенсивності дифрагованого світла від кута дифракції j. Під кутом j =0 всі вторинні промені накладаються в однаковій фазі і під цим кутом дифракції спостерігається головний дифракційний максимум (k=0). Світлі смуги дифракційної картини відповідають максимумам інтенсивності, а темні – мінімумам.

Дифракційні ґратки. Періодична послідовність щілин у екрані утворює дифракційну ґратку. Коливання, що поширюються від різних щілин ґратки, є когерентними і інтерферують. Результат накладання (підсумовування) коливань залежить від різниці фаз коливань для двох сусідніх щілин 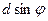, де 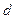– період дифракційної ґратки, – кут дифракції (див. рис. 79).

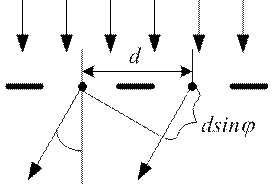
Рис. 79

За умови

, (6.13)

де m=0,1,2… – максимуми від окремих щілин накладаються в однаковій фазі і підсилюють один одного. Під такими кутами дифракції j спостерігаються головні дифракційні максимуми для ґратки. Формула (6.13) має назву формули дифракційної ґратки.

Умова (6.12) для дифракційних мінімумів для окремих щілин є одночасно і умовою для дифракційних мінімумів всієї ґратки.

Дифракційну картину при дифракції на ґратці пучка монохроматичного світла показано на рис. 80, а.

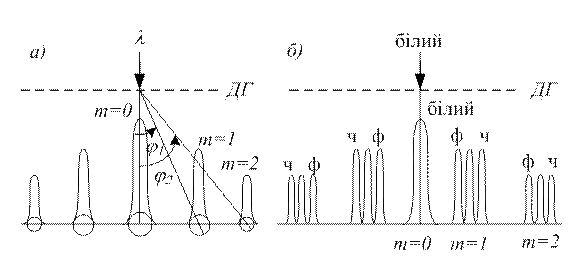
Рис. 80

Максимальний порядок (m) головних максимумів знаходиться з умови

Оскільки кут дифракції не може перевищувати 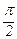, то кількість максимумів дорівнює 2m+1.

Положення головних максимумів залежить від довжини хвилі 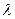. Тому при падінні на дифракційну ґратку білого світла всі максимуми дифракційної картини, крім центрального 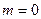, розкладаються у спектр (див. рис. 80, б). Амплітуда в головному максимумі дифракційної ґратки 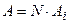, де 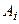– амплітуда у максимумі для окремої щілини, 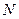– кількість щілин дифракційної ґратки. Тоді інтенсивність головних максимумів дифракційної ґратки 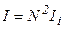. Тому максимуми дифракційної картини для ґратки дуже насичені і дифракційна ґратка вважається кращим спектральним приладом (тобто приладом для розкладання випромінювання у спектр).

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Інтерференція світла	\|	Поляризація

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.