• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Лінійні операції над векторами в координатній формі

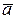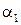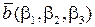Нехай заданий базис і вектори (,,), або, що те ж саме, , .

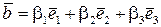Сума векторів.Запишемо суму векторів

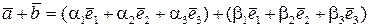
або, згідно властивостям лінійних операцій над векторами,

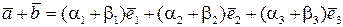. (5.3)

Таким чином, при додаванні векторів їх відповідні координати додаються.

Добуток вектора на число.Помножимо вектор 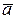на число :

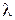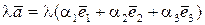
або

. (5.4)

Тобто при множенні вектора на число координати вектора множаться на це число.

Приклад 5.1.В базисі дано вектори 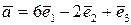, 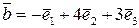. Знайти вектор .

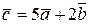Розв’язок. Згідно формулам (5.3), (5.4)

.

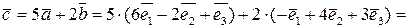
Відповідь: 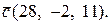t

Рівність векторів.З означення вектора як направленого відрізка, який можна переміщати в просторі паралельно самому собі, випливає, що два вектори 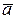і рівні тоді і тільки тоді, коли рівні їх координати:

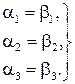
Колінеарність векторів.Вияснимо умови колінеарності векторів 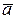і ,заданих своїми координатами.

Так як , то за властивостями добутку вектора на число можна записати 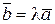, де 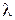– деяке число, тобто

.

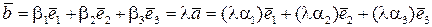Звідси , , , 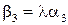тобт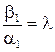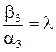о , , або

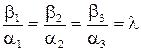. (5.5)

Таким чином, координати колінеарних векторів пропорційні. Справедливе і обернене твердження: вектори, що мають пропорційні координати, колінеарні.

Зауваження. Співвідношення (5.5) умовно записуватимемо і у випадку, коли серед чисел 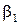, , 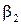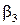є рівні нулю.

Нехай на площині заданий базис 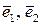і вектори 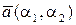, . В цьому випадку мають місце формули, аналогічні формулам (5.3) – (5.5).

Приклад 5.2.Перевірити, чи колінеарні вектори 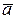і , задані в базисі :

а) , ; б) , .

Розв’язок. Згідно формули (5.5):

а) 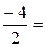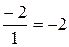, а отже .

б) .

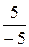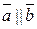Так як друга координата в обох векторів рівна нулю, то їх можна розглядати як вектори, задані на площині в базисі , а отже і . t

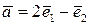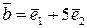Приклад 5.3.В базисі дано вектори , . Показати, що вектори утворюють базис, і знайти координати вектора в базисі .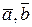

Розв’язок. Якщо два вектори утворюють базис, то вони неколінеарні. Згідно формули (5.5):

,

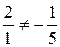а отже вектори 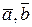неколінеарні і утворюють базис.

В новому базисі 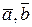вектор можна представити у вигляді лінійної комбінації

,

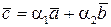де коефіцієнти 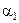, 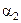– невідомі і є координатами вектора в базисі .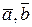

Знайдемо ці координати. Для цього розпишемо розклад вектора в координатній формі:

,

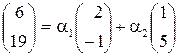що рівносильно системі двох лінійних рівнянь з двома невідомими

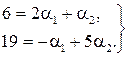
Розв’яжемо цю систему за формулами Крамера:

; .

Обчислимо визначники:

;

;

.

Отримаємо ; .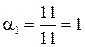

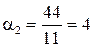Відповідь: 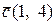. t

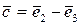Приклад 5.4.В базисі дано вектори , , . Показати, що вектори утворюють базис, і знайти координати вектора в базисі .

Розв’язок. Якщо три вектори утворюють базис, то жоден з них не є лінійною комбінацією двох інших. Тоді визначник, складений з координат цих векторів, відмінний від нуля, так як лінійні операції над векторами зводяться до відповідних лінійних операцій над їх координатами. Обчислимо цей визначник:

.

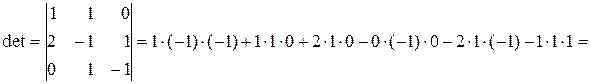
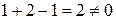Отже, вектори утворюють базис.

В новому базисі вектор 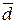можна представити у вигляді лінійної комбінації

,

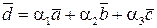де коефіцієнти 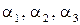– невідомі і є координатами вектора 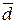в базисі .

Знайдемо ці координати. Для цього розпишемо розклад вектора 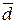в координатній формі:

,

що рівносильно системі трьох лінійних рівнянь з трьома невідомими

Розв’яжемо цю систему за формулами Крамера:

; ; .

Очевидно, що визначник 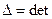як визначник транспонованої матриці:

.

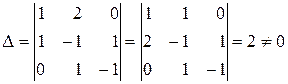Обчислимо

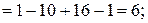
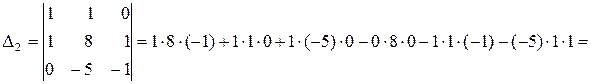
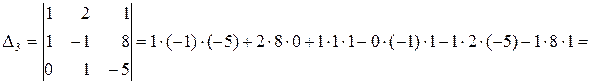
Отримаємо ; ;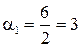

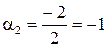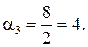
Відповідь: 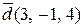. t

Читайте також:

1. Активні операції банків
2. Активні операції комерційних банків
3. Алгебраїчні операції
4. Арифметичні операції
5. Арифметичні операції в різних системах числення
6. Арифметичні операції над цілими числами
7. Багатоконтурні лінійні електричні ланцюги
8. Банк і його операції. Правова природа банківської діяльності
9. Бартерні операції
10. Білінійні і квадратичні форми в евклідовому просторі
11. Біржові операції.
12. Біржові операції. Котирування цін на біржі

Переглядів: 3539