Теоретичні відомості

ЛАБОРАТОРНА РОБОТА №9

Тема:«Вивчення загасаючих електромагнітних коливань»

Мета роботи: Ознайомлення із загасаючими електромагнітними коливання-ми в реальному коливальному контурі; визначення основних параметрів загасаючого коливання в експерименті.

Прилади та устаткування:Реальний коливальний контур (RLC), генератор прямокутних імпульсів, осцилограф, набір котушок індуктивності, конденсаторів та опорів.

Теоретичні відомості

Реальний коливальний контур складається з послідовно з'єднаних кон-денсатора С, котушки індуктивності L і резистора R. Якщо зарядити конденсатор С такого контуру, то при відсутності зовнішніх джерел е.р.с. він почне розряджатися і в контурі виникне струм, який буде змінюватися з часом за гармонічним законом. Коли заряд конденсатора дорівнюватиме нулю, струм у контурі досягне максимуму. Потім струм почне спадати, не змінюючи свого напрямку, що приведе до перезарядження конденсатора. Причиною поступового, а не стрибкоподібного зростання та зменшення струму в контурі є е.р.с. самоіндукції, що виникає в котушці при зміні сили струму в контурі. Ця ж е.р.с. спричиняє перезарядження конденсатора і, отже, є причиною виникнення коливань у контурі. Якщо активний опір контуру дорівнює нулю, коливання в ньому будуть незагасаючими.

Активний опір R реального контуру не дорівнює нулю. 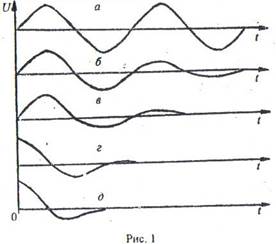Тому завжди є втрати електричної енергії на нагрівання провідників (опорів). У такому контурі амплітуда коливань буде поступово зменшуватись і врешті-решт коливання припиняться. Такі коливання називають загасаючими (рис. 1,а,б). Чим більший активний опір контуру тим активніший процес загасання (рис. 1, в).

Якщо величина активного опору контуру R перевищує деяке значення, що називається критичним, коливання в контурі взагалі не будуть збуджуватися. Заряд q конденсатора при цьому буде монотонно зменшуватися і асимптотично наближатися до нуля.

Виходячи з умови квазістаціонарності струму в коливальному контурі, маємо:

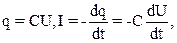(1)

де q - заряд конденсатора в даний момент часу, , U - різниця потенціалів на його обкладинках, I – сила струму в контурі. Знак "-" означає, що позитив-ному напрямку струму відповідає зменшення заряду конденсатора. Виведемо рівняння електричних коливань у контурі при наявності активного опору. Згідно з законом Ома маємо:

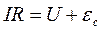(2)

де 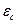- е.р.с, самоіндукції в котушці: 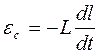(3)

Підставляючи значення е.р.с. самоіндукції та струму, у рівняння (2), отримаємо:

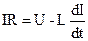Поділимо ліву і праву частини рівняння на LC та введемо позначки:

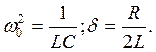
Після цих перетворень маємо диференціальне рівняння вільних коливань у реальному коливальному контурі при відсутності зовнішньої е.р.с.:

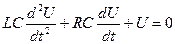або
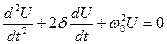(4)
Рішення цього диференціального рівняння другого порядку (тобто залежність напруги U на конденсаторі коливального контуру від часу ) має вигляд

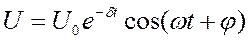(5)

де ω=√ω₀²-δ²;U₀ і φ - постійні, що визначаються початковими умовами.

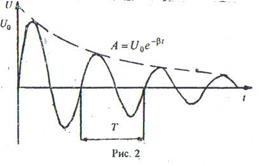Графік цієї залежності наведений на рис.2.

Знього видно, що значення напруги на конденсаторі періодично проходять через нуль і максимальні величини. Проміжок часу Т називають періодом затухаючих коливань

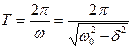
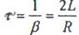а величину 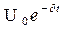– амплітудою

загасаючих коливань. За час амплітуда коливань зменшується в "е" разів (e-основа натуральних логарифмів, що дорівнює 2,718…). Час τ зветься часом релаксації коливального контуру.

Ступінь загасання прийнято характеризувати логарифмічним декрементом загасання, який дорівнює натуральному логарифму відношення двох послідовних максимумів амлітуди:

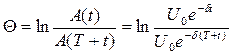(6)

Цей параметр пов’язаний з числом коливань N, що відбуваються за час релаксації τ, залежністю

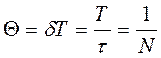(7)

Важливою характеристикою загасаючих процесів у контурі є його

добротність Q. При незначному затуханні (δ<<ω₀²) добротність можна обчислити за формулою:

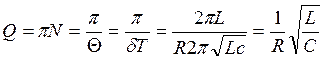(8)

<== попередня сторінка	\|	наступна сторінка ==>
Вихідний текст програми CGI store.exe	\|	Опис установки

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.016 сек.