• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Відношення.

Відношення - це будь-який зв’язок між предметами або поняттями множин.

Поняття відношення - чисто математичне поняття, яке не вживається для вказання зв’язків у інших сферах застосування. В цих сферах використовують поняття відносини, взаємини, стосунки.

Відношення між двома елементами називається бінарним.

Способи задання відношень. Якщо є деякий елемент х і деякий елемент у і між цими елементами встановлюється будь-який зв’язок, тобто. відношення, то це відношення записується так:

х R у - х і у знаходяться в деякому відношенні R.

(х, у) Î R - пара елементів х і у належать відношенню R.

х - називають лівим полем відношення

у - називають правим полем відношення

Приклад:

· (3 і 7)Î<; 3<7

елементи 3 і 7 належать відношенню упорядкування, тобто 3 менше 7.

· (Україна, Росія)Îсусіди.

В загальному випадку, якщо елемент х належить множині Х, а у належить множині У, то відношення R може бути задано на множинах Х і У як підмножина декартового добутку множин Х Ä У

х Î Х , у Î У Þ R Ì Х Ä У

Наприклад:

Х- множина країн СНД

У- множина країн ЄС

R- відношення між країнами СНД і ЄС тобто договори про економічне співробітництво (торгівля ).

Для задання відношень на скінчених множинах Х та У, часто використовують графічну форму (графові форми).

При графовому поданні, елементи множин Х та У позначають точками, а наявність відношення R між певними елементами позначають лінією-стрілкою, яку називають направленою дугою.

Наприклад:

Х={х₁, х_2,, х_3,, х₄, х₅}

У={у₁, у₂, у₃}

R={(х₁, у₁), (х₁, у₂), (х₂, у₂), (х₂, у₃), (х₃, у₁), (х₄, у₅), (х₅, у₁), (х₅, у₃)}

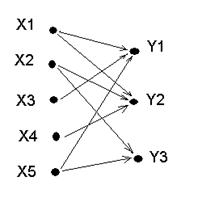
Це графічне відношення від Х до У (біграф).

Часто застосовують матричну форму задання відношень.

Матриця - прямокутна таблиця, в якій рядки відповідають опису вершин множини Х, а стовпці відповідають опису вершин множини У.

Елементи матриці приймають значення “О” або “1”.

“1”- якщо відповідний елемент матриці, який знаходиться на перетині рядка і стовпця належить відношенню R.

“0”- якщо відповідний елемент матриці, який знаходиться на перетині рядка і стовпця не належить відношенню R.

Матричний спосіб задання відношення від Х до У:

;

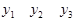
Таку матрицю називають матрицею відношень.

Обернене відношення (транспонована матриця)позначають R^-1:

.

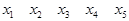
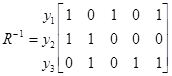Множину всіх перетинів відношення R називають фактор-множиноюмножини У по відношенню R і позначають У/R.

Побудуємо матрицю підстановки, яка складається з двох рядків, а кількість стовпців відповідає елементам множини Х. В першому рядку записують елементи лівого поля (в нашому випадку множини Х). В другому рядку, під кожним елементом множини Х записують фактор-множину множини У(У/R).

.

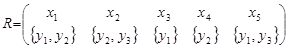Приклад:

Х={х₁, х₂, х₃, х₄, х₅}

х₁ - Росія

х₂ -- Україна

х₃ - Іран R- відношення торгівлі зброєю.

х₄ - Пакистан

х₅ - Кувейт

Задане аналітичне відношення. Формуємо графічне та матричне відношення.

R={(х₁, ,х₂), (х₁,х₃), (х₁,х₄) ,(х₂,х₁), (х₂,х₄), (х₂,х₅), (х₃,х₅), (х₄,х₅)}

;

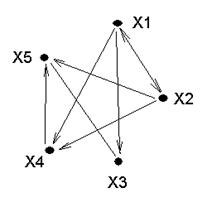
Відношення називається симетричним в тому випадку, якщо кожному елементу відношення х R у можна поставити у відповідність кожний елемент у R х..

Наприклад: (Україна, Росія) є сусіди.

Композиція відношень. Нехай дано три X, Y, Z та два відношення

R₁ Ì X Ä У та R₂Ì У Ä Z. Композиція відношень R₁ та R₂ є відношення R, яке складається з усіх тих пар (x, y) Ì X ´ Z, для яких існує таке y Î Y, що

(x, y) Î R₁ та (y, z) Î R₂.

Перетин відношення R по х співпадає з перетином R₂ за підмножиною R₁(x) Ì Y, тобто R(x) = R₂(R₁(x)).

Властивості відношень.

Розглянемо основні властивості бінарних відношень, що широко використовуються при описі взаємозв’язків об’єктів в задачі прийняття рішень:

Нехай R - якесь бінарне відношення, задане на множині X.

R={ / (x_i, x_j) володіють властивістю / }

1. Відношення R називається рефлексивним, якщо для будь-якого елемента цього відношення (x_i, x_j)ÎR випливає, що (x_i, x_i)ÎR. Тобто ця властивість значить, що об’єкт знаходиться у деякому відношенні R до самого себе. В матриці по головній діагоналі будуть одиниці.

Наприклад:

Х={x₁, x₂, x₃, x₄, x₅};

R={(x₁, x₂), (x₁, x₅), (x₃, x₄), (x₁, x₁), (x₂, x₂), (x₃, x₃), (x₄, x₄), (x₅, x₅)}

Графічне задання рефлексивного відношення:

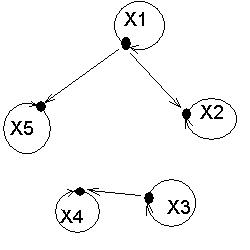
2. Антирефлексивність - з x_i R x_j випливає що, x_i ¹ x_j, тобто властивість антирефлексивності може виконуватися, тільки для неспівпадаючих об’єктів : (x_{i ,}, x_j) Î R, (x_{i ,}, x_i) ÏR . На головній діагоналі нулі.

3. Симетричність - якщо x_i R x_j, то і x_j R x_i, тобто відношення симетричне до обох об’єктів R Í 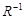(наприклад спільні кордони).

4. Антисиметричність - якщо одночасно x_i R x_j та x_j R x_i, тобто це значить, що x_i = x_j . Нестрога нерівність «£», включення. Наприклад множина А є підмножиною множини В.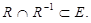

5. Трназитивність - якщо x_i R x_j та x_j R x_k, то x_i R x_i .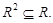

Використовуючи ці властивості, можемо визначити відношення еквівалентності, строгого порядку та нестрогого порядку. Наявність властивості є ознакою для визначення типа відношення. Наприклад відношення еквівалентності називається рефлексивне, симетричне, транзитивне відношення.

Відношення еквівалентності можемо назвати як взаємозаміняємість , однаковість об’єктів.

Відношення строгого порядку є антирефлексивним та транзитивним відношенням (тобто віддання переваги) x_i > x_j .

Відношення нестрогого порядку - є об’єднання відношень строгого порядку та еквівалентності. Володіє властивостями рефлексивності, антисиметричності та транзитивності. Це означає, що об‘єкт х_і або строгої переваги або еквівалентності об’єкту x_j , тобто об’єкт х_і не гірше x_j.

Різноманітність будь-яких об’єктів, показників порівнянь та видів відношень, привело до необхідності встановлення універсальної системи з відношеннями. В якості такої системи використовують числову систему.

Повний граф - коли всі вершини попарно зв’язані.

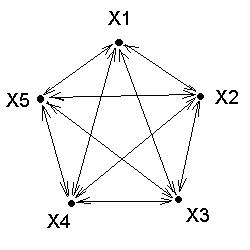
У матриці повного графу всі елементи одиниці, крім елементів головної діагоналі, які приймають значення нуля.

.

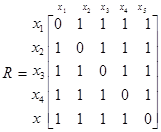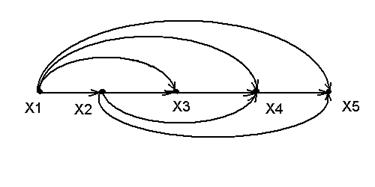
Функціональні відношення - коли всі його елементи , тобто пари, мають різні ліві координати:

R = {(x₁, x₄), (x₂, x₃), (x₃, x₅), (x₄, x₂), (x₅, x₁)}

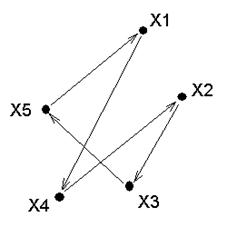
Це граф - коли з кожної вершини тільки один зв’язок.

Функціональне відношення. Відношення R Ì X* Y називається функціональним, якщо усі його елементи (упорядковані пари) мають різні перші координати. Кожному елементу х з Х такому, що (х, у) Î R відповідний один і тільки один елемент у з Y.

Типи відображень

1. Якщо кожен елемент множини У є значенням (образом) якого-небудь елемента з множини Х, то кажуть, що в цьому випадку є сур’єкція (покриття) множини Х на множину У.

2. Якщо для любих елементів х множини Х їх образи різні, то відображення R називається ін’єкцією множини Х на множину У.

3. Відображення, якому властиві одночасно сур’єкція і ін’єкція, називається бієкцією, або взаємно-одночасне відображення (це коли кількість елементів в множині Х та У співпадають).

Читайте також:

1. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
2. Використаємо це співвідношення. Тоді
3. Логічна норма права і текст нормативного акту: співвідношення.
4. Нормативно-правові акти, акти застосування права та інтерпретаційні акти: співвідношення.
5. Поняття бінарного відношення. Способи перетворення бінарних відношень і дії над ними
6. Права людини і громадянина: співвідношення.
7. Правосуб'єктність фізичних осіб - це передбачена нормами права здатність (можливість) осіб бути учасниками правовідношення.
8. Структуроформуючі відношення.

Переглядів: 6099