• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Множення матриць.

Означення. Множення матриці А на матрицю В можна здійснити тоді і тільки тоді, коли число стовпців матриці А відповідає числу рядків матриці В.

Нехай задано дві матриці А розміром (m ´ n) та В розміром (n ´ r).

Означення. Добутком А*В називається матриця С розміру (m ´ r), елементи якої c_ij дорівнюють сумі добутків елементів і - го рядка матриці А на відповідні елементи j-го стовпця матриці В, тобто елементи матриці С знаходяться за формулою

c_ij = a_i1b_1j + a_i2b_2j + a_i3b_3j + ...+ a_ikb_kj+ ... +a_inb_nj = ,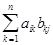

().

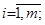
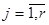Приклад. Обчислити А*В, якщо

А =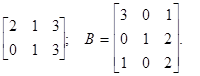

Розв’язок

A * B =

Очевидно, що для квадратних матриць операція множення справедлива, коли матриці мають однакові порядки.

Окремі схеми множення:

n матриці на стовпець (отримуємо матрицю стовпець):

А_m´n×· B_n´1 = C_m´1;

n рядок на матрицю (отримаємо матрицю рядок):

A_1´n · B_n´n = C_1´n;

n рядок на стовпець (отримаємо елемент):

A_1´n · B_n´1 = C_1´1 ;

n стовпець на рядок (отримаємо прямокутну матрицю):

A_m´1 · B_1´n = C_m´n.

Степінь матриць. Операція множення матриць розповсюджується на випадок декількох співмножників. На підставі цього для квадратних матриць можна ввести поняття степеня матриці. Щоб піднести квадратну матрицю до степені, необхідно (k -1) раз виконати множення матриці:

A² = A · A; Aⁿ = ,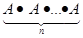

Приклад

А³ =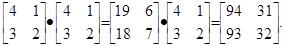

Читайте також:

1. Аксіоми додавання і множення
2. Безстатеве розмноження та його біологічне значення
3. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
4. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
5. Диференціювання та інтегрування матриць.
6. Додавання матриць.
7. Додавання, віднімання, множення і ділення цілих чисел. Теореми про існування та єдиність цих операцій. Закони операцій додавання і множення.
8. Економіко-правові проблеми примноження національного багатства.
9. Загальна характеристика дроб’янок, їх класифікація. Ціанобактерії. Будова та форми клітин справжніх бактерій. Способи живлення і розмноження бактерій
10. Існує багато способів зберігання розріджених матриць.
11. Множення і ділення невід’ємних раціональних чисел. Теореми про існування та єдиність добутку та частки. Властивості (закони) множення.
12. Множення імовірностей

Переглядів: 6685