• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Однорідні системи лінійних алгебраїчних рівнянь.

Означення. Лінійне рівняння називається однорідним, якщо вільний член рівняння дорівнює нулю. Система, яка містить однорідні рівняння, називається однорідною.

Загальний вигляд однорідної системи m рівнянь з n невідомими подається у вигляді:

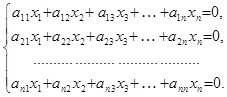
Відзначимо, що однорідна система завжди сумісна, оскільки має принаймні один розв’язок: x₁ = x₂ =...= x_n = 0.

Означення. Якщо однорідна система має один розв’язок, то він буде нульовим, і система називається тривіальною.

Означення. Якщо однорідна система має більше, ніж один розв’язок, то серед них є ненульові, і в такому випадку система називається нетривіальна сумісна.

Означення. Однорідна система буде мати нетривіальні розв’язки тоді і тільки тоді, коли її ранг r матриці коефіцієнтів системи менше числа n її стовпців.

Тема 5. Теорія графів

Історична довідка.

Виникнення теорії графів пов’язують з іменем Леонарда Ейлера, який у 1736 р., коли працював в Російський Академії наук, не тільки розв’язав популярну на той час головоломку про кенігсбергські мости, а й знайшов критерій існування в графі спеціального маршруту (ейлерового циклу). Це задача про те чи можливо здійснити прогулянку таким чином, що якщо вийти з будь-якого місця міста повернутися в нього, проходячи один раз по кожному мосту? Місто Кенігсберг (Калінінград) розташовано на чотирьох частинах суші a, b, c, d тому їх було представлено у вигляді вершин, а сім мостів зображені ребрами, які з’єднують відповідні вершини. В результаті отримали граф (рис.1). Ейлер довів, що подібний маршрут має бути тільки для графа у якого кожна вершина зв’язана парним числом ребер .

Рис. 1.

Теорія графів має потужний апарат рішення прикладних задач у самих різних сфер науки. До яких відносяться, наприклад теорія зв’язку, аналіз систем, проектування обчислювальних машин, архітектура, дослідження операцій, генетика, психологія, соціологія, економіка і т.д. Теорія графів також тісно пов’язана з такими розділами математики, як теорія множин, теорія матриць, математична логіка та теорія ймовірності. В усіх цих розділах графи застосовуються для представлення різних об’єктів.

В останні роки з’явилися дослідження, що показують особливе значення графів у сучасному суспільстві. Будь-який ринок (інформаційний) - це графова система зі своїми структурними елементами у вигляді покупців, продавців, пунктів продажу.

Час, у якому ми живемо, часто називають століттям глобалізації чи інформаційним століттям, підкреслюючи якісно нове значення інформації в ньому. Якісно нову роль отримали в новому часі і багато організаційних структур, переважну більшість яких організовано за принципом графів. Будь-які комунікаційні системи, організовані за принципом графів.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. II. Критерій найбільших лінійних деформацій
5. IV. Розподіл нервової системи
6. IV. Система зв’язків всередині центральної нервової системи
7. IV. Філогенез кровоносної системи
8. POS-системи
9. VI. Філогенез нервової системи
10. Автокореляційна характеристика системи
11. АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ
12. АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ ДОРОЖНІМ РУХОМ

Переглядів: 1562