Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Властивості матриці інцидентності

- кожний стовпець матриці інцидентності обов’язково містить два одиничних елемента (для орграфа вони мають різні знаки);

- кількість одиниць в рядку дорівнює степені відповідної вершини (для орграфа - кількість одиниць зі знаком «+» визначає позитивну напівстепінь, кількість одиниць зі знаком «-» – негативну напівстепінь;

- нульовий рядок відповідає ізольованій вершині;

- нульовий стовпчик відповідає петлі.

Суміжність. Задання графа за допомогою матриці суміжності.

Матриця суміжності графа — це квадратна матриця A=_ , стовпцям і рядкам якої відповідають вершини графа. Для неорієнтованого графа a_ij дорівнює кількості ребер, інцидентних i-та j -й вершинам, для орієнтованого графа цей елемент матриці суміжності відповідає кількості ребер з початком в і-й вершині й кінцем j -й. Таким чином, матриця суміжності неорієнтованого графа є симетричною (a_ij = a_ji), а орієнтованого — необов'язково. Якщо вона все ж симетрична, то для кожного ребра орієнтованого графа існує ребро, яке з'єднує ті самі вершини, але йде у зворотному напрямку. Очевидно, орієнтований граф із симетричною матрицею суміжності канонічно відповідає неорієнтованому графу, що має ту саму матрицю суміжності.

Таблиця 2.

	v₁ v₂ v₃ v₄ v₅
v₁ v₂ v₃ v₄ v₅	_

Властивості матриці суміжності

- матриця суміжності не орієнтованого графа завжди симетрична до головної діагоналі.;

- елементи на головній діагоналі завжди дорівнює 0, тільки коли є петля тоді елементи на головній діагоналі дорівнює 1;

- матриця суміжності орієнтованого графа в загальному випадку не симетрична відносно головної діагоналі;

- в стовпчиках або рядках, відповідних ізольованим вершинам, усі елементи дорівнюють 0.

Локальні степені вершин графа

Якщо задано матриці суміжності А або інцидентності S графа, то можна визначити локальні степені всіх його вершин. Справді, в j-му стовпці матриці інцидентності, що відповідає вершині v_j одиниці знаходяться на перетині з рядками, яким відповідають інцидентні цій вершині ребра, а інші елементи стовпця дорівнюють 0. Отже,

r (v_i) = _.

Елементи ж a_ij матриці суміжності — це кількість ребер, інцидентних вершинам v_t і v_j. Звідси

_r (v_j) = _.

При підрахунку степенів вершин за цими формулами кожна петля вносить у степінь інцидентної їй вершини 1. Проте при зображенні петлі на рисунку до цієї вершини примикають два кінці петлі, тобто петля вносить у цей степінь 2. Щоб таким чином ураховувати внесок петель у степінь, треба трохи ускладнити формули для його обчислення. Через коефіцієнти матриці інцидентності степінь можна розрахувати, наприклад, за формулою

r`(v_j) = . Коли і -те ребро звичайне, _,

і відповідний доданок зовнішньої суми дорівнює s_ij, тобто 1 для ребер, інцидентних вершині v_j,, та 0 для інших. Якщо ж воно є петлею, то_ =1, а доданок зовнішньої суми дорівнює 2s_ij , тобто 2 для петель, Інцидентних вершині v_j , та 0 для інших.

Це саме значення степеня визначається через коефіцієнти a_ij матриці

суміжності графа G за формулою

p'(v_ij ) = _.

Залежно від задачі, що розглядається, може бути потрібен той чи інший спосіб визначення степеня вершини. Тому в кожному випадку має бути відомо, чи є петля один раз або двічі інцидентною своїй вершині.

Оскільки кожне ребро має два кінці, в сумі _ ребра врахову-

ються двічі. Таким чином, ця сума дорівнює подвоєному числу ребер графа, тобто є парною. Отже, парна також кількість непарних доданків цієї суми, тобто кількість вершин непарного степеня.

Означення.Граф називається однорідним степеня k, якщо степені всіх його вершин дорівнюють k і, отже, є рівними між: собою.

Якщо однорідний граф степеня k має п вершин та т ребер, то

m = .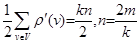

Означення .Звичайний граф називається повним, якщо кожна пара

його вершин сполучається ребром.

У звичайного повного графа Р_п на п вершинах степені всіх вершин однакові й дорівнюють п - 1.

Степінь ізольованої вершини r (v_i) = 0. Вершина зі степеню r (v_i) = 1 називається кінцевою чи висячою вершиною.

Локальні степені вершин орієнтованих графів

Для вершин орієнтованого графа визначаються два локальних степеня: r₁ (v) - кількість ребер із початком у вершині v, або, інакше, кількість ребер, які виходять із v, і r₂ (v) — кількість ребер, що входять у ребра v, тобто ребер, для яких ця вершина є кінцем. Петля дає внесок 1 в обидва ці степені. Локальні степені вершин орієнтованого графа визначаються через коефіцієнти a_ij його матриці суміжності:

r₁ (v_i ) = _, r₂ (v_i ) = _.

Вираз їх через коефіцієнти матриці інцидентності — значно складніший. Оскільки кожне ребро орієнтованого графа G має один початок й один

кінець, суми r₁ (v) і r₂ (v) дорівнюють кількості ребер цього графа, а отже, є рівними між собою. Звідси випливає, що в однорідному орієнтованому графі степеня k з п вершинами й т ребрами

m = _

Частини графа, суграфи та підграфи

Означення.Граф G`= (V`, E`) - називається частиною графа G = (V, E) (G`Ì G), якщо множина його вершин V` міститься в множині V, а множина Е` ребер - в Е. Якщо V` = V, то частина графа називається су- графом.

Означення. Граф G`= (V`, E`) - називається частиною графа G = (V, E) (G`Ì G), якщо V` Ì V та E` Ì E, тобто граф містить усі вершини і ребра будь-якої його частини. Частина, яка містить певну підмножину ребер графа та усі інцидентні їм вершини, називається підграфом або компонентом вихідного графа..
Приписування вершинам, ребрам та дугам графа деяких кількісних ознак або характерних властивостей називається. вагою і дозволяє отримати зважений граф.

Велике значення для моделювання мають зважені орієнтовані графи, які називаються. сигнальними графами.

Вершини сигнального графа ототожнюються з будь-якою змінною, яка характеризує стан системи, вага кожної вершини означає функцію часу або інші величини, які характеризують відповідні змінні.

Дуги відображають зв’язок між змінними а вага дуги представляє собою кількісне чи функціональне відношення, яке характеризує передачу сигналу від однієї вершини до другої.

Маршрути, цикли, зв’язність.

Інколи на графі необхідно виділити маршрут довжиною m.

МаршрутомMу заданому графі G = (V, Е) називається скінченна послідовність його ребер, яка має вигляд

(v₁, v₂), (v₂,, v₃), ..., (v_m-1, v_m).

Число m ребер маршруту M називається довжиною цього маршруту. Часто можна зустріти і таке означення маршруту в графі: послідовність вершин

v₁, v₂, ..., v_m графа G = (V, Е) називається маршрутом M,який з'єднує вершини v₁ і v_m.. В обох випадках вершини v₁, v₂, ..., v_m називаються вершинами маршруту.

Очевидно, що відношення маршрут, який з'єднує вершини., є симетричним і транзитивним.

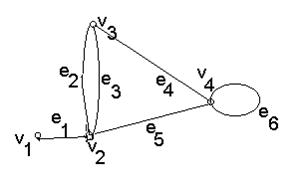
Рис. 8. Граф.

Прикладами маршрутів на графі рис.8 може бути послідовність {e₁, e₂, e₃, e₂, e₄ }, {e₄, e₆, e₅}. Перший маршрут проходить через послідовність вершин {v₁, v₂, v₃, v₂, v₃, v₄ } і з’єднує вершини v₁ і v₄ , а другий - через послідовність вершин {v₃, v₄, v₄ } і з’єднує вершини v₃, v₄ .

Замкнутий маршрут приводить в ту ж вершину, з якої почався.

Маршрут називається ланцюгом,якщо всі його ребра різні, і простим ланцюгом,якщо всі його вершини, крім, можливо, першої і останньої, різні.

Так на графі рис.8. {e₂, e₄, e₆} - ланцюг, {e₁, e₂, e₄} - простий ланцюг.

Маршрут називається циклічним,якщо перша і остання його вершини збігаються.

Цикломназивається циклічний ланцюг, а простим циклом-простий циклічний ланцюг. Так на графі рис.8. {e₂, e₄, e₅} - простий цикл.

Означення зв'язного графа. Граф називається зв'язним,якщо довільні дві його вершини зв'язані маршрутом (а згідно з твердженням 1 можна сказати — і простим ланцюгом). Зв'язний підграф G` графа G називається максимальним,якщо G` не міститься в жодному зв'язному підграфі графа G. Максимальний зв'язний підграф графа називається компонентом зв'язності.

Властивості зв’язних графів.

Часто виникає питання про число ребер зв'язного графа.

Нехай G = (V, Е) — граф з п вершинами і k компонентами зв'язності. Якщо такий граф зв'язний, то природно чекати, що число ребер у ньому мінімальне, коли він ациклічний, і максимальне, коли він повний. Звідси випливає така оцінка для числа ребер зв'язного графа:

n - 1 £ êE ê £ n× (n - 1) /2.

Нехай G — граф з п вершинами і k компонентами зв'язності. Тоді число т його ребер задовольняє нерівності

n - k £ m £ (n - k) × (n - k + 1) / 2.

Будь-який граф порядку п, який має більше (л - 1) × (n- 2)/2 ребер, зв'язний.

Дійсно, в цьому випадку число компонентів зв'язності такого графа повинне бути строго менше двох. Отже, k = 1, тобто граф зв'язний.

Властивості ейлерових графів.

Одним з важливих різновидів зв'язних графів є так звані ейлерові і гамільтонові графи.

Зв'язний граф G називається ейлеровим,якщо існує замкнутий ланцюг, який включає кожне його ребро. Такий ланцюг називається ейлеровим ланцюгом.(циклом). Цикл, який містить усі ребра графа, називається ейлеровим циклом (існує для непарної кількості вершин).

Зв'язний граф G називається напівейлеровим,якщо в ньому існує ланцюг, який включає кожне його ребро. Таким чином, всякий ейлерів граф буде напівейлеровим.

Теорема.Зв'язний граф G є ейлеровим тоді і тільки тоді, коли кожна вершина G має парний степінь.

Зв'язний граф ейлерів тоді і тільки тоді, коли множину його ребер можна розбити на цикли, що не перетинаються.

Зв'язний граф напівейлерів тоді і тільки тоді, коли він має не більше двох вершин непарного степеня.

Зауважимо, що теорема справедлива для псевдографів (які мають 4 петлі) і для мультиграфів (які мають кратні ребра).

Слід також зауважити, що коли напівейлерів граф має рівно дві вершини непарного степеня, то у всякого напівейлерового ланцюга обов'язково одна з цих вершин початкова, а друга кінцева.

Властивості гамільтонових графів.

Розглянута проблема існування замкнутого ланцюга, який проходить через кожне ребро заданого зв’язного графа G, аналогічно може бути сформульована і для вершин. Якщо у графі існує простий цикл, який проходить через усі вершини графа називається гамільтоновим.

Кількість циклів, які можна побудувати на графі називається цикломатичним числом графа.

Поняття в орієнтованому графі:

Орієнтовані маршрути на орграфі визначаються аналогічно.

Різниця тільки в тому, що початкова вершина кожної наступної дуги маршрута повинна співпадати з кінцевою вершиною попередньої дуги. Можемо сказати, що рух за маршрутом допускається тільки в направленнях, вказаних стрілками.

Маршрут, який не містить повторюваних дуг, називається шляхом, а який не містить повторюваних вершин – простим шляхом.

Замкнутий шлях називається контуром.

Ейлеров цикл – в симетричному зв`язному мультиграфі G існує тоді і тільки тоді, коли степені всіх його вершин – парні числа.

Замкнутий шлях (для орграфа) приводить в ту ж саму вершину, з якої він почався і називається контуром.

Зв`язність орієнтованих графів визначають так само, як і для неорієнтованого (не враховуючи направлення дуг).

Ізоморфізм.

Графи, які відрізняються тільки накресленням, відношення інцидентності (при відповідному позначені вершин та ребер) для них однакові. Графи, для яких зберігаються відношення інцидентності, називаються ізоморфними.

Матриця інцидентності визначає граф без петель з точністю до ізоморфізми. Графи, які мають однакові накреслення та відрізняються лише нумерацією вершин і ребер, не будучи тотожними, є ізоморфними.

Поняття дерева графа.

Зв'язний ациклічний граф називається (неорієнтованим) деревом.

Дерево завжди включає (n - 1) ребро при кількості вершин n, тобто мінімальна кількість ребер, яке необхідно для того, щоб граф був зв’язним. При добавлені у дерево ребра утворюється цикл, а при вилучені хоча б одного ребра дерево розпадається на компоненти, кожна з яких представляє собою також дерево або ізольовану вершину.

Кількість дерев, які можна побудувати на графі (для повного графа) можемо розрахувати за формулою N_t = n ^n-2.

Серед різних дерев, необхідно виділити два важливих випадки:

- послідовне дерево представляє собою простий ланцюг;

- зоряне небо в якому одна з вершин (центр) зв`язана з усіма вершинами.

Якщо дерево вилучене з будь-якого, то введемо визначення:

- гілка – це ребро графа, яке належить дереву;

- хорда – це ребро, яке не належить дереву.

Формування дерева графа:

1) вибране ребро, чергове ребро, відноситься до дерева, якщо воно не утворює цикл з вже вибраного сукупністю гілок. Ця процедура працює до того часу, доки ми не отримаємо “n – 1” гілку, які складають дерево;

2) чергове ребро знищується з графа, якщо воно утворює цикл з іншими ребрами, до того часу, поки не буде знищено q – n + 1 хорд, яке складається з доповнення ((n -1) ребер – гілок дерева).

n – вершини;

q – ребра множини E.

На рис.9 покажемо можливі типи дерев, які мають шість вершин.

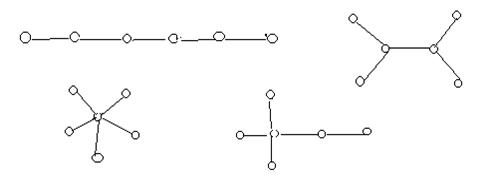
Рис. 9. Типи різних дерев, які мають шість вершин

Вище розглядались дерева як мінімальні зв’язні графи на множині n вершин. Важливе значення має і інша точка зору, коли дерева є деякі частини графа, тобто утворюються з його ребер. Будь-яка зв’язна сукупність ребер, яка не містить контурів, разом з інцидентними їм вершинами утворюють дерево графа . Якщо таке дерево є суграфом (містить усі вершини графа), то воно називається покривним деревом графа або остовним деревом.

Дерева мають важливу роль у різних прикладних задачах, коли наприклад, мова йде про зв’язки яких-небудь об’єктів мінімальним числом каналів (соціальні структури, інформаційні комунікації, кордони, дороги і т.д.) з визначеними властивостями. Дерева використовуються в якості моделей при розгляданні ієрархічних систем об’єктів.

Узагальненням поняття графа є поняття мережі. Воно вводиться відповідно до поняття мережної системи.

Мережею називають граф, кожному ребру або дузі якого поставлено у відповідність деяке число, що називається вагою ребра або дуги (наприклад: відстань, швидкість, ціну, пропускну здатність, доход, прибуток).

Мережі на практиці використовуються набагато частіше ніж графи, тому що ваги ребер чи дуг визначають функціонування об’єкта, представленого мережею. У деяких літературних джерелах поняття мережі і графа не розрізняються

Розглянемо таку задачу нехай кожному ребру графа G = (V, Е) поставлено у відповідність деяке число d_i = d(e_i), е_i Î E, i = 1, 2, ..., êЕ ê;необхідно в графі G знайти дерево, сума чисел d_i в якому найменша або найбільша. Число d_i в цьому випадку називається вагою ребра е_i, а сам граф G — таким, що має вагу.Отже, задача полягає в тому, щоб знайти дерево екстремальної ваги.

Ця задача виникає коли необхідно з'єднати задані точки деякою системою зв'язку так, щоб будь-які дві точки були зв'язані безпосередньо між собою, або через інші точки, і щоб загальна довжина ліній зв'язку була мінімальною або максимальною. Розглянемо кілька методів розв'язання цієї задачі.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Основні поняття теорії графів	\|	Алгоритми побудови дерев екстремальної ваги

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.025 сек.