Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Багатофакторна регресія

Узагальнена багатофакторна регресійна лінійна модель має вигляд:

де 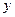– результативна змінна; 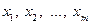– факторні змінні; 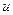– стохастична складова, 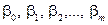– параметри моделі, а вибіркова регресійна модель:

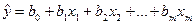де 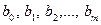– оцінки параметрів моделі.

Щоб мати явний вигляд залежності, необхідно знайти (оцінити) невідомі параметри 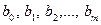цієї моделі.

Лінійною регресійною моделлю називається модель, лінійна за своїми параметрами.

Якщо лінійну багатофакторну регресійну модель записати в матричному вигляді

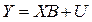
то оцінку вектора параметрів моделі можна знайти за формулою:

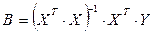
Одним із важливих припущень у багатофакторному регресійному аналізі є припущення про нормальний закон розподілу випадкової величини з нульовим математичним сподіванням та постійною дисперсією.

Можна показати, що у випадку багатофакторної регресії кожний параметр також розподіляється за нормальним законом розподілу з математичним сподіванням, яке дорівнює значенню параметра узагальненої регресії, та дисперсією, яка дорівнює дисперсії випадкової величини, помноженої на відповідний діагональний елемент оберненої матриці. Дійсне значення дисперсії випадкової величини невідоме, тому ми замінюємо його на оцінку дисперсії. Така заміна приводить до того, що кожний елемент вектора буде розподілятися вже за розподілом Ст’юдента з 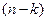ступенями вільності, що дає нам змогу обчислити 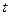-статистику для кожного параметра.

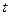-розподіл Ст’юдента дає змогу протестувати гіпотезу щодо значення кожного параметра та побудувати їх інтервали довіри, як і у випадку простої лінійної регресії.

Для перевірки оцінок параметрів багатофакторної регресії необхідно задати рівень значимості 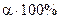, а потім побудувати 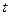-статистику для кожної оцінки 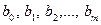окремо:

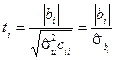
де 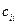– діагональний елемент матриці , 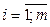. Знаменник відношення називається стандартною помилкою оцінки параметра моделі.

Незміщена оцінка дисперсії залишків:

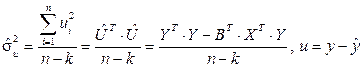
Обчислене значення критерію порівнюється з табличним при вибраному рівні значимості і 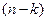ступенями свободи. Якщо 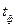< , то відповідна оцінка параметра економетричної моделі є достовірною тобто, характеризує істотній зв’язок відповідної незалежної змінної із залежною.

Для того, щоб визначити, як же знайдені оцінки параметрів багатофакторної регресії пов’язані з параметрами узагальненої регресії, потрібно побудувати інтервали довіри для параметрів.

На основі 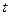-критерію і стандартної помилки можна знайти довірчі інтервали для параметрів :

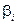з 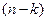ступенями свободи.

У випадку багатофакторної регресії коефіцієнт детермінації можна подати у вигляді:

, .

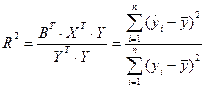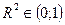Важливою властивістю коефіцієнта детермінації 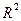є те, що він – не спадна функція від кількості факторів, які входять до моделі. Якщо кількість факторів зростає, 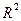також зростає і ніколи не зменшується. Тобто, якщо ми додаємо новий фактор в регресійну модель, це тільки збільшує значення 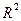, що випливає з його визначення:

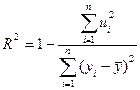
У цьому виразі знаменник не залежить від кількості факторів, тоді як чисельник, навпаки, залежить. Інтуїтивно зрозуміло, що якщо кількість факторів зростає, сума квадратів відхилень спадає (або принаймні не зростає). Якщо ми будемо порівнювати дві регресійні моделі з однаковою залежною змінною, але різною кількістю факторів 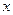, то, звичайно, віддамо перевагу тій, яка має більше значення .

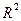Якщо ми хочемо порівняти значення коефіцієнтів детермінації в різних моделях, ми повинні взяти до уваги кількість факторів 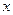у моделях. Для цього вводиться оцінений або скоригований за Тейлом коефіцієнт детермінації, який має вигляд:

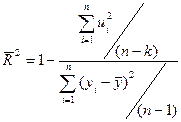
де 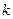- кількість параметрів регресійної моделі, включаючи перетин.

Можна показати, що 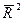та 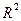пов’язані між собою такою ззалежністю:

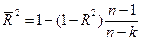
З останнього виразу зразу ж випливає: якщо 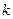> 1, то 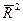< 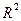. Крім того, якщо кількість факторів 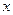зростає, оцінений коефіцієнт детермінації зменшується порівняно з не оціненим коефіцієнтом. Оцінений коефіцієнт детермінації може бути і від’ємним на відміну від 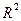, який має завжди додатне значення. Крім того, коли 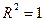, оцінений коефіцієнт кореляції 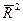також дорівнює одиниці. Коли 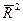прямує до від’ємної величини, 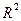прямує до нуля.

Для перевірки адекватності багатофакторної регресійної моделі, як і у випадку простої лінійної моделі, використовується 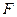-критерій Фішера.

При цьому нуль-гіпотеза узагальнюється і має вигляд:

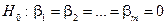проти альтернативної гіпотези 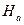– хоча б одне значення 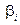відмінне від нуля.

Якщо нуль-гіпотеза неправильна, то тоді правильна гіпотеза 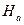, тобто не всі параметри незначно відрізняються від нуля, що дає підставу вважати, що побудована регресійна модель відповідає дійсності, тобто адекватна.

Розраховується 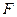-статистика Фішера з 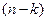та 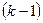ступенями вільності:

В цій формулі 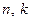– кількість спостережень та кількість параметрів відповідно.

Фактичне значення даного критерію порівнюється з критичним для заданого рівня значимості 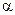. Якщо 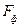> 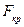, то зі ймовірністю 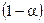ми стверджуємо, що побудована нами модель є адекватною. Або навпаки, якщо < .

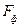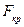Якщо побудована модель виявилася адекватною, то ми можемо використовувати її для знаходження прогнозних значень результативної змінної.

Припустимо, нам відомі значення факторів в період 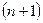, тоді ми можемо отримати прогнозне значення 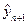за моделлю:

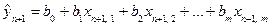
Інтервальні прогнози результативної змінної з 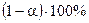рівнем довіри для побудованої моделі обчислюються за формулами:

для індивідуального значення залежної змінної:

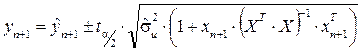
для математичного сподівання:

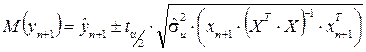
<== попередня сторінка	\|	наступна сторінка ==>
Парна регресія	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.