• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Задачі до контрольної роботи №1

1. Знайти відсотковий уміст ізотопу ¹³₆С в природному вуглеці, який складається із ізотопів ¹²₆С та ¹³₆С. Атомна маса природного вуглецю М(С)=12.01115, а ізотопна М(¹³₆С)=13,03354 а. о. м.

Вказівка

Використати визначення атомної одиниці маси (а.о.м.), тобто М(¹²₆С)=12.0. Таким чином

хМ(¹³₆С)+(1-х)М(¹²₆С)=М(С). Звідки дістанемо: х=0,011=1,1%.

2. Порівняти гравітаційну, кулонівську та ядерну енергії двох взаємодіючих протонів на відстані r=1 фермі. (G₀=6,67´10^-8 см³´г´с, m_p=1,67´10^{-24 г, е=4,8}´10^-10СГСq). Енергію ядерної взаємодії вважати такою, що дорівнює середній енергії зв’язку одного нуклона в ядрі.

Вказівка

Використати закон всесвітнього тяжіння E_грав=G₀·m_p·m_p/r, де G₀–гравітаційна стала, m_p-маса протона, r-відстань між протонами, а також закон Кулона E_кул=e·e/r, де е-заряд протона. Після обчислення маємо: E_грав=10^-43еВ, E_кул=1,2 МеВ, E_ядер=8 МеВ.

3. Довести, що в протоні не може міститись електрон як структурна частинка.

Вказівка

Скористаємось принципом невизначеностей Гайзенберга Δp_x·Δx≥h/2π, де h-стала Планка (h=6,63·10^-27ерг/с). Вважаючи невизначеність в координаті рівною розміру протона ·Δx=1,3 ф, аневизначеність в імпульсі рівною самому імпульсу електрона Δp_x=p_е, матимемо p_е≥h/(2πΔx). Для обчислення енергії необхідно скористуватись релятивіським зв’язком між енергією і імпульсом електрона E_e=p_ec, де с - швидкість світла. Кінцевий результат: E_e=150 МеВ. Ця енергія значно перевищує кулонівську енергію взаємного притягання електрона і протона, тому електрон покине протон.

4. Скільки потрібно часу нейтрону, який має енергію K_n=20МэВ, щоб перетнути ядро ²³₁₁Na? Маса нейтрона m_n=1,67´10^-24г. Що використовується як природна одиниця часу тривалості ядерних процесів?

Вказівка

Ядро вважати сферичним з радіусом R_я=r₀A^1/3, де r₀ –параметр який дорівнює 1,3x10^-13см, а А-масове число. Швидкість нейтрона визначимо із кінетичної енергії. Тоді час t, необхідний для перетину відстані 2R_я, буде дорівнювати 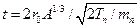, звідки t≈10^-22c.

5. Оцінити густину ядерної матерії (ρ_я), концентрацію нуклонів (N_нук) та об’ємну густину електричного заряду в ядрі (ρ_зар).

Вказівка

Для визначення зазначених характеристик, об’єм ядра визначаємо через його радіус V_я=4/3πR_я³, де R_я=r₀A^1/3, а r₀=1,3x10^-13см. Масу ядра з достатньою точністю можна вважати М_я=Аm_н, де m_н- маса нуклона m_н=1,67´10^{-24 г.} Таким чином, ρ_я=3m_н/4πr₀³, N_нук=3/4πr₀³. Для визначення об’ємної густини електричного заряду в ядрі зробимо припущення, що Z=A/2, тоді ρ_зар=3е/2πr₀³ (елементарний заряд е=1,6х10¹⁹ Кл).

6. Визначити густину ядерної матерії та радіус Землі, якщо б вона зі своєю реальною масою (6·10²⁴ кг) мала густину ядерної матерії. Масу нуклону взяти такою, що дорівнює m_н=1,67´10^{-27 кг.}

Вказівка

Вважаючи форму атомного ядра сферичною, визначимо густину ядерної матерії

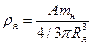(1)

Де m_н-масануклона, А-масове число, R_я-радіус ядра, причому, R_я=r₀A^1/3, а r₀=1,3x10^-13см. Підставляючи вираз для радіусу ядра в формулу (1)дістанемо густину ядерної матерії ρ_я=3m_н/4πr₀³=1,82х10¹⁴ г/см³.

Маса Землі М_з=4/3πR_з³ρ_з, де ρ_з - її густина (за умовою задачі вона повинна дорівнювати густині ядерної матерії: ρ_з=ρ_я), R_з - радіус Землі.

Шуканий радіус Землі при заданих умовах ≈200 м.

7. Визначити заряд радіоактивного ядра, для якого енергія К_a - випромінювання збудженого атома складає E_Kα=26 КеВ.

Вказівка

Використати закон Мозлі, який встановлює зв’язок між зарядом ядра (Z) і енергією характеристичного К_aвипромінювання 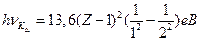, де hν=E_Kα.

Відповідь Z=49 (Индий).

8. Ядро урану ²³⁸₉₂U поділяється на два уламки приблизно однакової маси, які розташовані в середині Періодичної таблиці елементів. Користуючись кривою залежності питомої енергії зв’язку від масового числа оцініть енергію, яка вивільнюється в цій реакції.

Вказівка

Згідно закону збереження числа нуклонів, після розподілу ядра урану ²³⁸₉₂U утворюються два осколки з масовим числом ~117 та декілька вільних нейтронів. Із емпіричного графіка залежності питомої енергії зв’язку (ε) від масового числа знайдемо, що для ²³⁸₉₂U величина ε(U) =7.6 МеВ, а для двох уламків - ε(А=170)=8.5 МеВ. Таким чином при розподілі вивільнюється енергія ΔЕ=214 МеВ.

9. Скільки компонентів надтонкої структури мають основні терми атомів тритію ₁³Н₂(²S_1/2) і берилію ₄⁹Ве(¹S₀)? В дужках указані основні терми електронних оболонок атомів.

Вказівка

Скористатись правилами визначення кількості компонентів векторної суми квантово-механічних векторів: 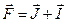, де 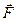- вектор повного моменту атома, 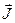- вектор повного моменту електронної оболонки, а 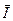- вектор спіну ядра. Для квантових чисел відповідних векторів маємо співвідношення |J-I| ≤ F ≤ (J-I). Кількість компонентів надтонкої структури (значень N_F) буде визначатись меншим квантовим числом, тобто: якщо J<I то N_F=(2J+1), а якщо I<J то N_F=(2I+1).

Квантове число повного моменту атома J знаходимо із терму атома. Для визначення квантового числа спіну ядра I скористуємось адитивною моделлю Шмідта для підрахунку спіну ядра, яке складається із протонів і нейтронів. Таким чином, основний терм атома тритію матиме дві компоненти, берилію - одну компоненту.

10. Для ядер ¹⁶₈О і ²³⁹₉₄Ри порівняйте енергії об’ємну, поверхневу та кулонівського відштовхування, якщо сталі в формулі Вейтзеккера дорівнюють α=14МеВ; β=13МеВ; γ=0.75МеВ.

Вказівка

Використати напівемпіричну формулу Вейтзеккера для обчислення енергії зв’язку ядра з зарядом Z та масовим числом А

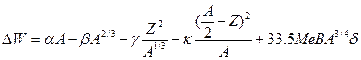
де E_об=αA - об’ємна енергія, E_пов= 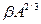- поверхнева енергія, E_кул= 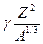- енергія кулонівського відштовхування.

11. Визначити стабільний ізобар ядер з масовим числом А=31.

Вказівка

Стабільним ізобарним ядром буде ядро з найбільшою енергією зв’язку. Дослідивши напівемпіричну формулу Вейтзеккера для обчислення енергії зв’язку ядра на екстремум (див. попередню задачу), вважаючи Z змінним а A=const. дістанемо заряд ядра стабільного ізобара 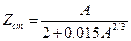. Підставляючи значення А, маємо 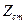=15 ( ).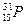

12. Визначити електричну потужність атомної електростанції, якщо витрата ізотопу 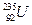складає 235 кг на рік при ККД=31%.

Вказівка

Звісно, що при поділі одного ядра 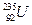вивільнюється енергія біля ε=210МеВ. Повна енергія , яка вивільнюється при поділі m=235 кг 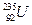за рік (t=3,1х10⁷ с) дорівнює добутку кількості ядер, які поділилися (n_яд), на енергію поділу: E_пов=n_ядε. Кількість ядер вирахуємо використовуючи число Авагадро N_A=6.02x10²³ атомів/моль. Електрична потужність (P) атомної електростанції визначається 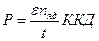. Відповідь: 200 МВт.

Контрольна робота з першого модуля включатиме 2 теоретичних питання з лекційного матеріалу, одне питання з самостійної роботи, та дві задачі.

Переглядів: 1573