• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Знаходження похідних.

Аналогічно до інших найбільш важливих математичних операцій, в Mathcad передбачено чисельне і символьне диференціювання. Практично в 99% випадків можна знайти аналітичне значення похідної. Чисельне знаходження похідних потрібне лише для ряду специфічних задач. Також слід зауважити, що чисельне диференціювання при великих степенях дає велику похибку.

Для операцій диференціювання та інтегрування ми будемо користуватися панеллю Calculus (Обчислення) Математичної панелі.

7. Знаходження похідної першого порядку.

Для знаходження похідної першого порядку в Mathcad використовують оператор Derivative з панелі Calculus. Оператор Derivativeмає два маркера, принцип заповнення їх відповідає математичним стандартам: в верхній вводимо функцію, в нижній – змінну, по якій відбувається диференціювання.

Якщо вираз, який ми диференціюємо складається з добутків, або різниць, його треба взяти в дужки. В якості оператора виводу результату використовуємо або → або = в залежності від того, символьний чи чисельний результат нам потрібен.

При символьному диференціюванні можна оперувати функціями декількох змінних та функціями з параметрами. Також оператор диференціювання може можна поєднувати із будь-яким іншим обчислювальним або символьним оператором.

Розглянемо приклад:

З прикладу1 видно, що знайдено похідну лише від першої частини виразу.

З прикладу2 видно, що знайдено похідну 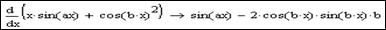від усього виразу, що в дужках.

Також можна знайти похідну, спочатку задавши функцію, а потім ввівши її ім’я у відповідні маркери диференціювання.

8. Знаходження похідних вищих порядків.

Для знаходження похідних вищих порядків використовують оператор Nth Derivative панелі Calculus. Оператор має в собі чотири маркера. Вони заповнюються повністю у відповідності до правил прийнятих в математиці. Достатньо ввести показник степеня в один з маркерів, як він відобразиться в другому автоматично.

Порядок похідної обов’язково повинен бути числом. Аналітичне знаходження похідної з неявно заданим порядком – неможливий. А ось функція, від якої ми знаходимо похідну, може бути як завгодно складною. Також функція може містити в собі параметри.

Приклад:

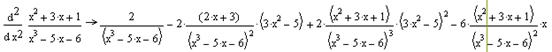
Із приклада видно, що символьний процесор шукаючи похідну не спрощує вираз. Тому, для того, щоб отримати відповідь у спрощеному вигляді, потрібно застосувати оператор Simplify.

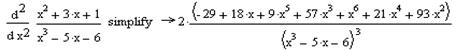
Аналогічно звичайним похідним, похідні вищих порядків також можна знаходити як аналітично так і чисельно. Однак, слід зауважити, що при чисельному знаходженні, порядок похідної не може бути вище ніж 5. (При спробі задання вищого порядку ніж 5, програма видасть повідомлення про помилку). Це пов’язано з тим, що при застосуванні чисельного метода накопичується велика похибка. Тому в таких випадках завжди варто використовувати символьний процесор.

9. Знаходження похідної від функції декількох змінних.

Для того, щоб знайти похідну від функції декількох змінних (Частинну похідну), потрібно спочатку перетворити оператор Derivative.Для цього:

- вводимо оператор Derivative.

- Викликаємо на ньому контекстне меню.

- Вибираємо пункт: - View Derivative as (зобразити похідну як).

- Вибираємо пункт Partial Derivative. (частинна похідна)

Якщо буде потрібно повернутися до звичайного вигляду оператора, дії виконати послідовно навпаки. Так само можна обчислювати похідні декількох функцій вищих порядків.

Приклад: Знайти всі частинні похідні для функції f(x,y,z)=x²*e^x+z-y³

Розв’язання:

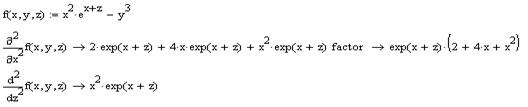
10. Знаходження інтегралів.

Знаходження визначених інтегралів в Mathcad може бути як чисельним так і символьним. Обчислення невизначених – тільки символьним. У будь-якому випадку, спочатку потрібно намагатися отримати аналітичний результат, я лише у випадку невдачі – чисельний.

Також в Mathcad можна обчислювати подвійні, потрійні а також невласні інтеграли.

На практиці 99% задач на знаходження інтегралів розв’язується правильно. У яких випадках програма не може виконати завдання:

- Якщо функція, у тому вигляді, в якому ви її задали, не підпадає під жодну формулу інтегрування, що міститься в довіднику програми. У цьому випадку потрібно виконати певну заміну або спрощення перед інтегруванням.

- Якщо результат є надто великим, не піддається спрощенню і його неможливо вивести не екран. У цьому випадку потрібно розбити початкову функцію на декілька частин і брати інтеграл від кожної з них.

- Якщо функція, яку потрібно про інтегрувати, містить в собі рекурентні співвідношення, ряди та їх добутки.

11. Знаходження невизначеного інтегралу.

Для знаходження невизначеного інтегралу в Mathcad існує спеціальний оператор Indefinite Integral (Невизначений інтеграл) панелі Calculus (Обчислювальні). Його зображення на кнопці цілком відповідає зображенню, прийнятому в математиці. Оператор невизначеного інтеграла має два маркера. Заповнюємо їх відповідно до правил математики: в лівий маркер вводимо функцію, в правий – змінну, по якій проводимо інтегрування. В кінці ставимо оператор символьного виводу "→".

Приклад: Знайти невизначений інтеграл.

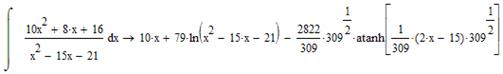
Часто буває, що результат інтегрування виявляється занадто громіздким і його бажано було б спростити. Для цього використовують оператори панелі Символьні: Simplify для простого спрощення, Collect – для зведення подібних доданків, Expand – для розкладення степенів та Factor – для приведення до спільного знаменника. Для того, щоб задіяти потрібний символьний оператор, потрібно виділити вираз інтеграла і натиснути відповідну кнопку панелі Symbolic. Для спрощення результату інтегрування можна застосовувати одразу по кілька операторів.

Слід зауважити, що в кінцевій відповіді Mathcad не додає константу С. Тому, якщо це є важливим, в оформленні потрібно дописати +С самостійно.

1. Аналітичне знаходження визначеного інтегралу.

Для знаходження визначеного інтегралу в Mathcad існує оператор Definite Integral (Визначений інтеграл) панелі Calculus. Оператор Definite Integral має вигляд такий самий як і в математиці, містить в собі чотири маркера, які заповнюються відповідно правилам інтегрування. Знаходити чисельний результат варто лише в тому випадку, коли неможливо знайти аналітичний. Якщо відповідь вийде надто громіздкою, слід користуватися операторами, що використовуються для спрощення.

Приклад1 стандартний і приклад2 для знаходження інтегралу з неявно заданими межами:

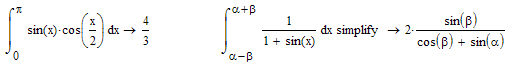
У випадку знаходження інтегралів з неявно заданими межами слід використовувати оператор Simplify для отримання простого варіанту відповіді. Також слід пам’ятати, що всі функції і числа Mathcad розглядає в комплексній області, тому неправильно задавши межі можна отримати комплексне значення. Якщо потрібно отримати результат інтегрування у вигляді числа, достатньо поставити знак "=" після аналітичної відповіді, або застосувати оператор Float із потрібною точністю.

1. Знаходження кратних інтегралів.

Для того, щоб знайти кратний інтеграл потрібно виконати таку послідовність дій:

1. Ввести з панелі Calculusпотрібний вам оператор інтегрування.
2. Поставити курсор в маркер підінтегральної функції і ввести другий оператор інтегрування. Для обчислення потрійного інтеграла, потрібно виконати цю операцію два рази.
3. В маркері останнього з заданих операторів прописати функцію, яку потрібно проінтегрувати.
4. Заповнити маркери диференціалів у тому порядку, в якому повинно відбуватися інтегрування.
5. Якщо знаходиться визначений інтеграл – заповнюємо маркери відповідних меж.

Приклад: Обчислити значення кратного інтегралу:

Слід пам’ятати, що і у випадку знаходження кратних інтегралів, чисельний метод застосовується лише тоді, коли символьний процесор не може виконати завдання.

Переглядів: 3227