• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Точки перегину.

Лист контролю.

Модуль №3.

1. Степінь з довільними показниками.

2. Основні показникові тотожності.

3. Означення логарифма. Основна логарифмічна тотожність.

4. Властивості логарифмів.

5. Степенева функція, її властивості та графіки.

6. Показникові функція, її властивості та графіки.

7. Логарифмічна функція, її властивості та графіки.

Література:

1. О.М. Афанасьєва «Математика». 2001р.

2. О.М. Афанасьєва «Дидактичні матеріали з математики». 2001р.

3. М.І. Шкіль «Алгебра і початки аналізу» 10 – 11 кл. 1995р.

4. Н.В. Богомолов «Практические занятия по математике» 1990р.

Тема 4: Похідна та її застосування.

1. Задачі, які приводять до поняття похідної.

2. Похідна. Механічний та геометричний зміст похідної.

3. Формули диференціювання.

4. Друга похідна та її фізичний зміст.

5. Застосування похідної.

1. Зростання, спадання функції.

2. Екстремуми функції.

4. Друге правило дослідження функції на екстремум.

5. Асимптоти кривої.

6. Загальна схема дослідження функції і побутова графіка.

7. Рівняння дотичної.

Найбільше і найменше значення функції на відрізку.

1. Задачі, які приводять до поняття похідної.

а) Задача про миттєву швидкість.

змінна.

?

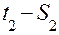
Нехай а

миттєва.

миттєва.

б) Задача про дотичну до кривої.

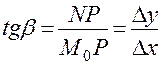
Нехай 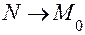, рухаючись по кривій. Тоді січнадо дотичної, а

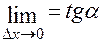
2. Похідна. Механічний та геометричний зміст похідної.

Означення похідної.

Границя відношення просторі 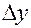до приросту аргументу , якщо приріст аргументу прямує до нуля, називається функції 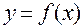в точці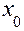і позначається .

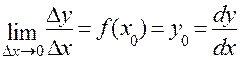Операція знаходження похідної називається диференціюванням функції.

Фізичний зміст похідної:

Похідна від шляху по часу дорівнює 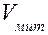в заданий момент часу .

Геометричний зміст похідної:

Похідна функції в точці 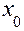дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції в точці з абсцисою .

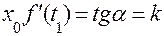Загальний метод знаходження похідної.

Похідна від функції знаходиться по слідуючих кроках:

1) Знаходимо в точці 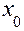приріст функції;

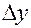2) Знаходимо - відношення приросту функції до приросту аргументу;

3) Знаходимо границю цього відношення при умові, що .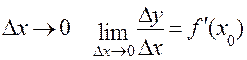

3. Формули диференціювання.

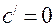
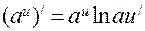
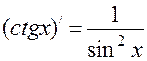
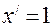
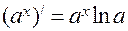
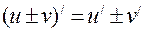
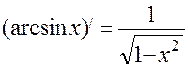
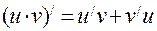
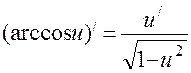
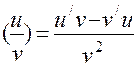
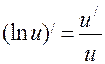
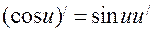
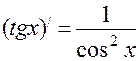
4. Друга похідна та її фізичний зміст.

Похідна від першої похідної називається другою похідною і позначається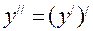

, ,

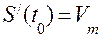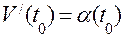Друга похідна від 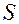по дорівнює прискоренню в заданий момент часу .

5. Застосування похідної.

1. Зростання та спадання функції.

Теорема про необхідні та достатні умови зростання та спадання функції на проміжку:

Якщо, функція 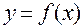диференційована на 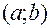і , для , то функція на цьому проміжку зростає, а якщо 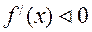для , то функція на цьому проміжку спадає.

Схема дослідження функції на монотонність:

1) Знаходимо ;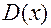

2) Знаходимо критичні точки (точки, в яких похідна дорівнює нулю, або не існує);

3) Критичні точки ділять 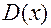на проміжки монотонності;

З кожного проміжку виберемо довільну точку і підставимо її в похідну, якщо , то функція зростає на цьому проміжку, якщо 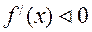, то функція спадає на цьому проміжку.

2. Екстремуми функції.

Основні означення:

Точка 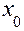називається точкою максимуму функції 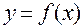, якщо для 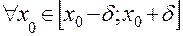виконується умова.

Значення функції в точці максимуму називається максимумом функції і позначається .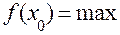

Точка 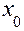називається точкою мінімуму функції 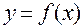, якщо для 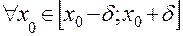виконується умова .

Значення функції в точці мінімуму називається мінімумом функції і позначається .

Мах і тіn функції називається екстремумом функції.

Необхідна умова існування екстремуму:

Теорема Ферма:

Якщо 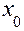точка екстремуму функції 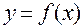і функція в цій точці має похідну, то .

Достатня умов аекстремуму.

Теорема Роля.

Якщо при переході через критичну точку 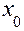похідна неперервної функції змінює знак, то функція в цій точці має екстремум, якщо:

1) з "+" на "-", то 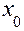- точка максимума;

2) з "-" на "+", то 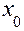- точка мінімума.

Схема дослідження функції на екстремум:

1. Знаходимо критичні точки першого роду.

2. Розміщуємо критичні точки в порядку зростання. підставляємо в похідну любе число менше 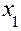, потім більше 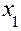, але менше 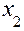. Якщо при цьому знак похідної змінюється з "+" на "-" , то функція при 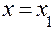має максимум, якщо з "-" на "+", то функція при 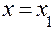має мінімум.

3. Обчислюємо 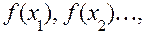тобто знаходимо максимальне значення функції.

Читайте також:

1. Алгебраїчний спосіб визначення точки беззбитковості
2. Аналіз точки беззбитковості
3. Видалення характерної точки
4. Визначення точки
5. Визначення точки беззбитковості
6. Визначення точки беззбитковості.
7. Визначення. Точки максимуму й мінімуму функції називаються точками екстремуму.
8. Відстань від точки до площини і від точки до прямої на площині
9. Диференціальні рівняння руху вільної матеріальної точки
10. Енергетичні рівні напівпровідникової квантової точки
11. З точки зору динамічного підходу механізм соціального конфлікту проходить зазвичай наступні стадії протікання конфлікту.
12. З точки зору цілей, які відстоюють протидіючі сторони конфлікту розподіляються на особисті, групові, суспільні.

Переглядів: 1802