Координація, координаційні число, сфера, поліедр

Координація– оточення того чи іншого атому (або іншої структурної одиниці), число сусідів, їх сорти, відстані між ними.

Координаційне число– число найближчих сусідніх атомів або іонів одного сорту, що знаходяться на одній відстані від атому або іону, прийнятого за центральний.

Координаційні числа (к.ч.) у структурах кристалів визначаються природою сил міжатомної взаємодії (тип зв’язку, температура, тиск) між матеріальними частками.

Структури металів проявляють тенденцію до високої координації, тобто, к.ч. = 12 або 8. Той самий принцип властивий і іонним кристалам, в яких кожен іон «прагне» оточити себе максимально більшим числом протилежно заряджених іонів. але з дотриманням принципу електричної нейтральності.

Координаційне число залежить, також, від відносних розмірів центрального іону та його сусідів.

Найменше значення к.ч. мають неметалічні речовини (сірка, фосфор та інш.). Застаріла назва цих речовин – металоїд. Їх к.ч. 3 – 4.

У найпростіших структурах металів і іонних сполук найближчі сусіди, оточуючі центральний атом (іон), розташовуються в симетрично рівних за відстанню позиціях. Число сусідів у такій просторовій позиції є к.ч. першої координаційної сфери.

Наступна за віддаленістю просторова конструкція упорядкованих сусідів складає другу координаційну сферу і так далі.

У складних і низько симетричних структурах відстань до найближчих сусідів може бути не однаковою. Але якщо відстань до наступної сфери суттєво більша, ніж відхилення в аналізованій, то зазначену сукупність сусідів включають до однієї координаційної сфери.

Якщо відстань до першої і другої координаційних сфер близькі, тоді їх розподіл здійснюють умовно із зазначенням обох к.ч., наприклад – 8 + 6 і т.п.

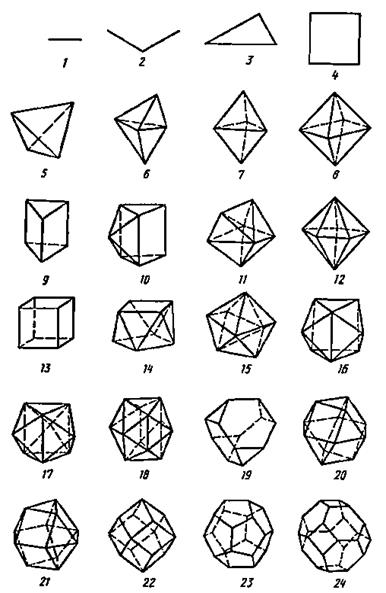
Координаційний поліедр– координаційний багатогранник (поліедр), представляє собою геометричну фігуру, обмежену пласкими гранями, всі вершини якої зайняті атомами (іонами) одного сорту (рис. 2.4).

Рисунок 2.4 – Типи координаційних поліедрів

Будується методом з’єднання центрів найближчих атомів (іонів) першої координаційної сфери.

На рисунку 2.4 представлені координаційні поліедри (к.ч.): 1 – гантель (1); 2 – куток (2); 3 – трикутник (3); 4 – квадрат (4); 5 – тетраедр (4); 6 – тетрагональна піраміда (5); 7 – тригональна діпіраміда (5); 8 – октаедр (6); 9 – тригональна призма (6); 10 – одношапочна тригональна призма (7); 11 – семивершинник (7); 12 – пентагональна діпіраміда (7); 13 – куб (8); 14 – квадратна антипризма (8); 15 – тригональний додекаедр (8); 16 – двошапочна призма (8); 17 – трьохшапочна тригональна призма (9);18 – ікосаедр (12); 19 – притуплений тетраедр (12); 20 – кубооктаедр (12); 21 – гексагональний кубооктаедр (12); 22 – ромбододекаедр (14); 23 – пентагондодекаедр (20); 24 – притуплений октаедр (24).

У координаційного поліедра число вершин дорівнює координаційному числу. Відстань від вершини до центрального атому (іону) дорівнює міжатомній відстані у відповідній координаційній сфері. Ребра поліедра – відстань між найближчими сусідами центрального атому. Рисунок 2.4 свідчить про те, що одному і тому ж к.ч. можуть відповідати різні координаційні поліедри.

<== попередня сторінка	\|	наступна сторінка ==>
Атомні та іонні радіуси	\|	Приклад практичного застосування методу симетрії для аналізу мікроструктур промислових сплавів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.