
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Многокутники.
Многокутникомназивається проста замкнена ламана. Наприклад, многокутником А1А2…Аn називається лінія, яку отримують при послідовному сполученні n різних точок А1, А2, …, Аn відрізками так, щоб кожна точка була сполучена з наступною, а остання з першою (рис.1.12). Розрізняють многокутники плоскі й не плоскі. Плоский многокутник – частина площини, обмежена многокутником.
 |
Також будь-який многокутник може бути опуклим або не опуклим. Многокутник опуклий, якщо він лежить в одній півплощині відносно кожної прямої, що проходить через дві його сусідні вершини (рис.1.12, б, г, д).
 Многокутники називають рівними, якщо вони при накладанні суміщаються. Для опуклого n – кутника сума внутрішніх кутів дорівнює
Многокутники називають рівними, якщо вони при накладанні суміщаються. Для опуклого n – кутника сума внутрішніх кутів дорівнює 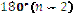 , а кількість діагоналей будь-якого n – кутника дорівнює
, а кількість діагоналей будь-якого n – кутника дорівнює 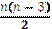 . Якщо всі сторони опуклого многокутника рівні між собою і всі кути теж рівні між собою, то його називають правильним(рис. 1.12,д). Якщо всі вершини многокутника лежать на деякому колі, то він називається вписанимв це коло. Якщо сторони многокутника дотикаються до деякого кола, то він називається описаним навколо кола (рис.1.13). За кількістю сторін n – кутника, йому дають назву. Наприклад, трикутник (n = 3), чотирикутник (n = 4), п’ятикутник (n = 5) і т.д.
. Якщо всі сторони опуклого многокутника рівні між собою і всі кути теж рівні між собою, то його називають правильним(рис. 1.12,д). Якщо всі вершини многокутника лежать на деякому колі, то він називається вписанимв це коло. Якщо сторони многокутника дотикаються до деякого кола, то він називається описаним навколо кола (рис.1.13). За кількістю сторін n – кутника, йому дають назву. Наприклад, трикутник (n = 3), чотирикутник (n = 4), п’ятикутник (n = 5) і т.д.
Як побудувати правильний n – кутник?

Якщо коло поділити на n рівних частин і точки послідовно сполучити відрізками, то дістанемо правильний n – кутник, вписаний у коло (рис. 1.14).
Якщо коло поділити на n рівних частин і через точки поділу провести дотичні до кола, то відрізки цих дотичних утворять правильний n – кутник описаний навколо кола (рис. 1.15).

Навколо кожного правильного многокутника можна описати коло або у кожний правильний многокутник можна вписати коло.
У правильному многокутнику центри описаного і вписаного кіл співпадають. Спільний центр описаного і вписаного кіл називається центром правильного многокутника. Радіус вписаного кола називають апофемою правильного многокутника.
Кут, утворений двома радіусами, проведеними у суміжні вершини правильного многокутника, називається його центральним кутом. Усі центральні кути правильного многокутника між собою рівні, вони дорівнюють 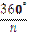 , де n – кількість сторін (кутів) многокутника.
, де n – кількість сторін (кутів) многокутника.
У правильному n – кутнику, як і в довільному n – кутнику, сума всіх кутів (внутрішніх) становить 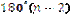 . Тому кожний його кут визначається за формулою
. Тому кожний його кут визначається за формулою 
Коло, вписане у правильний многокутник, дотикається до його сторін в їх серединах. Центр кола, вписаного у правильний многокутник, є точкою перетину серединних перпендикулярів до його сторін (рис. 1.15).
Якщо сторона правильного многокутника дорівнює а, радіус, вписаного у нього кола, – r, а радіус описаного навколо нього кола –  , то між ними існує взаємозв’язок, що виражається формулами:
, то між ними існує взаємозв’язок, що виражається формулами:
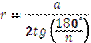 ,
,  .
.
Якщо n = 3(правильний трикутник), то: 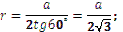
 .
.
Якщо n = 4(правильний чотирикутник), то: 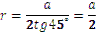 ;
;  .
.
Якщо n = 6(правильний шестикутник), то:  ;
; 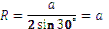 .
.
 |
Найпростішим многокутником є трикутник. У будь-який трикутник можна вписати коло, при чому тільки одне (рис.1.16,б). На рис.1.16,б зображено коло з центром О, вписане в трикутник АВС,
 – його радіус. Центр кола, вписаного в трикутник, є точкою перетину його бісектрис і знаходиться всередині площини цього трикутника. Оскільки площу трикутника знаходять за формулою:
– його радіус. Центр кола, вписаного в трикутник, є точкою перетину його бісектрис і знаходиться всередині площини цього трикутника. Оскільки площу трикутника знаходять за формулою: 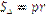 , де р – півпериметр трикутника, то звідси
, де р – півпериметр трикутника, то звідси 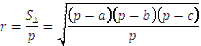 , де а, b, с – сторони трикутника. Центр кола, вписаного в трикутник, рівновіддалений від його сторін.
, де а, b, с – сторони трикутника. Центр кола, вписаного в трикутник, рівновіддалений від його сторін.
Чи можна у будь-який чотирикутник вписати коло?
Відповідь. Не можна. У чотирикутник можна вписати коло, при умові, що суми довжин його протилежних сторін рівні.
Навколо довільного трикутника можна описати коло, причому тільки одне (рис. 1.16,а). Центр кола, описаного навколо трикутника, є точкою перетину серединних перпендикулярів проведених до його сторін. Центр кола О, описаного навколо трикутника АВС, рівновіддалений від його вершин.
На рис. 1.16, а зображено коло з центром О, описане навколо трикутника АВС,  – його радіус. Якщо радіус описаного кола R, сторони трикутника, вписаного в коло, а, b і с, то
– його радіус. Якщо радіус описаного кола R, сторони трикутника, вписаного в коло, а, b і с, то  , де p – півпериметр трикутника.
, де p – півпериметр трикутника.
Чи можна описати коло навколо довільного чотирикутника?
 Відповідь. Не можна. Навколо чотирикутника можна описати коло тоді, коли суми протилежних кутів рівні
Відповідь. Не можна. Навколо чотирикутника можна описати коло тоді, коли суми протилежних кутів рівні 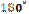 .
.
Трикутник та його елементи.
Трикутникомназивається фігура, яка складається із трьох точок, що не лежать на одній прямій, і трьох відрізків, що попарно сполучають ці точки. Розглянемо 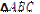 (рис. 1.17), в якому виділяють 6 основних елементів: 3 внутрішні кути
(рис. 1.17), в якому виділяють 6 основних елементів: 3 внутрішні кути  і 3 відповідно протилежні їм сторони а, b, c.
і 3 відповідно протилежні їм сторони а, b, c.
Трикутник називається тупокутним, прямокутним або гострокутним, якщо його найбільший внутрішній кут відповідно більший, дорівнює або менший від 90°.
Трикутник називається рівнобедреним,якщо в нього дві сторони рівні (бічні сторони). Основою рівнобедреного трикутника є та сторона, яка не дорівнює жодній з інших двох рівних сторін.
Трикутник, усі сторони якого рівні, називається рівностороннім (або правильним).
Співвідношення між сторонами і кутами трикутника (рис.1.17):
проти більшої сторони лежить більший кут і навпаки; проти рівних сторін лежать рівні кути; теорема синусів: 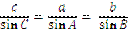 ; теорема косинусів:
; теорема косинусів:  (квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними).
(квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними).
Трикутник повністю визначається будь-якою з таких трійок своїх основних елементів: або двома сторонами і кутом між ними, або однією стороною і двома кутами, або трьома сторонами. Наприклад, △ 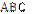 зі сторонами а, b, c можна задати так:
зі сторонами а, b, c можна задати так:
1) a, b i C; b, c i A; a, c i B;
2) a, B i C; b, A i C; c, A i B;
3) a, b і c.
Співвідношення між внутрішніми і зовнішніми кутами трикутника:будь-який зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.
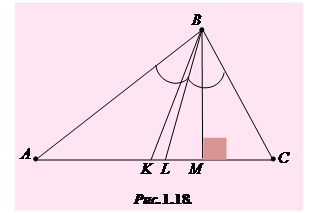 З трьох відрізків можна утворити трикутник тоді і тільки тоді, коли будь-яка його сторона менша за суму і більша за різницю двох інших його сторін. У будь-якому трикутнику можна провести три медіани, три бісектриси і три висоти.
З трьох відрізків можна утворити трикутник тоді і тільки тоді, коли будь-яка його сторона менша за суму і більша за різницю двох інших його сторін. У будь-якому трикутнику можна провести три медіани, три бісектриси і три висоти.
Властивості бісектриси кута трикутника:
Бісектриситрикутника перетинаються в одній точці, яка лежить всередині трикутника і є центром вписаного в трикутник кола. Бісектриса ділить протилежну сторону на частини, пропорційні прилеглим до неї сторонам (рис. 1.18; BL - бісектриса, AL : LС = AB : BC).
Основні властивості медіан трикутника:
1. Медіани трикутника перетинаються в одній точці, що лежить всередині трикутника.
2. Медіани трикутника точкою їхнього перетину діляться у відношенні 2 : 1 (рахуючи від вершин трикутника).
3. Медіана ділить трикутник на два трикутники, площі яких рівні (рис. 1.18; BK – медіана,).
4. Три медіани трикутника ділять трикутник на шість трикутників, площі яких рівні.
Прямі на яких лежать висоти трикутника перетинаються в одній точці – ортоцентрі трикутника, яка може міститися у внутрішній або зовнішній області трикутника. Висоти трикутника, опущені на сторони трикутника а, b, і с, позначаються ha, hb, hc відповідно. Висота трикутника ha визначається через сторони за формулою  де
де 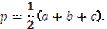
Медіана трикутника ma, проведена до сторони а, визначається через сторони трикутника формулою 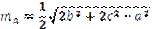 .
.
У кожному трикутнику можна побудувати три середні лінії – відрізки, які сполучають середини двох сторін трикутника. Середня лінія трикутника паралельна третій стороні трикутника та дорівнює її половині. Середня лінія трикутника відтинає від трикутника подібний трикутник. Площа відрізаного трикутника відноситься до площі основного трикутника у співвідношенні 1 : 4.
Властивості рівнобедреного трикутника: кути при основі трикутника рівні; висота, проведена до основи трикутника, є також бісектрисою і медіаною.
Властивості рівностороннього трикутника: усі кути трикутника - рівні (кожний кут дорівнює 60°); кожна з трьох висот трикутника є також бісектрисою і медіаною; центр кола, описаного навколо трикутника, збігається з центром кола, вписаного в нього.
 Прямокутний трикутник має сторону, яка лежить проти прямого кута – гіпотенузу(с) та дві сторони, які утворюють прямий кут – катети (а, b) (рис.1.19). Сторони кожного прямокутного трикутника а, b, і c (с – гіпотенуза) зв’язані між собою співвідношенням, що називається теоремою Піфагора: с2 = а2 + b2, яка читається так: квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.
Прямокутний трикутник має сторону, яка лежить проти прямого кута – гіпотенузу(с) та дві сторони, які утворюють прямий кут – катети (а, b) (рис.1.19). Сторони кожного прямокутного трикутника а, b, і c (с – гіпотенуза) зв’язані між собою співвідношенням, що називається теоремою Піфагора: с2 = а2 + b2, яка читається так: квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.
Властивості прямокутного трикутника:
1) Катет є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу: b2 = bс  с і а2 = ас
с і а2 = ас  с (рис. 1.19);
с (рис. 1.19);
2) Висота, проведена з вершини прямого кута, є середнім пропорційним між проекціями катетів на гіпотенузу: h2= bс · ас ;
3) Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи.
4) Для сторін прямокутного трикутника істинні відношення: sinÐA = 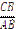 ; cosÐA =
; cosÐA =  .
.
5) Запам’ятайте!

| 
| 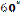
| Вказівка для кращого запам’ятовування:
1) запишіть риски дробів для кожного значення виразу sin  і cos і cos  , та знаменники, що дорівнюють 2;
2) запишіть у чисельниках числа: 1, 2, 3 (для sin , та знаменники, що дорівнюють 2;
2) запишіть у чисельниках числа: 1, 2, 3 (для sin  ), і навпаки: 3, 2, 1 (для cos ), і навпаки: 3, 2, 1 (для cos  ;
3) допишіть знак радикала до кожного чисельника дробу. Враховуючи те, що ;
3) допишіть знак радикала до кожного чисельника дробу. Враховуючи те, що  отримуємо заповнену таблицю. отримуємо заповнену таблицю.
| |
sin 
| 
| 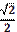
| 
| |
cos 
| 
| 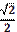
| 
|
 Опуклі чотирикутники.
Опуклі чотирикутники.
Чотирикутник, протилежні сторони якого попарно паралельні, називається паралелограмом.
Властивості паралелограма:
1) Середина діагоналі паралелограма є його центром симетрії.
2) Протилежні сторони паралелограма рівні.
3) Протилежні кути паралелограма рівні.
4) Кожна діагональ паралелограма ділить його на два рівні трикутники.
5) Діагоналі паралелограма діляться точкою перетину пополам.
6) Сума квадратів діагоналей паралелограма (d1 і d2) дорівнює сумі квадратів усіх його сторін:

Щоб довести, що деякий заданий чотирикутник є паралелограмом, треба, згідно з означенням, впевнитися у паралельності протилежних його сторін. Інколи такі міркування є громіздкими, а інколи – зайвими. Оскільки існують інші доведені ознаки, на підставі яких можна твердити, що даний чотирикутник є справді паралелограм.
Якщо у чотирикутнику справджується будь-яка з таких умов: 1) протилежні сторони попарно рівні; 2) дві протилежні сторони рівні і паралельні; 3) протилежні кути попарно рівні; 4) діагоналі, у точці перетину, поділяються пополам, то такий чотирикутник є паралелограмом.
Прямокутник – це паралелограм, в якому всі кути рівні. Оскільки сума кутів чотирикутника дорівнює  , то у прямокутника всі кути прямі. Прямокутник має всі властивості паралелограма і, окрім того, - ще таку властивість: діагоналі прямокутника рівні між собою.
, то у прямокутника всі кути прямі. Прямокутник має всі властивості паралелограма і, окрім того, - ще таку властивість: діагоналі прямокутника рівні між собою.
Для прямокутника справджується і обернена теорема про те, що коли у паралелограмі діагоналі рівні, то такий паралелограм є прямокутником. Ця теорема є ознакою прямокутника.
 Ромб –це паралелограм, в якому всі сторони рівні. Крім загальних властивостей паралелограма, ромб має ще й інші властивості, характерні лише йому. Діагоналі ромба взаємно перпендикулярні і поділяють його кути пополам. Справджується і обернена теорема, яка є ознакою ромба: якщо у паралелограмі діагоналі взаємно перпендикулярні або якщо у ньому діагоналі поділяють кути пополам, то такий паралелограм є ромб.
Ромб –це паралелограм, в якому всі сторони рівні. Крім загальних властивостей паралелограма, ромб має ще й інші властивості, характерні лише йому. Діагоналі ромба взаємно перпендикулярні і поділяють його кути пополам. Справджується і обернена теорема, яка є ознакою ромба: якщо у паралелограмі діагоналі взаємно перпендикулярні або якщо у ньому діагоналі поділяють кути пополам, то такий паралелограм є ромб.
Квадрат – це паралелограм, в якому всі кути рівні і всі сторони рівні. Отже, квадрат – це прямокутник з рівними сторонами або квадрат – це ромб з рівними кутами (прямими). Очевидно, що квадрат має всі властивості прямокутника і ромба.
 Трапеція– це чотирикутник, в якому дві сторони паралельні. Ці паралельні сторони називаються основами трапеції, дві інші сторони – бічними сторонами.
Трапеція– це чотирикутник, в якому дві сторони паралельні. Ці паралельні сторони називаються основами трапеції, дві інші сторони – бічними сторонами.
Очевидно, паралелограм є частинний випадок трапеції. Якщо бічні сторони трапеції рівні між собою, то трапеція називається рівнобічною (рис.1.21, АВ = СD).
Рівнобічна трапеція має такі властивості:
1) Кути, прилеглі до основи рівнобічної трапеції, рівні. (Справджується і обернене твердження: якщо кути, прилеглі до основи трапеції, рівні, то така трапеція рівнобічна).
2) Діагоналі рівнобічної трапеції рівні.
3) Сума протилежних кутів рівнобічної трапеції дорівнює 180°.
Відрізок, що сполучає середини бічних сторін трапеції, називається її середньою лінією (рис.1.21, MN – середня лінія, 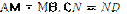 ).
).
Середня лінія трапеції паралельна її основам і дорівнює їх півсумі (рис.1.21, MN  AD, MN
AD, MN  ВС, MN =).
ВС, MN =).

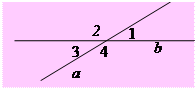
1.20°. При перетині двох прямих a і b утворилось 4 кути. Задайте кожній з умов (А – Д) можливі наслідки (1 – 5).
| А) Ð1 = Ð3; | 1) Ð3 = Ð4 = 90º; |
| ||||||||||
| Б) Ð2 + Ð3 = 180º; | 2) Ð1 = Ð2 = Ð4 = 90º; | |||||||||||
| В) Ð1 = Ð2 = 90º; | 3) Ð1 і Ð4 – суміжні; | |||||||||||
| Г) Ð2 + Ð4 = 260º; | 4) Ð1 і Ð3 – гострі; | |||||||||||
| Д) Ð3 = 90º. | 5) Ð2 і Ð4 – вертикальні. |
1.21°. Умовами (1 – 7) вказано градусну міру деяких кутів. Виберіть серед них ті, які можуть бути суміжними.
| 1) 18º; | 2) 72º; | 3) 128º; | 4) 62º; | 5) 28º; | 6) 108º; | 7) 38º. | |||||
| А) 1 і 2; | Б) 2 і 6; | В) 3 і 4; | Г) 1 і 7; | Д) 2 і 5. | |||||||
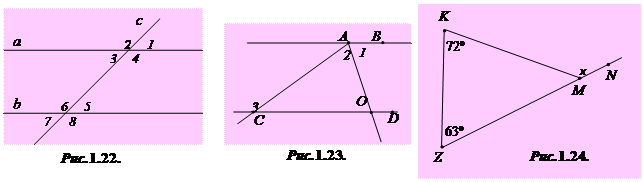 |
1.22°. Виберіть правильний висновок, користуючись даними рисунка 1.22 , якщо відомо, що Ð1 = Ð7.
| А) a || b; | Б) a 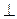 b; b;
| В) a  b. b.
|
1.23°°. Знайдіть градусну міру Ð3 (рис. 1.23), якщо CD || AB, Ð1 = Ð2 і Ð2 = 72º.
| А) 72º; | Б) 144º; | В) 108º; | Г) 36º; | Д) 124º. |
1.24°. Знайдіть градусну міру зовнішнього кута KMN трикутника KMZ (рис. 1.24).
| А) 135º; | Б) 125º; | В) 108º; | Г) 117º; | Д) 45º. |





 1.25°. Знайдіть градусну міру кута між бісектрисою кута при вершині
1.25°. Знайдіть градусну міру кута між бісектрисою кута при вершині
рівнобедреного трикутника та його бічною стороною, якщо кути трикутника
ABC відносяться як 3 : 4 : 3.
| А) 18º; | Б) 36º; | В) 72º; | Г) 60º; | Д) 30º. |
 1.26°. Визначте, користуючись даними рисунка1.25 правильні рівності.
1.26°. Визначте, користуючись даними рисунка1.25 правильні рівності.
| А) ∆ABO =∆OCD; | Г) ÐAOB =ÐDOC; |
| Б) ∆AOB =∆COD; | Д) ÐBAO =ÐDCO; |
| В) BA = CD; | Е) ÐBAO =ÐCDO. |
1.27°. Знайдіть, користуючись рисунком 1.26, кути трикутника BOC.
| А) 48º, 48º, 84º; | В) 24º, 132º, 24º; | |
| Б) 132º, 48º, 48º; | Г) 42º, 90º, 48º; | Д) 48º, 132º, 20º. |
1.28°. Ідентифікуйте кожному шестикутнику периметра Р, коло, радіуса R, описаного навколо нього.
А)  см; см;
| 1)  см; см;
|
Б) 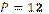 см; см;
| 2)  см; см;
|
В)  см; см;
| 3)  см; см;
|
Г) 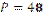 см; см;
| 4)  см; см;
|
Д)  см. см.
| 5)  см. см.
|
| А | |
Б 
| |
| В | |
| Г | |
| Д |

1.29°. Обчисліть периметр трикутника з вершинами у центрах трьох кіл з радіусами 6 см, 7 см і 8 см, що попарно дотикаються зовні (рис.1.27).
| А) 28 см; | В) 27 см; | |
| Б) 29 см; | Г) 42 см; | Д) 21 см. |
1.30°.Виберіть вирази, якими визначаються радіус вписаного кола у правильний трикутник зі стороною а та радіус описаного навколо нього кола:
1)  ; ;
| 2) 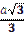 ; ;
| 3)  ; ;
| 4)  ; ;
| 5)  . .
|
| А) 1 і 2; | Б) 2 і 3; | В) 3 і 4; | Г) 4 і 5; | Д) 1 і 5. |

1.31°. Знайдіть діаметр кола, якщо пряма a є дотичною до нього,
A – точка дотику, OB = 12 см та утворює з дотичною кут 30º (рис.1.28).
| А) 24 см; | Б)12 см; | В) 6 см; | Г) 18 см; | Д) 4 см. |
1.32°. Сторона квадрата  см. Укажіть довжину радіуса кола,
см. Укажіть довжину радіуса кола,
вписаного у цей квадрат.
| А) 20 см | Б) 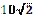 см см
| В) 10 см | Г)  см см
| Д) 5 см. |
 1.33°. Одна з основ трапеції на 8 см більша за іншу, а середня лінія трапеції дорівнює 10 см. Знайдіть меншу основу трапеції.
1.33°. Одна з основ трапеції на 8 см більша за іншу, а середня лінія трапеції дорівнює 10 см. Знайдіть меншу основу трапеції.
| А) 2 см; | Б) 4 см; | В) 6 см; | Г) 8 см; | Д) 10 см. |
 1.34°. Обчисліть площу ромба, діагоналі якого дорівнюють 10 см і 36 см.
1.34°. Обчисліть площу ромба, діагоналі якого дорівнюють 10 см і 36 см.
| А) 90 см2; | Б) 92 см2; | В) 180 см2; | Г) 184 см2; | Д) 360 см2. |
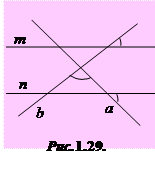
1.35°°. Знайдіть, користуючись даними рисунка 1.29, кут між прямими a і b,
якщо прямі m і n паралельні.
| А) 50º; | Б) 80º; | В) 100º; | Г) 65º; | Д) 115º. |
1.36°°. Визначте довжини радіусів двох кіл, що дотикаються зовні, якщо відстань між їх центрами 18 см, а довжина одного з них становить 50 % довжини іншого.
| А) 9 см і 6 см; | В) 12 см і 6 см; | |
| Б)10 см і 8 см; | Г) 14 см і 4 см; | Д) 24 см і 12 см. |
1.37°°. Укажіть вираз, що визначає довжину кола, яке обмежує круг площею см2.
| А) см; | Б) см; | В)  см; см;
| Г) 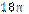 см; см;
| Д) см. |
1.38°°. Знайдіть площу круга, вписаного в квадрат зі стороною 6 см.
| А) см2; | Б) 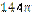 см2; см2;
| В)  см2; см2;
| Г) 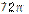 см2; см2;
| Д) 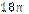 см2. см2.
|

1.39°°. Знайдіть площу трикутника, користуючись даними рисунка 1.30, де довжини відрізків наведені в см.
| А) 6 см2; | Б) 9 см2; | В)12 см2; | Г) 24 см2; | Д) 30 см2. |
1.40°°. Визначте периметр рівнобедреного трикутника, якщо точка дотику, вписаного у нього кола, ділить його бічну сторону на відрізки 6 см і 5 см. Виберіть правильну комбінацію можливих відповідей.
| 1) 21 см; | 2)32 см; | 3) 23 см; | 4) 34 см; | 5) 33 см. |
| А) 1 або 2; | Б) 2 або 4; | В) 2 або 3; | Г) 3 або 5; |  Д) 4 або 5. Д) 4 або 5.
|
1.41°°. Знайдіть сторону ВС трикутника ABC, який вписано в коло
радіуса R
(рис.1.31).
| А) R; | Б) 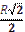 ; ;
| В)  ; ;
| Г)  ; ;
| Д)  . .
|
1.42°°. Ідентифікуйте парами сторону правильного трикутника а та відповідний
радіус r вписано в нього кола.
А) 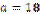 см; см;
| 1)  см; см;
| А | |
Б)  см; см;
| 2) 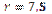 см; см;
| Б 
| |
В) 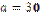 см; см;
| 3)  см; см;
| В | |
Г) 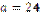 см; см;
| 4) 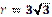 см; см;
| Г | |
Д) 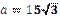 см. см.
| 5)  см. см.
| Д |
1.43°°. Радіус кола, вписаного в квадрат, дорівнює 5 см. Знайдіть діагональ квадрата.
| А) см; | Б)  см; см;
| В)  см; см;
| Г)  см; см;
| Д)  см. см.
|
 1.44°°. На рисунку 1.32 зображено два трикутники АВС і СDМ, сторони яких АВ і MD – паралельні. Знайдіть довжину відрізка AD, якщо
1.44°°. На рисунку 1.32 зображено два трикутники АВС і СDМ, сторони яких АВ і MD – паралельні. Знайдіть довжину відрізка AD, якщо  ,
,  см.
см.
| А) 3 см; | Б) 4,5 см; | В) 6 см; | Г) 7,5 см; | Д) 9 см. |
1.45°°. Укажіть кількість сторін правильного многокутника, внутрішній кут якого дорівнює  .
.
| А) 12; | Б) 14; | В) 16; | Г) 18; | Д) 20. |
1.46°°. Знайдіть периметр ромба, діагоналі якого дорівнюють 24 см і 18 см.
| А) 120 см; | Б) 60 см; | В) 84 см; | Г) 108 см; | Д) 144 см. |
1.47°°. Відомо, що периметр паралелограма дорівнює 48 см, а одна з його сторін на 8 см довша за іншу. Знайдіть меншу сторону паралелограма.
| А) 8 см; | Б) 16 см; | В) 6 см; | Г) 12 см; | Д) 10 см. |
1.48°°. Зовні рівнобедреного трикутника ABC побудували два рівні кути ABM і CBK, сторони яких перетнули продовження основи AC відповідно у точках M і K. Доведіть рівність трикутників MBC і KBA (рис. 1.33а).
1.49°°. З точки кола проведено дві взаємно перпендикулярні хорди довжиною 5 см і 12 см. Знайдіть відстань між кінцями хорд.
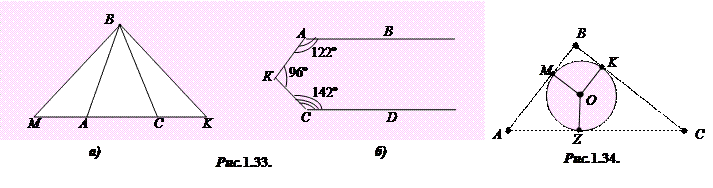
1.50·. Визначте взаємне розміщення двох прямих AB і CD за даними рисунка 1,33б. Відповідь обґрунтуйте.
1.51·. У трикутник ABC вписано коло (рис. 1.34), точки дотику якого M, Z поділяють дві його сторони AB i AC на відрізки, різниця яких відповідно дорівнює 3 см і 4 см (AM>MB, AZ>ZC). Знайдіть сторони трикутника ABC, якщо його периметр дорівнює 28 см.
1.52·. Навколо рівностороннього трикутника описане коло, радіус якого дорівнює  см. Обчисліть радіус вписаного кола.
см. Обчисліть радіус вписаного кола.
1.53·. Навколо кола описана рівнобічна трапеція, кут при основі якої дорівнює  Висота трапеції – 7 см. Знайдіть довжину середньої лінії трапеції.
Висота трапеції – 7 см. Знайдіть довжину середньої лінії трапеції.
1.54·. Навколо кола описана рівнобічна трапеція, кут при основі якої дорівнює  Середня лінія трапеції дорівнює
Середня лінія трапеції дорівнює  см. Знайдіть довжину висоти трапеції.
см. Знайдіть довжину висоти трапеції.
1.55·. Знайдіть бічну сторону рівнобедреного трикутника, основа якого дорівнює 16 см, а висота проведена до неї, – 15 см.
1.56·. Висота АМ трикутника АВС ділить його сторону ВС на відрізки ВМ і МС. Знайдіть довжину відрізка МС, якщо  см,
см, 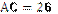 см,
см, 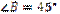 .
.
1.57·. Сторона ромба дорівнює 10 см, а одна з діагоналей – 12 см. Знайдіть радіус вписаного в ромб кола.
1.58·. У колі, радіусом 15 см, на відстані 12 см від його центра проведено хорду. Знайдіть довжину цієї хорди.
1.59·. Бісектриса тупого кута паралелограма ділить його сторону на відрізки 6 см і 10 см, рахуючи від вершини гострого кута. Обчисліть площу паралелограма, якщо його гострий кут дорівнює  .
.
1.60··. У колі проведено дві хорди, що перетинаються. Одна із них точкою перетину поділилася навпіл, а друга – на частини довжиною 5 см і 20 см. Знайдіть довжину кожної хорди.
1.61··. З точки поза колом проведено січну і дотичну. Знайдіть довжину дотичної, якщо вона на 5 см більша від зовнішньої частини та на стільки ж менша від внутрішньої частини січної.
1.62··. З точки поза колом проведено січну і дотичну, сума довжин яких дорівнює 15 см, а зовнішня частина січної на 2 см менша від дотичної. Знайдіть довжини січної і дотичної.
1.63··. Знайдіть площу прямокутного трикутника, якщо точка дотику вписаного кола ділить гіпотенузу на відрізки 6 см і 9 см.
1.64··. У прямокутній трапеції менша основа дорівнює 8 см, а менша бічна сторона –  см. Знайдіть площу трапеції, якщо один із її кутів дорівнює
см. Знайдіть площу трапеції, якщо один із її кутів дорівнює  .
.
1.65··. Навколо трапеції, основи якої дорівнюють 40 см і 14 см, а висота – 39 см, описано коло. Знайдіть його радіус.
1.66··. а) Діагоналі трапеції дорівнюють 20 см і 15 см, висота - 12 см. Обчисліть площу трапеції.
б) Діагоналі трапеції дорівнюють 30 см і 26 см, а висота – 24 см. Обчисліть площу трапеції.
1.67··. Більша діагональ ромба дорівнює 24 см, а радіус вписаного кола – 6 см. Обчисліть площу ромба.
1.68··. Сторони трикутника дорівнюють 17 см, 25 см і 28 см. Коло з центром на найбільшій стороні дотикається до двох інших сторін. Обчисліть площу круга.
1.69··. Знайдіть площу паралелограма, якщо його сторони дорівнюють 6 см і 4 см, а кут між діагоналями – 60°.
Переглядів: 5196