• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ЧАСОВИЙ МЕТОД АНАЛIЗУ ПЕРЕХIДНИХ ПРОЦЕСIВ

Порiвняємо рiзнi методи аналiзу перехiдних процесiв.

Класичний метод слушно застосовувати, якщо дiючий сигнал є функцiєю увiмкнення або змiнюється за синусоїдним законом, оскiльки у цьому випадку вимушена складова розраховується за допомогою вiдомих методiв (наприклад, символiчного).

Операторний метод дозволяє аналiзувати процеси у колах при дiї сигналiв довiльної форми. Але, якщо сигнали на входi або виходi кола описуються нестандартними функцiями, для яких не наводяться їх зображення у довiдниках (або цi зображення взагалi не iснують), то розв'язання задачi ускладнюється.

Часовий метод аналiзу перехiдних процесiв рекомендується застосовувати у тих випадках, коли дiя змінюється за складним законом у часі, наприклад, при наявностi стрибкiв напруги або коли дiя задана графiчно.

6.1 Часовi характеристики кола

Згідно з часовим методом аналiзу, аби дослiдити реакцiю ЛЕК при довiльнiй дiї, доцiльно скористатись принципом суперпозицiї:

- у лiнiйному колi вiдгук на суму кiлькох дiй дорiвнює сумi вiдгукiв на кожну дiю, яка дiє окремо.

Припустимо, що функцiю зовнiшньої дiї 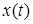можна подати у виглядi сукупностi простих типових функцiй 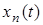, тобто

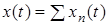. (6.1)

Якщо вiдгук досліджуваного кола на дiю 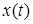дорiвнює 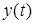, а реакцiя кола на типову дiю 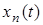дорiвнює 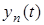, тодi за принципом накладання матимемо

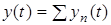. (6.2)

Типовi функцiї (дiї) повиннi мати деякi особливi властивостi:

- як правило, при i при ;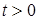

- вони мають бути однотиповими, тодi i реакцiя буде сумою однотипових вiдгукiв;

- пiдсумовування типових дiй має давати можливiсть вiдтворення сигналiв будь-якої форми;

- типова дiя повинна мати реальний (практичний) аналог.

До типових дiй належать: 1) синусоїдний сигнал; 2) одинична функцiя (функцiя увiмкнення) 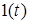; 3) дельта-функцiя 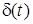. Перша типова дiя застосовується у спектральному (частотному) методi, а двi останнiх - у часовому.

Перед тим, як перейти до часових характеристик, доречно нагадати визначення частотних характеристик кола. Якщо на входi кола дiє гармонiчне коливання 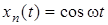, то для визначення вiдгуку 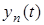у стацiонарному режимi використовується метод комплексних амплiтуд. При змiнюваннi частоти 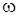вхiдного сигналу змiнюється комплексна амплiтуда вiдгуку 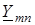. Саме залежнiсть комплексної амплiтуди вiдгуку вiд частоти вхiдного сигналу i зветься частотною характеристикою кола.

Часовими характеристиками кола називатимемо вiдгуки кола на одиничну функцiю 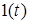i дельта-функцiю 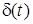. Iнакше кажучи, якщо у формулi (6.1) 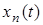дорiвнює 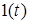або 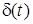, то функцiя 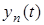є часовою характеристикою. Отже, якщо відомо часовi характеристики, згiдно з (6.2) можна визначити сигнал на виходi .

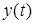6.2 Одинична функцiя. Перехiдна характеристика

Розглянемо першу типову дiю, яка має назву одиничної функцiї, або функцiї увiмкнення (функцiї Хевiсайда). Графiчно ця функцiя показана на рис.6.1а, а аналiтично записується як

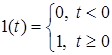. (6.3)

Якщо одинична функцiя має запiзнення , то

.

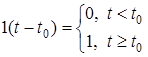За допомогою функцiї можна отримати сигнал (рис.6.1б) 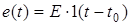, або

.

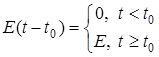
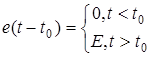а) б)

Рисунок 6.1

П е р е х i д н а характеристика h(t) чисельно дорiвнює реакцiї кола на одиничну функцiю 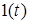1(t) (одиничний стрибок) за нульових початкових умов.

Вимiрнiсть h(t) визначається вiдношенням вимiрностi вiдгуку до вимiрностi одиничного стрибка. Якщо, наприклад, дiю задано у виглядi одиничного стрибка напруги, i вiдгуком є також напруга, то h(t) - безрозмiрна величина. Якщо при такiй самiй дiї як вихiдну величину вибрано струм, то h(t) має вимiрнiсть провiдностi (См).

Розглянемо приклад, коли до послiдовно з’єднаних опору i ємностi пiдключається джерело е.р.с. 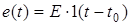EW1(t). Знайдемо перехiднi характеристики, вважаючи вiдгуком спади напруги на опорi та ємностi.

Подiбна задача вже розв'язана вище за класичним методом. За нульових початкових умов (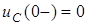u (0-)=0) u = E[1-exp(-t/t)] 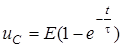; 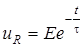u = E[exp(-t/t)]. Щоб знайти h(t), треба прирiвняти Е = 1В. Тодi 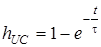h (t) = 1-exp(-t/t); h = exp(-t/t) (рис.6.2а).

а) б)

Рисунок 6.2

6.3 Дельта-функцiя. Iмпульсна характеристика

Розглянемо другу типову дiю, яка має назву дельта-функцiї, або одиничного iмпульсу (функцiї Дiрака). Графiчно ця функцiя показана на рис.6.3а, а аналiтично записується як 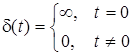d(t) = { .

Якщо дельта-функцiя має запiзнення t , то

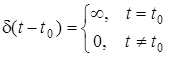d(t-t ) = { .

а) б)

Рисунок 6.3

Отже, дельта-функцiя має нескiнченно велике значення на нескiнченно малому iнтервалi часу, поза цим iнтервалом функцiя дорiвнює нулю, причому площа 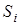S , яка обмежена цiє'ю функцiєю, дорiвнює одиницi, тобто

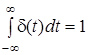d(t)dt = 1 ; d(t-t )dt = 1 .

Поняття дельта-функцiї зручно розглянути, скориставшись iмпульсом прямокутної форми (рис.6.3б; 6.4а, б). Для цього подамо прямокутний iмпульс за допомогою двох одиничних функцiй.

а) б)

Рисунок 6.4

Якщ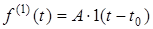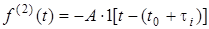о , , то

.

Якщо f (t) = AW1(t-t ) , f (t) = - AW1[t-(t +t )] ,

то f (t) = f (t) + f (t) = AW[1(t-t )-1(t-t -t )] .

Згiдно з визначенням, одиничний iмпульс має одиничну площу. (тТому вiн i має таку назву). Тодi амплiтуда A може бути знайдена, виходячи з рiвняння S = 1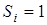; AWt = 1; A = 1/t.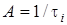

Вираз Ддельта-функцiїю отримаємо, скориставшись граничним переходом

lim f (t)= lim ДДДДДДДДДДДДДДДДДДДД = ДДДДДДДДД = d(t-t ). (6.4)

Для пiдтвердження зв'язку 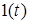1(t) i 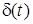d(t) продиференціюємо за часом допомiжну функцiю f (t) (рис.6.5). Легко побачити, що

f' (t) = { i i .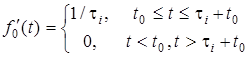

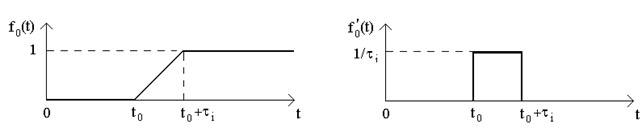
Рисунок 6.5

При t L 0 функцiя f (t) переходить в одиничний стрибок

1(t-t ), а її похiдна перетворюється на дельта-функцiю.

Доречно зазначити, що дельта-функцiя є математичною абстракцiєю, але її можна вважати iдеалiзованим випадком реальної дiї у виглядi однополярного короткочасового iмпульсу. Малу тривалiсть цього iмпульсу треба розумiти так, що вона значно менша часу практичної тривалостi перехiдного процесу ( t = 4,6t , t , t ).

Дельта-функцiя має фiльтрувальну властивiсть, яка широко використовується у теорії кілв ТЕК: f(t)d(t)dt=f(0); f(t)d(t-t )dt= f(t ).

Наприклад, якщо функцiю f(t) задано, як показано на (рис.6.6), то

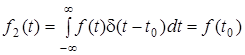f (t) = f(t)d(t-t )dt = f(t ) .

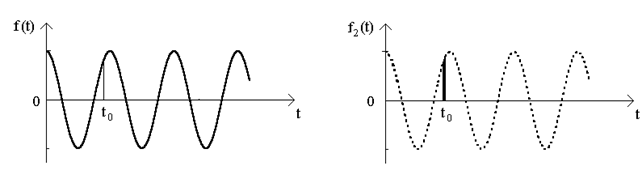
Рисунок 6.6

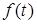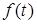Доведення. Оскiльки за визначенням d(t-t ) вiдрiзняється вiд нуля лише у точцi t = t , то в силу неперервностi функцiї f(t) можна припустити, що в момент часу t = t функцiя f(t) прийме постiйне значення i може бути винесена з-пiд знака iнтеграла:.

f (t) = f(t ) d(t-t )dt = f(t ) ,.

причому за визначенням дельта-функції значення iнтеграла дорiвнює одиницi.

Отже, пiсля докладного розгляду властивостей дельта-функцiї, дамо визначення iмпульсної характеристики.

I м п у л ь с н а характеристика g(t)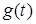чисельно дорiвнює реакцiї кола на одиничний iмпульс (дельта-функцiю) за нульових початкових умов. Вимiрнiсть 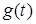визначається вiдношенням вимiрностi вiдгуку до вимiрностi одиничного iмпульсу, помноженої на секунду. Якщо, наприклад, дiю задано у виглядi напруги, а вiдгуком є струм, то iмпульсна характеристика має вимiрнiсть А/(В×с).

6.4 Зв'язок мiж h(t) i g(t)

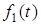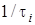Нехай до кола, для якого вiдома перехiдна характеристика h(t), пiдведена дiя у виглядi вiдеоiмпульсу прямокутної` форми f (t), тривалiстю t i амплiтудою 1/t , площа якого дорiвнює одиницi. Подамо цей iмпульс у виглядi суми ступінчастих дiй (рис.6.7): 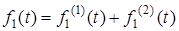f (t) = f + f .

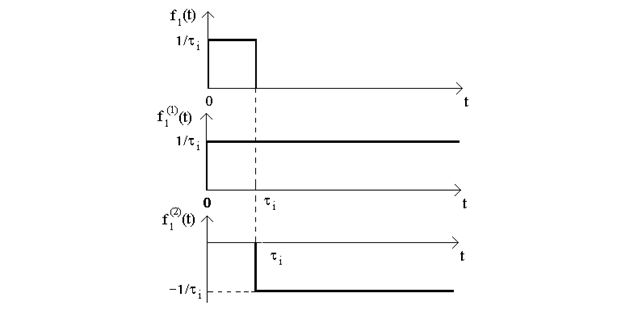
Рисунок 6.7

Користуючись визначенням перехiдної характеристики, можна записати реакцiю кола на кожну з цих дiй:

а) 0 < t < t 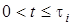, f (t) = f = (1/t )h(t);

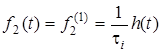б) 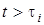t > t , 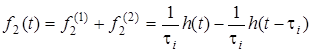f (t) = f + f = (1/t )h(t)-(1/t )h(t-t ).

Знак "-" пояснюється тим, що "стрибок" 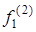f є вiд''ємним. Тодi реакцiя кола на iмпульс 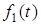f (t) вiдповiдно до теореми накладання становитиме

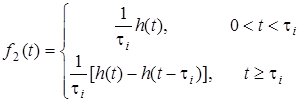f (t) = { .

Нехай тривалiсть iмпульсу прямує до нуля, але площа iмпульсу зберiгається незмiнною. При цьому дiя 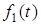f (t) переходить у дельта-функцiю (див. формулу (6.4)), тодi f (t) за визначенням переходить в iмпульсну характеристику 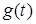g(t). Тобто lim f (t)=g(t). Граничний перехiд у тому випадку, коли 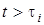t >t , дає

дає

g(t) = lim ДДДДДДДДДДДДДД або 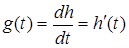g(t) = ДД = h'(t).

У разi, коли 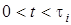0 < t < t , iмпульсну дiю при t L 0 можна розглядати, як ступінчасту дiю з амплiтудою 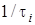1/t . Тодi, згiдно з визначенням, реакцiя на iмпульсну дiю дорiвнює 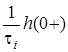(1/t )h(0+):

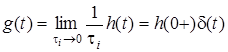g(t) = lim (1/t )h(t) = h(0+)d(t) .

Отже, 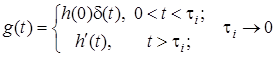g(t) = { t L 0 ,

або

g(t) = h(0)d(t) + h'(t) . (6.6)

Отриманi спiввiдношення дозволяють розв’язати i обернену задачу: за вiдомою 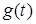g(t) знайти h(t): h(t) = g(t)dt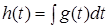. Оскiльки 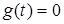g(t) = 0 при , то пiсля переходу вiд невизначеного iнтегралу до iнтегралу зi змiнною верхньою границею, матимеємо

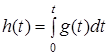h(t) = g(t)dt . (6.7)

Остання формула виконується як при 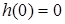h(0)=0, так i при h(0)$0.

Знайдемо iмпульсну характеристику для кола, яке розглянуто у попередньому прикладi. Як правило, за класичним методом 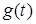g(t) не визначають безпосередньо, а використовують її зв'язок з перехiдною характеристикою h(t), тобто вираз (6.6). У даному випадку при 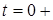t=0+ 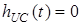h (t)=0; h = 1. Тодi для напруги на ємностi 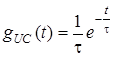g(t)=(1/t)exp(-t/t), а для напруги на опорi 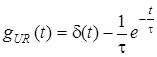g(t) = d(t) - (1/t)exp(-t/t), де t - стала часу. Вiдповiднi графiки зображено на рис.6.2б.

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. Метод рiвних вiдрiзкiв.
5. VII. Нахождение общего решения методом характеристик
6. А. науковий факт, b. гіпотеза, с. метод
7. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
8. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
9. АгротехнІЧНИЙ метод
10. Адаптовані й специфічні методи дослідження у журналістикознавстві
11. Адміністративні (прямі) методи регулювання.
12. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.

Переглядів: 1889