
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теорема Чебишева
Інтеграл від диференціального бінома 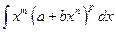 виражається через інтеграл від раціональної функції відносно нової змінної, якщо:
виражається через інтеграл від раціональної функції відносно нової змінної, якщо:
1)  - ціле число (додатне, від’ємне чи 0) і виконано підстановку
- ціле число (додатне, від’ємне чи 0) і виконано підстановку 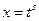 , де
, де 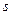 - найменший спільний знаменник дробів
- найменший спільний знаменник дробів  і
і  ;
;
2) 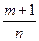 - ціле число (додатне, від’ємне чи 0) і виконано підстановку
- ціле число (додатне, від’ємне чи 0) і виконано підстановку  , де
, де 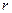 - знаменник дробу
- знаменник дробу  ;
;
3) 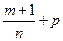 - ціле число (додатне, від’ємне чи 0) і виконано підстановку
- ціле число (додатне, від’ємне чи 0) і виконано підстановку  , де
, де 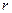 - знаменник дробу
- знаменник дробу  .
.
В інших випадках інтеграл від диференціального біному через елементарні функції не виражається.
- Інтеграл виду
 раціоналізується підстановкою
раціоналізується підстановкою  , яка називається універсальною.
, яка називається універсальною.
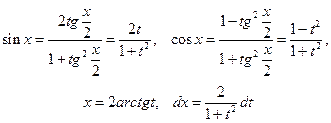
a)  , підстановка
, підстановка 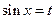 ;
;
b) 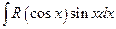 , підстановка
, підстановка  ;
;
c)  , підстановка
, підстановка 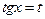 ;
;
d)  , підстановка:
, підстановка:
1)  , якщо функція
, якщо функція  непарна відносно
непарна відносно 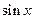 ,
,  ,
,
2) 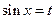 , якщо функція
, якщо функція  непарна відносно
непарна відносно  ,
,  ,
,
3) 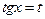 , якщо функція
, якщо функція  парна відносно
парна відносно 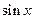 і
і  одночасно,
одночасно,  ;
;
e)  , підстановка:
, підстановка:
1) 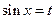 , якщо
, якщо  - ціле додатне непарне число;
- ціле додатне непарне число;
2)  , якщо
, якщо  - ціле додатне непарне число;
- ціле додатне непарне число;
3) за допомогою формули пониження степеня  , якщо
, якщо  і
і  - цілі додатні парні числа;
- цілі додатні парні числа;
4) 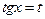 , якщо
, якщо  і
і  - цілі парні числа, але одне з них від’ємне або цілі парні і від’ємні.
- цілі парні числа, але одне з них від’ємне або цілі парні і від’ємні.
f)  обчислюються за допомогою формул
обчислюються за допомогою формул
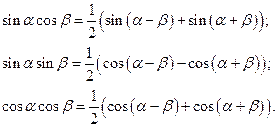
- Інтеграл виду
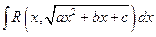 обчислюється за допомогою підстановки
обчислюється за допомогою підстановки 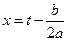 або підстановки Ейлера:
або підстановки Ейлера:
1) якщо 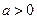 , то
, то 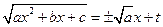 ;
;
2) якщо 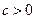 , то
, то  ;
;
3) якщо 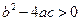 , то
, то 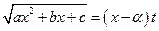 , де
, де 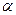 - корінь тричлена
- корінь тричлена 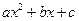 .
.
- Інтеграл
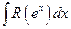 раціоналізується підстановкою
раціоналізується підстановкою  .
.
6. Інтеграли, що „не беруться”
1) 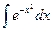 - інтеграл Пуассона;
- інтеграл Пуассона;
2) 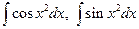 - інтеграли Френеля;
- інтеграли Френеля;
3) 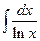 - інтегральний логарифм;
- інтегральний логарифм;
4) 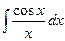 - інтегральний косинус;
- інтегральний косинус;
5) 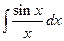 - інтегральний синус;
- інтегральний синус;
6) 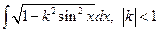 - еліптичний інтеграл;
- еліптичний інтеграл;
7) 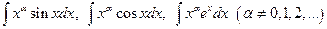 та ряд інших інтегралів.
та ряд інших інтегралів.
Читайте також:
- В. Друга теорема про розклад.
- Друга теорема Вейєрштрасса
- Інтегральна теорема Лапласа
- Локальна теорема Лапласа
- Магнітний потік. Теорема Гауса для магнітного поля
- Момент інерції. Теорема Гюйгенса-Штейнера
- Напряженность поля. Теорема Гаусса
- Незалежні події. Теорема множення для незалежних подій
- Опукле програмування. Необхідні та достатні умови існування сідлової точки. Теорема Куна-Такера.
- Основна теорема арифметики цілих невід’ємних чисел.
- Потік вектора напруженості та індукції електричного поля. Теорема Остроградського-Гауса
- Приведення сили до точки (теорема Пуансо)
| <== попередня сторінка | | | наступна сторінка ==> |
| Метод інтегрування частинами | | | ЛЕКЦІЯ 15. Гегельянство та неогегельянство |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |