• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Арифметичні операції в різних системах числення

Зв'язок двійкової та шістнадцяткової систем

Розглянемо простий спосіб переведення шістнадцяткового числа у двійкове та навпаки. Оскільки 16 = 2⁴ = 10000₂, то одна шістнадцяткова цифра використовується для зображення чотирьох бітів:

0 - 0000, 1 - 0001, 2 - 0010, 3 - 0011, 4 - 0100, 5 - 0101, 6 - 0110, 7 - 0111, 8 - 1000, 9- 1001, А- 1010, В- 1011, С- 1100, D- 1101, Е- 1110, F - 1111.

Отже, для переведення двійкового числа у шістнадцяткове достатньо у двійковому записі, починаючи з наймолодшої цифри, замінити кожні чотири біти відповідними шістнадцятковими цифрами (якщо найстарша четвірка розрядів неповна, до неї дописуються незначущі нулі). Навпаки, шістнадцятковий запис переводиться в двійковий заміною цифр відповідними четвірками бітів. Четвірка бітів, що відповідає найстаршій шістнадцятковій цифрі, може мати незначущі нулі у старших розрядах.

При переведенні дробових чисел четвірки розрядів слід виділяти, починаючи від найближчого до коми розряду як у цілій, так і у дробовій частині числа. При цьому до неповних четвірок дописуються нулі (йдеться про наймолодшу четвірку розрядів у дробовій частині та найстаршу четвірку у цілій частині числа).

Приклад1.5________________________________________________________

Перевести в шістнадцяткову систему числення двійкове число 1111010. Спочатку число, починаючи від молодшої цифри, розбивають на групи: 1010 та 111. Старша група доповнюється до тетради 0111. Цій тетраді відповідає шістнадцяткова цифра 7, а тетраді 1010 — цифра А. Отже, результатом переведення є 7А. Тепер зобразимо у двійковому вигляді шістнадцяткове число А7. Шістнадцяткова цифра А зображує двійкове число 1010, а шістнадцяткова цифра 7 — двійкове число 111. Доповнивши двійковий запис числа 7 нулем у старшому розряді, отримаємо А7₁₆= 10100111₂.

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

Основними арифметичними операціями у системі команд будь-якого комп'ютера є додавання, віднімання, множення та ділення. Правила виконання цих операцій У десятковій системі числення загальновідомі. Вони застосовуються і при виконанні аналогічних дій в інших позиційних системах числення.

Розглянемо операцію додавання двійкових чисел. У десятковій системі 9+1=10, a y двійковій 1+1 = 10. Таким чином, при додаванні у стовпчик двох одиничних розрядів отримаємо нульовий розряд суми і одиницю перенесення у наступний, старший розряд. Додамо у стовпчик числа 11₂ і 110₂, вказуючи розряди перенесень у дужках.

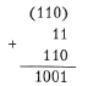
Додавання у системі числення з довільною основою Р виконується аналогічно тому, як це робиться у десятковій та двійковій системах. При додаванні двох однорозрядних Р-кових чисел а₁ і а₂ обчислюється сума S=а₁+а₂, і результатом є (S div P)S mod Р, де в дужках вказано одиницю перенесення у наступний розряд, S div Р - ціла частина, a S mod P - остача від ділення S на Р. При додаванні багаторозрядних Р-кових чисел, починаючи від молодших розрядів, обчислюються суми розрядів і одиниць перенесення від попереднього розряду. Остача від ділення на Р залишається у відповідному розряді результату, а частка переноситься в наступний розряд.

Приклад 1.6________________________________________________________

У цьому прикладі обчислимо суму двох десяткових чисел 548₁₀ і 54₁₀, а також їх вісімкових та шістнадцяткових еквівалентів - 1044₈ і 66₈, 224₁₆ і 36₁₆ (y дужках зверху над значеннями доданків вказуються одиниці перенесення у відповідні розряди).

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

Віднімання в будь-якій системі числення виконується за тими самими правилами, що й у десятковій.

Приклад 1.7______________________________________________________

Віднімемо одиницю від чисел 100₂, 100₈ і 100₁₆:

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

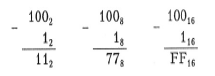
Операцію множення у довільній системі числення можна виконати за допомогою методу, який подібний до методу множення у стовпчик. Обчислення добутку двох n-розрядних чисел без знака зводиться до формування часткових добутків для кожної цифри множника і їх подальшого додавання. Коли обидва операнди є двійковими числами, процедура обчислення часткових добутків значно спрощується: якщо цифра множника дорівнює нулю, то і частковий добуток теж становить нуль, якщо одиниці, частковий добуток дорівнює значенню множеного. Перед додаванням кожний частковий добуток необхідно зсунути на один розряд вліво відносно попереднього добутку. Таким чином, результатом множення двох n-розрядних двійкових чисел може бути число, яке має 2n розрядів.

Приклад 1.8_______________________________________________________

Обчислимо добуток двох чисел у десятковій, вісімковій і шістнадцятковій системах числення. Співмиожниками будуть числа 29₁₀=35₈=1D₁₆, 19₁₀ = 23₈=

Читайте також:

1. Автододавання та автообчислення.
2. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
3. Активні операції банків
4. Активні операції комерційних банків
5. Алг W2 (ОБЧИСЛЕННЯ Y)
6. Алгебраїчні операції
7. Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
8. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
9. Аналітичні показники динаміки та прийоми їх обчислення
10. Арифметичні оператори
11. Арифметичні операції

Переглядів: 9870