• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Швидкість і прискорення

Скалярну величину, яка рівна довжині траєкторії 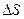називають шляхом. Вектор, що з’єднує початкове положення матеріальної точки з її положенням в даний момент часу називають вектором переміщення .

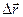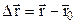. (1.3)

При прямолінійному русі вектор переміщення співпадає з відповідною ділянкою траєкторії, тобто його модуль рівний пройденому шляху. У випадку криволінійного руху вектор переміщення є січною, що проходить через дві точки траєкторії, які відповідають двом різним моментам часу.

Швидкість – це векторна величина, яка характеризує зміну радіуса-вектора рухомої точки з часом. Вектор середньої швидкості рівний відношенню приросту радіуса-вектора 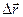рухомої точки до часу , за який він відбувся

. (1.4)

Якщо перейти до границі при , то отримаємо вираз для миттєвої швидкості

. (1.5)

Таким чином,миттєва швидкість – це швидкість в даний момент часу або в даній точці траєкторії. Вектор миттєвої швидкості дорівнює першій похідній радіуса-вектора рухомої точки по часу і напрямлений вздовж дотичної до траєкторії в будь-якій її точці. Врахувавши, що при 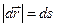, отримаємо:

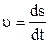. (1.6)

В загальному випадку з (1.6) випливає, що шлях може бути обчислений за формулою

. (1.7)

Швидкість можна представити через її проекції на координатні вісі

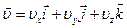, (1.8)

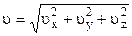, (1.9)

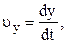
де , 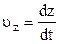. (1.10)

Швидкість може змінюватись як за модулем так і за напрямком. Для характеристики зміни швидкості вводять вектор прискорення, який описує зміну швидкості з часом. Середнє прискорення рівне відношенню зміни швидкості до проміжку часу, за який вона відбулася

. (1.11)

Миттєве прискорення – це прискорення в даний момент часу і воно визначається як границя до якої прямує середнє значення прискорення, якщо проміжок часу прямує до нуля

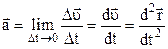. (1.12)

Таким чином, миттєве прискорення дорівнює першій похідній швидкості по часу або другій похідній радіуса-вектора по часу.

В проекціях на координатні вісі

, (1.13)

, (1.14)

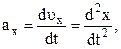
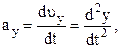
де 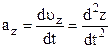. (1.15)

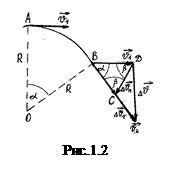
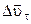Коли матеріальна точка рухається по криволінійній траєкторії (рис.1.2), і вектор її швидкості змінюється як за напрямком так і за модулем , то

. (1.16)

Знайдемо миттєве прискорення матеріальної точки, скориставшись формулами (1.12) та (1.16)

. (1.17)

Отже, повне прискорення рівне сумі нормального 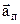і тангенціального прискорень. Нормальне прискорення характеризує зміну швидкості за напрямком і напрямлене вздовж радіуса до центра кривизни траєкторії. Тангенціальне прискорення характеризує зміну швидкості за модулем і напрямлене вздовж дотичної до траєкторії. Числові значення цих прискорень рівні

(1.18)

та 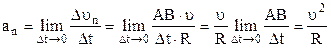. (1.19)

З рис.1.3 маємо

(1.20)

та 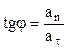. (1.21)

Читайте також:

1. Vу -швидкість ударника
2. Вектори кутової швидкості і кутового прискорення.
3. Векторні характеристикимеханічного руху– переміщення, шлях, швидкіст та прискорення
4. Видаток і середня швидкість ламінарного потоку.
5. Вимірювання інформації та швидкість її передачі
6. Вільне падіння тіл. Прискорення вільного падіння.
7. Вплив параметрів режиму буріння на механічну швидкість проходки
8. Групова швидкість і дисперсія хвиль
9. Етапи, швидкість і показники адаптації
10. Закон грошового обігу та швидкість обігу грошей.
11. На скільки збільшиться маса - частинки (в а.о.м.), якщо її швидкість збільшиться від 0 до 0,9с? Вважати,що маса спокою - частинки 4 а.о.м.
12. Напрямки прискорення оборотності оборотних коштів

Переглядів: 7353