
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Генератори псевдовипадкових бітів
2.1. Означення генератора псевдовипадкових послідовностей.Упродовж попередніх розділів ми використовували випадкові послідовності бітів із двоякою метою: по-перше, у ймовірнісних алгоритмах, і по-друге, у криптосистемах. Звернемо увагу, що випадкові послідовності застосовувалися не лише у ймовірнісних криптосистемах, де це робилося цілком явно, але й у класичних криптосистемах, де таємний ключ слід було вибирати випадковим чином. Типовим прикладом є шифр одноразового блокноту.
Нагадаємо, що випадковою послідовністю бітів довжини п називається випадкова величина, яка набуває кожне значення із {0,1}n з однаковою ймовірністю 2-n. Для невеликого п випадкову послідовність, отримати нескладно, наприклад, підкиданням монетки. Однак породження довгої випадкової послідовності бітів є вельми нетривіальним завданням для обчислювальної машини.
Цей розділ нашого курсу присвячений такому питанню. Припустимо, що ми вміємо генерувати випадкову двійкову послідовність довжини п. Яким чином її можна розширити до випадкової у певному сенсі двійкової послідовності довжини nd, де d є деякою константою? Під словом "розширити" маємо на увазі "перетворити за допомогою детермінованого алгоритму". Зрозуміло, що внаслідок такого розширення ми не зможемо отримати справжню випадкову послідовність довжини nd хоча б тому, що серед всіх 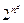 таких послідовностей з ненульовою ймовірністю з'являтимуться щонайбільше 2". Однак хотілося б отримати принаймні псевдовипадкову послідовність довжини nd, тобто послідовність, яка виглядала б як випадкова. Метою серії означень нижче є уточнити і формалізувати останню фразу.
таких послідовностей з ненульовою ймовірністю з'являтимуться щонайбільше 2". Однак хотілося б отримати принаймні псевдовипадкову послідовність довжини nd, тобто послідовність, яка виглядала б як випадкова. Метою серії означень нижче є уточнити і формалізувати останню фразу.
Означення 2.1. Ансамблем будемо називати послідовність випадкових величин Zn, де п  N, які набувають значення у множині війкових слів.
N, які набувають значення у множині війкових слів.
Означення 2.2. Ансамблі {Хn}n N і {Уп}n
N і {Уп}n N називаються нерозрізнюваними за поліноміальний час, якщо для будь-якого поліноміального ймовірнісного алгоритму А
N називаються нерозрізнюваними за поліноміальний час, якщо для будь-якого поліноміального ймовірнісного алгоритму А

для довільної константи с при досить великих п. Тут Р [A(Zn) = 1] позначає ймовірність того, що алгоритм А, отримавши на вхід випадкову величину Zn, подасть на вихід 1. Ймовірність береться як за розподілом Zn, так і за розподілом випадкової послідовності ймовірнісного алгоритму А.
Означення 2.3. Нехай l: N —> N — функція така, що l(п) > п. Генератором із розширенням l називається поліноміальний детермінований алгоритм G, який двійкову послідовність х  {0,1}n перетворює у послідовність G(x)
{0,1}n перетворює у послідовність G(x)  {0,1}l(n) .
{0,1}l(n) .
Випадкову послідовність х, що подається на вхід генератора, називатимемо паростком. Задля технічної зручності домовимось, що для деяких паростків х генератор G може видавати відмову, і тоді G(x) буде невизначеним.
Тепер домовимось, які генератори заслуговують бути названими генераторами псевдовипадкових послідовностей або, коротше, псевдовипадковими генераторами. Визначальною рисою такого генератора G: {0,1}n —> {0, 1}l(n) має бути те, що випадкову величину G(x), де х — випадковий паросток із {0,1}n, ніяким поліноміальним ймовірнісним алгоритмом не можна відрізнити від випадкової величини, рівномірно розподіленої на {0, 1}l(n).
Означення 2.4. Нехай G — генератор із розширенням l. Позначимо через Zl(n) випадкову величину G(x) зі значеннями в {0,1}l(n), для х рівномірно розподіленого на {0,1}n. Через Un позначимо випадкову величину з рівномірним розподілом на {0,1}n. Генератор G називається псевдовипадковим, якщо ансамблі {Zl(n)}n N i {Ul(n)}n
N i {Ul(n)}n N нерозрізнювані за поліноміальний час.
N нерозрізнювані за поліноміальний час.
Двійкову послідовність G(x), отриману за допомогою псевдовипадкового генератора G із випадкового паростка х, будемо називати псeвдовипадковою.
Здавалося б, що розширення l є важливою кількісною характеристикою генератора псевдовипадкових послідовностей. Однак, наступне твердження дещо несподівано виявляє, що величина l не відіграє надто принципової ролі — генератор з мінімальним розширенням можна перетворити в генератор з довільним поліноміальним розширенням.
Твердження 2.5. [О.Гольдрайх, С.Mікелі] 3 довільного псевдовипадкового генератора G з розширенням 1(п) = п + 1 можна отримати псевдовипадковий генератор G' із розширенням l'(n) = nd для довільної цілої константи d > 1.
Доведення. Винесене у вправу 2.1.
Псевдовипадкові генератори цілком придатні для використання у ймовірнісних алгоритмах. Якщо алгоритм потребує випадкової послідовності довжини nd, то замість неї можна використовувати псевдови-падкову послідовність такої ж довжини, отриману із справді випадкового паростка довжини п (див. вправу 2.3).
2.2. Непередбачуваність псевдовипадкових генераторів. У криптографічних застосуваннях від псевдовипадкового генератора G вимагається виконання такої умови. Нехай суперник спостерігає випадкову величину G(x), розподілену на {0, 1}l(n) і породжену рівномірним розподілом паростка х на {0, 1}n. Припустимо, що спочатку йому відкриваються лише перші і бітів величини G(x) . Тоді бажано, щоб суперник не міг передбачити (i + 1)-ий біт з імовірністю, суттєво кращою за 1/2. Іншими словами, ми зацікавлені, щоб не було кращого шляху отримати (і + 1)-ий біт на основі знання всіх попередніх бітів, аніж простим підкиданням монетки.
Зв'язок цієї вимоги із криптографічною надійністю можна пояснити таким прикладом. Припустимо, що суперник перехопив криптотекст у двійковому алфавіті, і йому відомі такі факти:
1) вжито шифр одноразового блокноту;
2) ключ є псевдовипадковою послідовністю;
3) відкритий текст починається зверненням „Вельмишановний Іване Івановичу”.
Тоді додавши відомий йому префікс відкритого тексту до відповідного префіксу криптотексту, суперник отримає перші і бітів псевдовипадкового ключа. Якщо генератор, який було використано для вибору ключа, не володіє описаною вище властивістю, то суперник зможе екстраполювати наступні біти ключа і добути із криптотексту ще більше інформації.
Означення 2.6. Нехай для кожного натурального п випадкова величина Zn набуває значення в {0,1}n. Ансамбль {Zn}n N називається непередбачуваним або, як ще кажуть, витримує тестування наступного біту, якщо виконується така умова. Припустимо, що sσ — префікс випадкового слова Zn, де σ
N називається непередбачуваним або, як ще кажуть, витримує тестування наступного біту, якщо виконується така умова. Припустимо, що sσ — префікс випадкового слова Zn, де σ  {0,1} і s
{0,1} і s  {0, 1}k-1, причому довжина k цього префіксу є випадковим числом від 1 до п. Нехай А — довільний поліноміальний ймовірнісний алгоритм, який отримує на вхід s. Тоді
{0, 1}k-1, причому довжина k цього префіксу є випадковим числом від 1 до п. Нехай А — довільний поліноміальний ймовірнісний алгоритм, який отримує на вхід s. Тоді
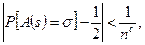
для довільної константи с при досить великих п.
Виявляється, що псевдовипадкові генератори і лише вони володіють властивістю непередбачуваності.
Теорема 2.7. Нехай G: {0,1)n—> {0,!}l(n) — генератор із розширенням l. Позначимо через Zl(n) випадкову величину G(x) зі значеннями в {0,1}l(n), для х рівномірно розподіленого на {0,1}n. Генератор G є псевдовипадковим тоді і лише тоді, коли ансамбль {Zn}п N непе-
N непе-
редбачуваний.
На підставі цієї теореми і в світлі попереднього обговорення псевдовипадкові генератори часом називають криптографічна надійними.
2.3. Псевдовипадкові генератори із важкооборотних перестановок. Нехай f — важкооборотна функція, яка після фіксації відповідних параметрів є перестановкою деякої множини Dn, причому [log||Dn||] = п. Прикладами є функції RSA, SQUARE і ЕХР, які визначають перестановки множин Zm, Qm і  (в позначеннях пункту 1.1). Нехай В — ядро функції f (відповідні предикати для перелічених функцій див. у пункті 1.3). Використовуючи f і В, сконструюємо генератор G з розширенням l(п), де функція l(п) обмежена деяким поліномом від n. Вважаємо, що Dn
(в позначеннях пункту 1.1). Нехай В — ядро функції f (відповідні предикати для перелічених функцій див. у пункті 1.3). Використовуючи f і В, сконструюємо генератор G з розширенням l(п), де функція l(п) обмежена деяким поліномом від n. Вважаємо, що Dn {0,1}n, і що належність до цієї множини можна ефективно розпізнати.
{0,1}n, і що належність до цієї множини можна ефективно розпізнати.
Вхід: паросток х0  {0,1}n.
{0,1}n.
· Якщо x0 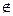 Dn, то зупинитись, інакше продовжувати.
Dn, то зупинитись, інакше продовжувати.
· Для і = 1,...,l(n) обчислити σі=В(хі-1) і хі = f(xi-1).
· Подати на вихід послідовність σ1σ2 ...σl(n)
Теорема 2.8.Для кожної важко оборотної перестановки f і її ядра В, описаний генератор G є псевдо випадковим.
Зауваження 2.9.Теорема говорить, що якщо паросток х0 вибирається рівно ймовірно з {0,1}n, то ніякий поліноміальний ймовірнісний алгоритм неспроможний відрізнити послідовність σ1σ2 ...σl від справжньої випадкової послідовності такої ж довжини. Насправді, це твердження залишається в силі, навіть коли оприлюднюється останній елемент хі, тобто, послідовність σ1σ2 ...σlхl не можна відрізнити за поліноміальний час від послідовності ρ1ρ2...ρlxl, де ρ1,...,ρl – випадкові і незалежні між собою біти. Зауважимо також, що хl є випадковим елементом множини Dn.
2.4. ЬЬS генератор.Окремо зупинимось на реалізації конструкції із попереднього пункту на основі функції Рабіна, яку ми позначаємо через SQUARE. Генератор, що виходить в результаті, називають генератором ЬЬS, де абревіатура утворена від імен її винахідників – Ленори Блюм, Мануїла Блюма та Майка Шуба. [77].
Нехай параметр l = l(n) обмежений поліномом від п. Щоб отримати із п випадкових бітів l псевдо випадкових, слід
· Вибрати випадково прості р та q такі, що 2п-1<m<2n для m=pq, і 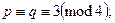
· Вибрати випадковий елемент 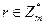 і обчислити x0=r2mod m;
і обчислити x0=r2mod m;
· Для і від 1 до il обчислювати
σі=xi-1mod 2, xi =  mod m;
mod m;
· Подати на вихід послідовність σ1σ2 ...σl.
Нескладно помітити, що ми притримувались загальної конструкції попереднього пункту із функцією f(x) = x2 mod m і її ядром, предикатом парності В(х) = x mod 2. Нагадаємо, що функція f не є біє-ктивною на Zm, але є такою на Qm. Саме тому в якості паростка ми вибирали x0 = r2 mod m — випадковий елемент множини Qm. За теоремою 2.8 ЬЬS генератор є псевдовипадковим, а отже, криптографічне надійним (за умови, що функція SQUARE справді є важкооборотною).
Приклад 2.10.Нехай р = 19 і q = 23. Тоді т = 233 отримуємо
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| xi | 101 | 150 | 213 | 358 | 123 | 271 | 25 | 188 | 384 | 187 | 9 | 81 | 6 |
| σi+1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
Деякі властивості генератора роблять його використання особливо зручним.
Твердження 2.11. За хі і простими р та q можна ефективно визначити всю послідовність x0,...,xl-1, а отже і послідовність σ1...σl;.
Зауважимо, що твердження не суперечить криптографічній надійності ЬЬS генератора, оскільки в застосуваннях прості р і q тримаються у таємниці.
Доведення. Припустимо, що відомо елемент xi, де 1 ≤ i ≤ l, і покажемо, як отримати xi-1. За бієктивністю функції f(x) = x2 mod m на Qm, елемент xi-1 однозначно визначається такими умовами
1) 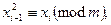
2) 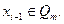
Введемо позначення у = xi-1 mod p і z = xi-1-imod q. За наслідком II.2.13 Китайської теореми про остачі, лишки у і z задовольняють умови

 (1)
(1)

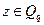 (2)
(2)
і, більше того, така пара y. Z однозначно визначає хі-1, причому ефективним чином.
Отже, досить знайти у та z. Для цього використаємо співвідношення
 та
та  (3)
(3)
З них безпосередньо видно, що у і z ефективно обчислюються із застосуванням бінарного методу піднесення до степеня.
Нам залишилося обгрунтувати рівності (3). Доведемо першу з них (для другої аргументи ідентичні). Досить перевірити умови (1) та (2) для у, заданого співвідношенням (3). Умова (2) негайно випливає із замкнутості Qp відносно множення. Умова (1) випливає з того, що добування кореня за модулем р таким, що р  3 (mod 4), еквівалентне піднесенню до степеня (р + 1)/4 — див. випадок 1 алгоритму з пункту IV.4.2.
3 (mod 4), еквівалентне піднесенню до степеня (р + 1)/4 — див. випадок 1 алгоритму з пункту IV.4.2.
Доведення завершено.
2.5. Потокові шифри. Потоковим називається шифр, який двійкове повідомлення М = m1m2,…,mi з використанням двійкового ключа такої ж довжини К = k1k2,...kl перетворює у криптотекст С = c1c2,…,cl шляхом покомпонентного додавання М і К за модулем 2: ci = (mi + ki) mod 2. Останнє прийнято записувати як  , а також
, а також  .
.
Різновиди потокових шифрів відрізняються між собою способом продукування ключа. У шифрі одноразового блокноту кожен біт ключа вибирається випадково і незалежно від інших бітів. Як зазначалося у пункті 1.3.2, за рахунок цього досягається абсолютна надійність шифру у теоретико-інформаційному сенсі, але ця ж обставина робить шифр одноразового блокноту непрактичним для довгих повідомлень.
Виходом може бути породження ключа К за допомогою криптографічно надійного генератора псевдовипадкових бітів (при цьому ключем варто називати не всю послідовність К, а лише паросток, що використовується при її генеруванні). Дамо опис конкретної реалізації цієї ідеї, яка використовує ЬЬS генератор,
Крипто Система Блюма-Гольдвассер [78]
Таємний ключ: р і q — великі прості числа, такі, що  .
.
Відкритий ключ m, де m = pq.
Шифрування. Щоб зашифрувати двійкове повідомлення М довжини l, Боб формує двійкову послідовність К = k1k2,...kl з l псевдовипадкових бітів, отриманих за допомогою ЬЬS генератора. Для цього він попередньо вибирає випадковий квадратичний лишок x0 за модулем m, послідовним піднесенням до квадрату отримує послідовність x0,...,xi  Qm, і покладає ki = x+i-1 mod 2. Далі Боб обчислює С = М
Qm, і покладає ki = x+i-1 mod 2. Далі Боб обчислює С = М К і посилає Алісі криптотекст, який складається з пари (С, хi). Зазначимо, що описане криптування є ймовірнісним, оскільки при різних виборах паростка для генерування псевдовипадкової послідовності К, повідомленню будуть відповідати різні криптотексти.
К і посилає Алісі криптотекст, який складається з пари (С, хi). Зазначимо, що описане криптування є ймовірнісним, оскільки при різних виборах паростка для генерування псевдовипадкової послідовності К, повідомленню будуть відповідати різні криптотексти.
Приклад 2.12. Нехай р = 19 і q = 23 — таємний ключ. Тоді відкритим ключем буде m = 437. Нехай потрібно закриптувати повідомлення НІ.1[2] Записуємо повідомлення у двійковій формі: М = 010001 001011. Запускаємо ЬЬS генератор, вибравши паросток r = 233. Ми потребуємо 12 псевдовипадкових бітів. Відповідні обчислення були проведені у прикладі 2.10. Маємо К = 101011 100111 і x12 = 6. Обчислюємо С = 111010 101100. Отже, криптотекстом буде пара (111010 101100, 6).
Дешифрування. Аліса, яка знає таємний ключ р і q, за числом xi обчислює всі члени послідовності x0,..,xl-1 (обчислення відбувається у зворотному порядку, як описано у доведенні твердження 2.11). На основі цієї послідовності Аліса відтворює двійковий вектор К і отримує М = С К.
К.
Ефективність. За швидкістю реалізацій криптосистема порівнянна із системою RSA. Вона також вигідно відрізняється від системи ймовірнісного криптування з пункту V.4.2 в такому плані. В останній криптосистемі розмір криптотексту більший від розміру повідомлення у кількість разів, що дорівнює довжині ключа, в той час як у системі Блюма-Гольдвассер криптотекст довший від повідомлення лише на довжину ключа.
Надійність. Доведено, що система є надійною за умови важкості факторизації цілих Блюма. Один із варіантів відповідної теореми звучить так. Для будь-якого повідомлення М довжини l = (logm)O(1), випадкову величину (С, xl) неможливо відрізнити від величини (ρ1…ρl,х), що складається із справжньої випадкової двійкової послідовності ρ1…ρl і випадкового квадратичного лишка х  Qm, ніякою схемою поліноміального від l розміру (див. вправу 2.2). Доведення є нескладною комбінацією неоднорідної версії теореми 2.8 (див. також зауваження 2.9) та результатів про ядро функції Рабіна в [77, 67] (див. вправу 1.2). Зауважимо, що криптосистема із щойно сформулюваною умовою надійності є надійною в сенсі означення V.4.I.
Qm, ніякою схемою поліноміального від l розміру (див. вправу 2.2). Доведення є нескладною комбінацією неоднорідної версії теореми 2.8 (див. також зауваження 2.9) та результатів про ядро функції Рабіна в [77, 67] (див. вправу 1.2). Зауважимо, що криптосистема із щойно сформулюваною умовою надійності є надійною в сенсі означення V.4.I.
ВПРАВИ
2.1. Нехай с > 1 — ціла константа. Припустимо, що G — псевдовипадковий генератор з розширенням п + 1. Довести, що тоді псевдо випадковим є також генератор G' з розширенням nd, який задається співвідношенням G'(x) = σ1…σnd для х  {0,1}n, де σiхі = G(xi-1) і xо = х.
{0,1}n, де σiхі = G(xi-1) і xо = х.
2.2. Модифікуємо означення 2.2 нерозрізнюваності ансамблів, замінивши у ньому алгоритм А на послідовність функціональних схем Сп (див.пункт III.2.3). При цьому розглядаємо такі послідовності, що схема Сп обчислює деяку булеву функцію f: {0, 1}n —> {0,1}, і розмір схеми Сп обмежений деяким поліномом від п. Ансамблі {Xn}n N і {Yn}n
N і {Yn}n N будемо називати поліноміально нерозрізнюваними, якщо для будь-якої такої послідовності схем {Cn}n
N будемо називати поліноміально нерозрізнюваними, якщо для будь-якої такої послідовності схем {Cn}n N поліноміального розміру
N поліноміального розміру
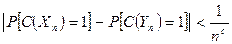
для довільної константи с при досить великих п. Нове означення будемо називати неоднорідним, а "старе" означення 2.2 — однорідним (про поняття неоднорідності див. пункт III.2.3).
Довести, що неоднорідне означення сильніше за однорідне: якщо ансамблі поліноміально нерозрізнювані в неоднорідному сенсі, то вони поліноміально нерозрізнювані і в однорідному сенсі. Як наслідок, генератор, псевдовипад-ковий при неоднорідному означенні нерозрізнюваності, є псевдовипадковим і при однорідному означенні.
2.3.Нехай поліноміальний імовірнісний алгоритм розв'язує задачу обчислення з ймовірністю помилки е, використовуючи на входах довжини п випадкову послідовність довжини nd. Припустимо тепер, що замість справжньої випадкової послідовності використовується отримана із випадкового паростка довжини п послідовність такої ж довжини, псевдовипадкова у сенсі неоднорідного означення із попередньої вправи. Довести, що для досить довгих входів ймовірність помилки може зрости щонайбільше на 1/пс, для довільної наперед заданої константи с.
2.4.Довести теорему 2.7.
2.5.Для генератора G: {0,1)т —> {0,1}l(n) позначимо через Zl(n) випадкову величину G(x) зі значеннями в {0,1}l(n), де х рівномірно розподілений на {0,1}n. Припустимо, що ансамбль {Zl(n)}п N непередбачуваний, тобто, знаючи попередні біти послідовності Zl(n), черговий біт неможливо передбачити у сенсі означення 2.6. Довести, що тоді у такому ж сенсі, знаючи лише кінцевий відрізок бітів, неможливо вгадати попередній до них біт.
N непередбачуваний, тобто, знаючи попередні біти послідовності Zl(n), черговий біт неможливо передбачити у сенсі означення 2.6. Довести, що тоді у такому ж сенсі, знаючи лише кінцевий відрізок бітів, неможливо вгадати попередній до них біт.
2.6.Довести теорему 2.8 в такий спосіб. Припустити, що G не витримує тестування наступного біту і виснувати звідси, що В(х) можна ефективно отримати за f(x) з ймовірністю, переважаючою 1/2 + 1/пс для деякої константи с.
2.7.Сконструювати псевдовипадковий генератор, застосувавши загальну конструкцію пункту 2.3 до важкооборотної перестановки a) RSA, ь)ЕХР.
2.8. Довести, що в позначеннях з опису ЬЬS генератора,

де ф(m) = (р - 1)(q - 1).
2.9. Використовується криптосистема Блюма-Гольдвассер з таємним ключем р = 19 і q = 23.
a) Обчислити відкритий ключ і зашифрувати повідомлення ТАК. При генеруванні псевдовипадкової послідовності використати паросток 250.
b) Дешифрувати криптотекст (111101 111111, 73).
ЛІТЕРАТУРА
Фізичні способи отримання випадкових послідовностей описані у [137]. Деякі добре відомі генератори псевдовипадкових чисел з успіхом використовуються на практиці у алгоритмах Монте Карло (див. [24, § 2 розділу 8] та [32, розділ 3]). На жаль, ці генератори непридатні для криптографічних застосувань, оскільки не є криптографічне надійними. Прикладом може служити лінійний генератор, який на основі випадкового паростка x0  Zm породжує послідовність хо,х1,x2,... згідно із рекурентним співвідношенням xi = (ахі-1 + ь) mod m. У [125] показано, що суперник, грунтуючись лише на кількох членах послідовності x0,x1,x2,… може визначити параметри а, ь, і m, і таким чином отримати будь-який член послідовності (див. також [10]). Як показано в [109], послідовність, що є розкладом у нескінченний двійковий дріб будь-якого алгебраїчного числа, на зразок
Zm породжує послідовність хо,х1,x2,... згідно із рекурентним співвідношенням xi = (ахі-1 + ь) mod m. У [125] показано, що суперник, грунтуючись лише на кількох членах послідовності x0,x1,x2,… може визначити параметри а, ь, і m, і таким чином отримати будь-який член послідовності (див. також [10]). Як показано в [109], послідовність, що є розкладом у нескінченний двійковий дріб будь-якого алгебраїчного числа, на зразок 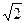 = 1,011010100..., також є криптографічно ненадійною.
= 1,011010100..., також є криптографічно ненадійною.
Теореми 2.7 та 2.8 доведено в [150] та [79], відповідно. В останній роботі загальну конструкцію псевдовипадкового генератора було реалізовано для важкооборотної перестановки ЕХР. Доведення підсилення теореми 2.8, згаданого у зауваженні 2.9, можна знайти в [93, твердження 3.17].
Конструкцію псевдовипадкового генератора на основі довільної важкооборотної функції (не обов'язково перестановки) розроблено в [107, 103]. Таким чином, існування псевдовипадкових генераторів випливає з існування важкооборотних функцій. Обернене твердження встановлюється просто (деталі в [93]).
У [94, 117] показано як маючи генератор псевдовипадкових бітів, отримати симетричну криптосистему, надійність якої можна формально довести.
ЛЕКЦІЯ 19
Читайте також:
- Асинхронні виконавчі двигуни і тахогенератори
- Асинхронні генератори
- Блокінг-генератори.
- Генератори імпульсів
- Генератори імпульсних сигналів
- Генератори постійного струму
- Генератори постійного струму, класифікація, характеристики, особливості.
- Охолоджувачі напоїв, льодогенератори і фризери
- Поглинання, спонтанне і вимушене випромінювання. Квантові генератори
- Синхронні двигуни і генератори.
- Універсальні генератори
| <== попередня сторінка | | | наступна сторінка ==> |
| Важкооборотні функції | | | Обмін ключем |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |