
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Геодезичних вимірів
Завершальною процедурою зрівнювання геодезичних вимірів параметричним способом, як це відомо|показний| із попереднього підрозділу, є оцінка точності зрівняних|урівнювати| значень невідомих. Розглянемо|розглядуватимемо| цю процедуру детально. Як і в математичній обробці однієї величини оцінюватимемо точність декількох невідомих, тобто визначимо їх середні квадратичні похибки|  . Розв’язання даної задачі має деякі особливості, що полягають в тому, що поправки
. Розв’язання даної задачі має деякі особливості, що полягають в тому, що поправки 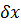 ,
, 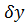 ,
, 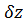 , …,
, …,  , – величини залежні. Причому математичному аналізу піддається не одна функція, а декілька.
, – величини залежні. Причому математичному аналізу піддається не одна функція, а декілька.
Оскільки величини 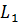 ,
, 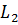 ,…,
,…, 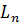 (див. п.п. 10.1) виміряні|виміряти| незалежно і рівноточно|, їх середні квадратичні похибки| дорівнюють
(див. п.п. 10.1) виміряні|виміряти| незалежно і рівноточно|, їх середні квадратичні похибки| дорівнюють
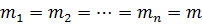 .
.
Відповідно будуть рівні і їх ваги 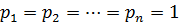 , а також середні квадратичні похибки вимірів m і середні квадратичні похибки одиниць ваги μ,
, а також середні квадратичні похибки вимірів m і середні квадратичні похибки одиниць ваги μ, 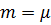 .
.
Звернемося до рівняння (10.18), де елементи матриць Δ і λ є змінними, а елементами зворотної матриці 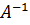 є безперервні функції (10.10), що диференціюються, і відповідно до основної теореми теорії похибок (див. п.п.4.1) характеризуються стандартами даних функцій. Тоді зворотна матриця
є безперервні функції (10.10), що диференціюються, і відповідно до основної теореми теорії похибок (див. п.п.4.1) характеризуються стандартами даних функцій. Тоді зворотна матриця 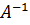 може бути представлена функціональним визначником матриці Якобі (Якобіаном), елементи якого, є часткові похідні.
може бути представлена функціональним визначником матриці Якобі (Якобіаном), елементи якого, є часткові похідні.
Запишемо:
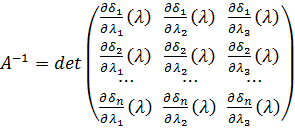 . (10.19)
. (10.19)
Підставимо отриману матрицю (10.19), а також матриці Δ і λ у вираз (10.18) і враховуючи властивості операцій над матрицями отримаємо наступне співвідношення:
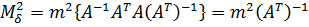 .
.
Спрощуючи отриману|одержувати| формулу матимемо:
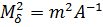 .(10.20)
.(10.20)
Отримана|одержувати| і записана в матричному вигляді формула для розрахунку середньої квадратичної похибки| сукупності поправок за умови рівноточних| вимірів і незалежності поправок 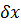 ,
, 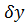 ,
, 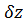 , …,
, …,  .
.
Для обчислення точності зрівняних значень невідомих у разі їх залежності виконаємо наступні процедури. Враховуючи, що матриця 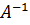 симетрична, замінимо в ній діагональніелементи на вагові коефіцієнти, величини яких дорівнюють зворотним вагам невідомих
симетрична, замінимо в ній діагональніелементи на вагові коефіцієнти, величини яких дорівнюють зворотним вагам невідомих
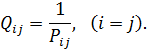
Відмітимо, що діагональні елементи формованої матриці Qзавжди позитивні. Недіагональні елементи 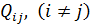 можуть бути як позитивними, так і негативними. Вони є кореляційними моментами, обумовленими залежністю певних невідомих. Наприклад, елемент
можуть бути як позитивними, так і негативними. Вони є кореляційними моментами, обумовленими залежністю певних невідомих. Наприклад, елемент 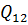 і рівний йому елемент
і рівний йому елемент 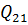 слід розглядати як кореляційний момент, обумовлений залежністю величин x і у, тобто
слід розглядати як кореляційний момент, обумовлений залежністю величин x і у, тобто 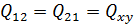 .
.
Позитивне значення 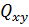 свідчить про те, що збільшення або зменшення похибки
свідчить про те, що збільшення або зменшення похибки  неминуче приводить до збільшення або зменшення величини
неминуче приводить до збільшення або зменшення величини 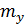 . І, навпаки, негативне значення
. І, навпаки, негативне значення 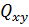 свідчить про те, що збільшення
свідчить про те, що збільшення  тягне за собою зменшення
тягне за собою зменшення 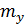 , а зменшення
, а зменшення  – збільшення
– збільшення 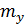 .
.
Тоді справедливо записати, що,і 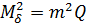 .У розгорненому вигляді формула (10.20) набере вигляду
.У розгорненому вигляді формула (10.20) набере вигляду
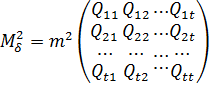 . (10.21)
. (10.21)
Звідси витікає, що квадрат середньої квадратичної похибки сукупності невідомих x, у, z,…, t є матрицею, яка отримана множенням квадрата середньої квадратичної похибки m виміряних величин  на матрицю Q.
на матрицю Q.
При обчисленні середніх квадратичних похибок невідомих x, у, z,…, t враховуватимемо, що ваги функцій результатів вимірів пов'язані із стандартом і стандартом одиниці ваги співвідношенням (6.8). Тоді справедливо записати наступні співвідношення:
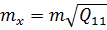 ,
, 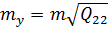 ,…,
,…,  . (10.22)
. (10.22)
З проведеного аналізу виходить, що хоча величини  виміряні рівноточно і незалежно, отримані в результаті зрівнювання значення незалежних величин x, у, z,…, t є нерівноточними і залежними величинами.
виміряні рівноточно і незалежно, отримані в результаті зрівнювання значення незалежних величин x, у, z,…, t є нерівноточними і залежними величинами.
Приклад|зразок| 10.1.
Якщо шуканими невідомими є координати x, y пунктів геодезичної мережі, то сукупна похибка положення пункту в даній системі координат відповідно до виразу (10.21) характеризується матрицею:
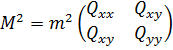 . (10.23)
. (10.23)
Отримана|одержувати| формула дає можливість|спроможність| розрахувати наступні точності| характеристики положення|становища| точки|точки| на площині|площині|:
1. Середні квадратичні похибки по осях координат  і
і 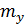 , обчислювані за формулами (10.22). Вони залежать від вибору системи координат (рис. 10.1).
, обчислювані за формулами (10.22). Вони залежать від вибору системи координат (рис. 10.1).
2. Кругову середню квадратичну похибку|, обчислювану за формулою:
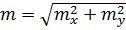 , (10.24)
, (10.24)
яка знайшла широке застосування|вживання| в геодезичній практиці, при цьому виходячи з припущення|гадки|, що розсіювання вимірів по осях X і Y має однакову ймовірність.
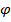
|
| b |
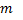
|
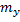
|
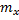
|
| P |
| a |
| U |
| X |
| Y |
| V |
Рис. 10.1 – Ілюстрація для прикладу|приміром| 10.1
3. Еліпс похибок, орієнтація і розміри осей якого визначають найбільш вірогідні напрями|направлення| і величину максимальної і мінімальної середньої квадратичної похибки| положення геодезичного пункту.
Для визначення сукупної похибки положення геодезичного пункту скористаємося співвідношенням (10.23) і рис. 10.1, де показано, що поворотом осей навколо точки Р можна підібрати таку систему координат UV, при якій недіагональні елементи матриці Qдорівнюватимуть нулю і даний вираз матиме вигляд:
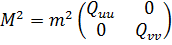 . (10.25)
. (10.25)
Необхідний для такого перетворення кут|ріг| повороту осей обчислюється за формулою:

а елементи 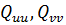 на основі рівнянь:
на основі рівнянь:

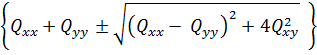 .
.
Велика і мала піввісь еліпса похибок будуть відповідно дорівнювати:
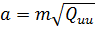 ,
, 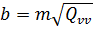 . (10.27)
. (10.27)
Таким чином, детально розглянута|розглядувати| процедура (див. п.п.10.3 процедура 12) оцінювання точності зрівняних|урівнювати| значень невідомих. На прикладі|зразку| демонструється послідовність обчислення точнісних|підрахунку| |характеристик.
10.5. Обчислення|підрахунок| емпіричної середньої квадратичної похибки|
за поправками, одержаними|одержувати| із|із| зрівнювання.
Як правило, виміряні величини 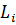 визначені за умови:
визначені за умови:
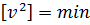 ,
,
тобто є підстава припускати, що на їх основі можна отримати спроможну і незміщену оцінку середньої квадратичної похибки m. Проте, на підставі цієї ж умови і здорового глузду можна стверджувати, що сума квадратів дійсних похибок завжди буде більша суми квадратів отриманих поправок. Тоді справедлива нерівність 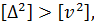 де Δ – дійсні похибки. Розділивши цю нерівність на n, отримаємо:
де Δ – дійсні похибки. Розділивши цю нерівність на n, отримаємо:
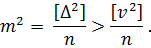
Отже, величина 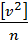 буде спроможною, але зміщеною оцінкою m. Для того, щоб вона виявилася незміщеною, необхідно знаменник правої частини зменшити на деяку, поки невідому, величину u.
буде спроможною, але зміщеною оцінкою m. Для того, щоб вона виявилася незміщеною, необхідно знаменник правої частини зменшити на деяку, поки невідому, величину u.
Тоді справедливо записати емпіричну середню квадратичну похибку в наступному вигляді:

В даному випадку, задача зводиться до визначення невідомої величини u.
Проаналізуємо вираз (10.28) і перш за все, відзначимо, що загальне число вимірів n не може бути менше числа необхідних вимірів, тобто 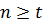 . Звідси витікає, що u не може бути більше t, оскільки при
. Звідси витікає, що u не може бути більше t, оскільки при 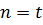 знаменник у формулі (10.28) дорівнюватиме нулю. Отже
знаменник у формулі (10.28) дорівнюватиме нулю. Отже 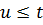 .
.
Зробимо припущення, що 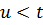 . При
. При 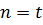 завдання зрівнювання не виникає, поправки
завдання зрівнювання не виникає, поправки 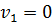 ,
, 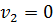 ,…,
,…, 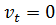 , отже і
, отже і 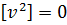 , що суперечить здоровому глузду, оскільки
, що суперечить здоровому глузду, оскільки 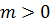 .
.
Це дає підставу,|основу| формулу (10.28) записати у виді:

Наведений доказ рівності (10.29) заснований на припущеннях і евристичних міркуваннях тому не є|з'являється| суворим|суворим|. Існує і строгий|суворий| доказ, який є громіздким і в теперішньому курсі не розглядається|розглядує|.
З тієї причини, що емпірична середня квадратична похибка| m найчастіше визначається із невеликої кількості вимірів, її надійність визначає середня квадратична похибка, яка обчислюється за формулою:

Таким чином, на основі умов мінімізації суми квадратів поправок розглянутий|розглядувати| наближений спосіб оцінювання їх точності за результатами зрівнювання.
10.6. Середня квадратична похибка виміряних|виміряти| величин
після|потім| зрівнювання
У попередньому підрозділі знайдено| співвідношення (10.28), яке дозволяє оцінювати значення середньої квадратичної похибки| m виміряних|виміряти| величин до зрівнювання. Виникає справедливе питання. Чи зміниться ця величина після|потім| зрівнювання?
Щоб|аби| відповісти на це питання приведемо доведення теореми відоме з|із| теорії похибок.
Теорема 10.1. Середнє значення відношення квадрата середньої квадратичної похибки після зрівнювання до квадрата середньої квадратичної похибки до зрівнювання, тобто її середнє зменшення, обумовлене зрівнюванням системи виміряних величин способом найменших квадратів, дорівнює відношенню числа необхідних вимірів до всіх вимірів, тобто:

де 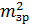 – середня квадратична похибка виміряних величин після зрівнювання, t – число необхідних вимірів, n – число всіх вимірів.
– середня квадратична похибка виміряних величин після зрівнювання, t – число необхідних вимірів, n – число всіх вимірів.
Доказ
Для зручності і простоти доведення теореми запроваджуватимемо обмеження на кількість невідомих. Вважатимемо|гадатимемо|, що система лінеаризованих рівнянь поправок (10.7) містить|утримує| три невідомих і n рівнянь. Тоді в матричному вигляді систему рівнянь поправок можна записати наступним чином|виді|:
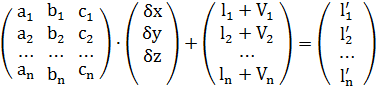 ,(10.32)
,(10.32)
де, 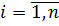 – зрівняні значення вільних членів.
– зрівняні значення вільних членів.
Представимо|уявлятимемо| співвідношення|ставлення| (2.31) у виді:
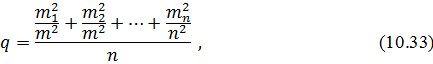
де 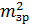 =
= 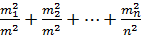 .
.
Значення 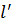 – функції поправок
– функції поправок 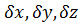 . Знайдемо формульні співвідношення доданків
. Знайдемо формульні співвідношення доданків 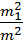 ,
, 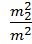 ,
, 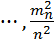 формули (10.33). Для цього продиференціюємо початкові рівняння поправок (10.7) по змінних
формули (10.33). Для цього продиференціюємо початкові рівняння поправок (10.7) по змінних 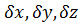 і враховуючи результати доведення основної теореми похибок і раніше отримані формули (10.19) і (10.20) представимо середні квадратичні похибки у вигляді добутку Якобіанів:
і враховуючи результати доведення основної теореми похибок і раніше отримані формули (10.19) і (10.20) представимо середні квадратичні похибки у вигляді добутку Якобіанів:
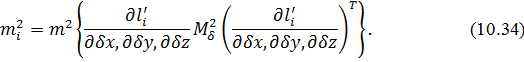
Розділимо праву і ліву частину отриманого рівняння на 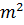 і проведемо необхідні операції з Якобіанами. Крім того, враховуючи рівноточність вимірів отримаємо:
і проведемо необхідні операції з Якобіанами. Крім того, враховуючи рівноточність вимірів отримаємо:
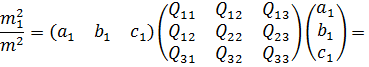
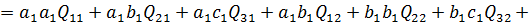
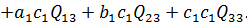 (a)
(a)
Аналогічно, для 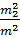 ,
, 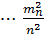 отримаємо:
отримаємо:
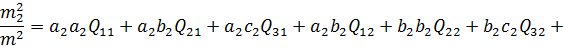
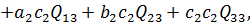 (b)
(b)
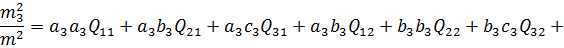
 (c)
(c)

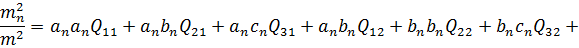
 (d)
(d)
Підставляючи (а), (b), (c) і (d) у формулу (10.33) підсумуємо добутки 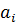 ,
, 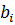 ,
,  виносячи за дужки вагові коефіцієнти
виносячи за дужки вагові коефіцієнти 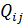 . В результаті знайдемо шукане значення:
. В результаті знайдемо шукане значення:
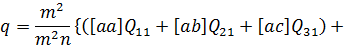
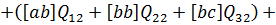 (10.35)
(10.35)
 .
.
Із властивостей операцій над матрицями в лінійній алгебрі відомо, що
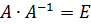 ,
,
де Е – одинична матриця, у якої діагональні елементи дорівнюють 1, а недіагональні – 0. У формулі (10.35) суми добутків в круглих дужках, враховуючи (10.13) і (10.21) є добутками i-го рядка матриці Ана i-й стовпець матриці 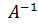 .Отже, вони відповідають діагональним елементам матриці Е, які дорівнюють 1. Тоді на підставі (10.31), (10.33) і (10.35) можна записати:
.Отже, вони відповідають діагональним елементам матриці Е, які дорівнюють 1. Тоді на підставі (10.31), (10.33) і (10.35) можна записати:
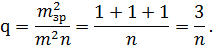
При трьох невідомих 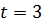 і поширюючи отриману рівність на будь-яке число невідомих, остаточно отримаємо:
і поширюючи отриману рівність на будь-яке число невідомих, остаточно отримаємо:

що і потрібно було довести (див. формулу 10.31).
Таким чином, зрівнювання методом найменших квадратів підвищує в середньому точність результатів вимірів.
10.7. Зрівнювання і оцінка точності при нерівноточних| вимірах|вимірах|
У попередньому підрозділі розглядалася оцінка точності тільки рівноточних вимірів. Відомо, що у разі нерівноточних вимірів точність виміряних величин 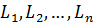 характеризується вагами
характеризується вагами 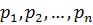 . Отже, і вільні члени в рівняннях поправок:
. Отже, і вільні члени в рівняннях поправок:
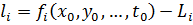 ,
,
що є функціями виміряних величин, також матимуть ваги 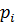 .
.
Зрівнювання результатів вимірів проводитимемо з урахуванням умов: 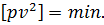 Розглянемо деяку функцію
Розглянемо деяку функцію 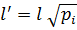 . Згідно тверджень, зроблених в п.п. 6.2 вагу цієї функції можна прирівняти до 1
. Згідно тверджень, зроблених в п.п. 6.2 вагу цієї функції можна прирівняти до 1
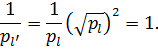
Отже, оскільки 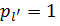 у цьому випадку нерівноточні вимірювання можна звести до рівноточних. Для цього достатньо кожне рівняння системи поправок помножити на
у цьому випадку нерівноточні вимірювання можна звести до рівноточних. Для цього достатньо кожне рівняння системи поправок помножити на 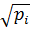 , тобто систему лінійних рівнянь поправок можна записати у загальному вигляді:
, тобто систему лінійних рівнянь поправок можна записати у загальному вигляді:
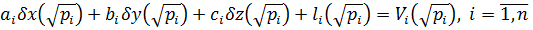 .
.
Запишемо цю систему рівнянь в матричному вигляді|виді|:
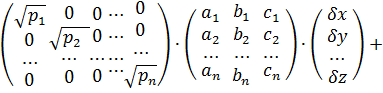
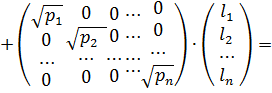
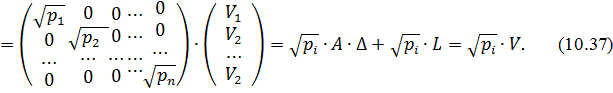
З метою звільнення від знаку радикала, а також перетворення формули (10.37) до виду нормальних рівнянь помножимо її праву і ліву частини на добуток 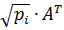 . Отримаємо:
. Отримаємо:
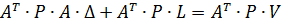 ,(10.38)
,(10.38)
де
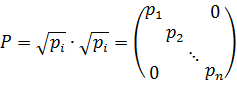 .
.
Спростимо формулу (10.38). Для цього позначимо матрицю коефіцієнтів нормальних рівнянь:
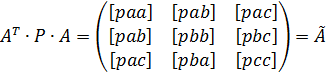 . (10.39)
. (10.39)
Вектор-стовпець | вільних членів нормальних рівнянь позначимо:
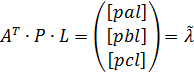 . (10.40)
. (10.40)
Для дотримання умов побудови нормальних рівнянь вектор-стовпець 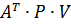 прирівняємо до нуля. Отримаємо:
прирівняємо до нуля. Отримаємо:
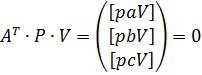 . (10.41)
. (10.41)
З введеними|запроваджувати| позначеннями система нормальних рівнянь набуде вигляду:
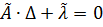 . (10.42)
. (10.42)
Отримане матричне рівняння як і у разі рівноточних вимірів, вирішується шляхом множення його зліва на зворотну матрицю:
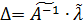 . (10.43)
. (10.43)
При нерівноточних вимірах аналогічно вирішується і завдання оцінки точності невідомих 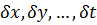 з використанням формули:
з використанням формули:
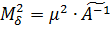 .
.
Емпірична середня квадратична похибка |одиниці ваги обчислюється за формулою:

Таким чином, видно|показний|, що зрівнювання нерівноточних| вимірів|вимірів| принципово не відрізняється від зрівнювання рівноточних вимірів|вимірів||.
10.8. Приклади|зразки| складання рівнянь поправок для різних
видів геодезичних вимірів|вимірів| і мереж|сітей|
Приклад|зразок| зрівнювання вимірів|вимірів| при побудові|шикуванні| геодезичної мережі|сіті|
методом тріангуляції
Прийнято вважати що метод тріангуляції винайшов і вперше|уперше| застосував голландський астроном і математик, професор Лейденського університету Снелліус Віллеброд в 1615–17 рр.
Для геодезичних побудов|шикувань|, на сьогоднішній день|нині| використовується наступне|таке| визначення терміну «тріангуляція».
| <== попередня сторінка | | | наступна сторінка ==> |
| Розв'язання нормальних рівнянь | | | Визначення 10.1. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |