Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Закон збереження механічної енергії

Механічною енергією, або повною механічною енергією, називається енергія механічного руху та взаємодії. Механічна енергія системи матеріальних точок дорівнює сумі їх кінетичної енергії і потенціальної енергії взаємодії цих точок одна з іншою та з зовнішніми тілами:

Елементарний приріст механічної енергії системи за малий проміжок часу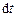

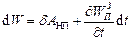де – алгебраїчна сума елементарних робіт, виконуваних за час 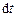усіма діючими на систему внутрішніми та зовнішніми непотенціальними силами. Доданок являє собою зміну за час 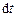потенціальної енергії системи і відповідно її повної механічної енергії, зумовлену нестаціонарністю зовнішніх потенціальних сил.

Якщо на систему матеріальних точок діють лише консервативні сили, то і . Відповідно, повна механічна енергія такої системи зберігається , тобто справедливим є закон, який називається законом збереження механічної енергії: при русі системи матеріальних точок, на які діють лише консервативні (і гіроскопічні) сили, її механічна енергія не змінюється.

Зокрема, цей закон справедливий для замкнених консервативних систем: механічна енергія замкненої системи не змінюється з часом, якщо всі внутрішні сили, які діють у цій системі, потенціальні або не виконують роботи.

Закон збереження механічної енергії пов¢язаний із однорідністю часу. Ця властивість часу проявляється в тому, що закони руху замкненої системи (або системи, що знаходиться в стаціонарному зовнішньому полі) не залежать від вибору початку відліку часу. Наприклад, при вільному падінні тіла в стаціонарному потенціальному полі сили тяжіння біля поверхні Землі, швидкість тіла і пройдений ним шлях залежать лише від тривалості вільного падіння тіла і від початкової швидкості, а не від того, в який конкретно момент часу тіло почало падати.

Механічна енергія замкненої неконсервативної системи змінюється за рахунок роботи, виконуваної всіма непотенціальними внутрішніми силами . Гіроскопічні сили роботи не виконують і внеску в не дають, тобто існування таких сил в системі не призводить до зміни її механічної енергії.

Дія дисипативних сил – наприклад, сил тертя – призводить до поступового зменшення механічної енергії замкненої системи. Цей процес називається дисипацією енергії. Відповідно система, механічна енергія якої неперервно зменшується з часом, називається дисипативною системою. При дисипації енергії відбувається перетворення механічної енергії системи в інші види енергії (наприклад, в енергію безладного руху молекул).

Перетворення механічної енергії здійснюється у повній відповідності до загального закону природи – закону збереження енергії. Згідно з цим законом, енергія може переходити з однієї форми в іншу і перерозподілятися всередині системи, але її загальна кількість у замкненій системі повинна залишатися постійною. Із закону збереження та перетворення енергії випливає, що зміна енергії незамкненої системи, що відбувається при взаємодії системи з зовнішнім середовищем (зовнішніми тілами та полями), повинна бути чисельно рівною і протилежною за знаком зміні енергії зовнішнього середовища. Іншими словами, зміна енергії системи при її взаємодії з зовнішнім середовищем повинна дорівнювати тій енергії, яку система отримує ззовні.

У всіх реальних механічних системах діють сили опору і тертя, внаслідок чого всі ці системи неконсервативні. Проте в деяких випадках їх можна наближено вважати консервативними і застосовувати до них закон збереження механічної енергії. Такий підхід можливий, якщо в розглядуваному процесі робота всіх непотенціальних сил, які діють на систему, нехтовно мала порівняно з механічною енергією системи , тобто , так що 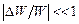, де – зміна механічної енергії системи.

Станом механічної рівноваги системи називається такий стан, із якого вона може бути виведена тільки в результаті зовнішньої силової дії. У цьому стані всі матеріальні точки системи перебувають у спокої, так що кінетична енергія системи дорівнює нулю. Стан механічної рівноваги називають стійким, якщо малий зовнішній вплив на систему спричиняє малу зміну її стану. При цьому в системі виникають сили, які прагнуть повернути систему в стан рівноваги. Стан механічної рівноваги називають нестійким, якщо система при як завгодно малому зовнішньому впливові виходить із цього стану і більше не повертається в нього. При цьому виникають сили, які спричиняють подальше відхиляння системи від стану рівноваги.

Закон збереження механічної енергії дозволяє вказати умови рівноваги консервативних систем: у станах стійкої рівноваги потенціальна енергія системи має мінімуми, а в станах нестійкої рівноваги – максимуми.

На основі закону збереження механічної енергії можна з¢ясувати, якою є область можливих конфігурацій консервативної системи. Кінетична енергія системи 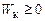. Тому при заданому значенні механічної енергії системи остання може знаходитися тільки в таких станах, які задовольняють умову: . Рис. 3.5 відповідає найпростішому випадку, коли матеріальна точка здійснює одновимірний рух уздовж осі ОХ у зовнішньому стаціонарному полі. Потенціальна енергія точки є функцією лише одної координати х, тобто 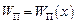. Графік цієї залежності, показаний на рис.3.5, називається потенціальною кривою. При фіксованому значенні механічної енергії матеріальної точки, показаному на рис. 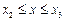3.5, точка може рухатися, залишаючись в одній із таких трьох областей: (область І), (область ІІІ), (область V). Вони відділені одна від іншої областями ІІ і ІV так званих потенціальних бар¢єрів aeb і cgd, у межах яких матеріальна точка знаходитися не може. На межах потенціальних бар¢єрів (у точках a, b, c, і d) матеріальна точка змінює напрямок свого руху на протилежний, причому в області І точка може необмежено віддалятися ліворуч від межі бар¢єру, а в області V – праворуч від межі a бар¢єру. В області ІІІ матеріальна точка коливається між точками b і c – вона знаходиться в так званій потенціальній ямі bfc.

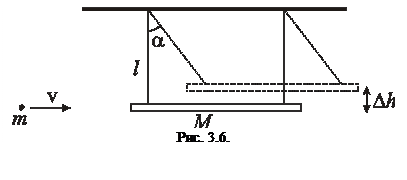Приклад застосування законів збереження енергії і імпульса.

Розглянемо один з варіантів так званого балістичного маятника (рис.3.6). Тіло маси підвішене на двох однакових нитках довжиною . Куля маси 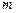летіла горизонтально, потрапила у тіло і застрягла в ньому. У результаті нитки відхилились на максимальний кут 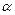, який легко можна виміряти на експерименті. Розглянемо, як за результатами вимірювання кута 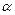можна визначити швидкість кулі 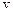. Для спрощення формул одразу припустимо, що . Нехай куля і тіло у даній задачі утворюють механічну систему, до якої ми спробуємо застосувати закони збереження імпульсу і енергії. Запишемо імпульс і механічну енергію системи у три такі моменти часу: 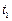- момент безпосередньо перед ударом кулі, 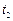- момент безпосередньо після удару кулі, коли куля вже застрягла, але масивне тіло ще не встигло відхилитись від положення рівноваги, 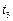- момент максимального відхилення тіла від положення рівноваги. У цій задачі ми будемо розглядати лише горизонтальну складову імпульса системи.

У момент 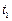імпульс системи 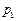(сума імпульсів кулі і тіла) і механічна енергія системи дорівнюють

, .

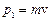При цьому потенціальна енергія кулі і тіла у полі тяжіння до Землі до співудару вважається такою, що дорівнює нулю.

У момент 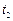тіло із застряглою кулею отримало імпульс і почало рухатися з якоюсь швидкістю . Тоді імпульс і енергія у цей момент дорівнюють

, .

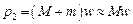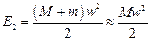У момент максимального відхилення 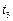тіло зупиняється

, .

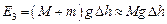Строго кажучи, розглядувана система не є замкненою. На неї діють зовнішні сили – сили тяжіння до Землі і сили реакції підвісу. Але, незважаючи на це, ми зможемо застосувати закони збереження енергії та імпульса. Дійсно, на етапі зовнішні сили спрямовані вертикально і не впливають на розглядувану горизонтальну складову імпульсу. Отже, можна записати

, або .

Що стосується енергії, то на проміжку під час гальмування кулі всередині тіла відбувається перетворення частини кінетичної енергії кулі в інші форми енергії, наприклад, у теплову. Отже, .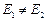

На відрізку 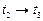зовнішні сили реакції підвісу змінюються, у них з’являється горизонтальна складова, отже на цьому відрізку імпульс системи не зберігається, тобто . Тут відбувається перетворення кінетичної енергії системи у потенціальну, отже

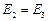, або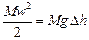

З отриманих співвідношень шляхом нескладних алгебраїчних перетворень можна отримати шукану величину 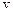. З геометричних міркувань очевидно

Тоді отримаємо

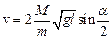<== попередня сторінка	\|	наступна сторінка ==>
Потенціальна енергія	\|	Абсолютно пружний і непружний удари

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.